22.8: Aplicaciones
- Page ID
- 161312
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El método de cinco pasos
Ahora estamos en condiciones de estudiar algunas aplicaciones de ecuaciones racionales. Algunos de estos problemas tendrán aplicaciones prácticas mientras que otros están pensados como desarrolladores de lógica.
Aplicaremos el método de cinco pasos para resolver problemas de palabras.
Método de cinco pasos
- Representar todas las cantidades desconocidas en términos de x o alguna otra letra.
- Traducir las frases verbales a símbolos matemáticos y formar una ecuación.
- Resuelve esta ecuación.
- Verifique la solución sustituyendo el resultado en la declaración original del problema.
- Escribe la conclusión.
Recuerda, el paso 1 es muy importante: siempre
Introducir una variable.
Conjunto de Muestras A
Cuando se suma el mismo número al numeartor y denominador de la fracción\(\dfrac{3}{5}\), el resultado si\(\dfrac{7}{9}\). ¿Cuál es el número que se agrega?
Paso 1: Deja que\(x = \) se agregue el número.
\ (\ begin {array} {vaciado a la izquierda}
\ text {Paso 2:} &\ dfrac {3+x} {5+x} &=\ dfrac {7} {9}
\\ text {Paso 3:} &\ dfrac {3+x} {5+x} &=\ dfrac {7} {9} &\ text {Un valor excluido es} -5\
&&&\ text {Multiplica cada término por} 9 (5 + x)\\
& 9 (5 + x)\ cdot\ dfrac {3 + x} {5 + x} &= 9 (5 + x)\ cdot\ dfrac {7} {9}\\
& 9 (3 + x) &= 7 (5 + x)\\
& 27 + 9x &= 35 + 7x\\
& 2x &=8\\
& x &= 4 &\ text {Comprueba esta solución potencial}\\
\ text {Paso 4:} &\ dfrac {3 + 4} {5 + 4} &=\ dfrac {7} {9} &\ text {Sí, esto es correcto}\\
\ text {Paso 5: El número agregado es} 4
\ end {array}\)
Conjunto de práctica A
El mismo número se suma al numerador y denominador de la fracción\(\dfrac{4}{9}\). El resultado es\(\dfrac{2}{3}\). ¿Cuál es el número que se agrega?
Paso 1: Dejar\(x =\)
Paso 2:
Paso 3:
Paso 4:
Paso 5: El número agregado es __.
- Responder
-
El número agregado es 6.
Conjunto de Muestras B
Dos tercios de un número sumado al recíproco de los rendimientos numéricos\(\dfrac{25}{6}\). ¿Cuál es el número?
Paso 1: Deja\(x = \) el número.
Paso 2: Recordemos que el recíproco de un número\(x\) es el número\(\dfrac{1}{x}\).
\(\dfrac{2}{3} \cdot x + \dfrac{1}{x} = \dfrac{25}{6}\)
\ (\ begin {array} {vaciado a la izquierda}
\ texto {Paso 3:} &\ dfrac {2} {3}\ cdot x +\ dfrac {1} {x} &=\ dfrac {25} {6} &\ text {La LCD es} 6x\ texto {. Multiplica cada término por} 6x\\
& 6x\ cdot\ dfrac {2} {3} x + 6x\ cdot\ dfrac {1} {x} &= 6x\ cdot\ dfrac {25} {6}\\
& 4x^2 + 6 &= 25x &\ text {Resuelve esta ecuación cuadrática no fraccionaria para obtener las soluciones potenciales. (Utilice la propiedad de factor cero.) \\
& 4x^2 - 25x + 6 &= 0\\
& (4x - 1) (x - 6) &= 0\\
& x &=\ dfrac {1} {4}, 6 &\ text {Comprueba estas soluciones potenciales}
\ end {array}\)
Paso 4: Sustituyendo a la ecuación original, puede ser que ambas soluciones verifiquen.
Paso 5: Hay dos soluciones:\(\dfrac{1}{4}\) y\(6\).
Set de práctica B
Siete mitades de un número sumado al recíproco de los rendimientos numéricos\(\dfrac{23}{6}\). ¿Cuál es el número?
Paso 1: Dejar\(x =\)
Paso 2:
Paso 3:
Paso 4:
Paso 5: El número es.
- Responder
-
Hay dos números:\(\dfrac{3}{7}, \dfrac{2}{3}\)
Conjunto de Muestras C
La Persona A, trabajando sola, puede verter una pasarela de concreto en 6 horas. La persona B, trabajando sola, puede verter la misma pasarela en 4 horas. ¿Cuánto tiempo tardarán ambas personas en verter la pasarela de concreto trabajando juntas?
Paso 1: Dejar que\(x = \) el número de horas para verter la pasarela de concreto trabajando en conjunto (ya que esto es lo que estamos buscando).
Paso 2: Si la persona A puede completar el trabajo en 6 horas, A puede completar\(\dfrac{1}{6}\) el trabajo en 1 hora. Si la persona B puede completar el trabajo en 4 horas, B puede completar\(\dfrac{1}{4}\) el trabajo en 1 hora. Si A y B, trabajando juntos, pueden completar el trabajo en\(x\) horas, pueden completar\(\dfrac{1}{x}\) el trabajo en 1 hora. Poniendo estos tres hechos en forma de ecuación, tenemos:
\(\dfrac{1}{6} + \dfrac{1}{4} = \dfrac{1}{x}\)
\ (\ begin {array} {vaciado a la izquierda}
\ text {Paso 3:} &\ dfrac {1} {6} +\ dfrac {1} {4} &=\ dfrac {1} {x} &\ text {Un valor excluido es 0}\\\
& 12x\ cdot\ dfrac {1} {6} +\ dfrac {12x}\ cdot\ frac {1} {4} &= 12x\ cdot\ dfrac {1} {x}\\
& 2x + 3x &= 12 &\ texto { Resuelve esta ecuación no fraccionaria para obtener las soluciones potenciales}\\
& 5x &= 12\\
& x &=\ dfrac {12} {5}\ text {o} x=2\ dfrac {2} {5} &\ text {Comprueba esta solución potencial.}\
\\ text {Paso 4:} &\ dfrac {1} {6} +\ dfrac {1} {4} &=\ dfrac {1} {x}\\
&\ dfrac {1} {6} +\ dfrac {1} {4} =\ dfrac {\ frac {1} {12}} {5}. &\ text {¿Es esto correcto? }\\
&\ dfrac {1} {6} +\ dfrac {1} {4} &=\ dfrac {5} {12} &\ text {La pantalla LCD es} 12\ texto {. ¿Es esto correcto? }\\
&\ dfrac {2} {12} +\ dfrac {3} {12} &=\ dfrac {5} {12} &\ text {¿Es esto correcto? }\\
&\ dfrac {5} {12} &=\ dfrac {5} {12} &\ text {Sí, esto es correcto}
\ end {array}\)
Paso 5: Trabajando juntos, A y B pueden verter la pasarela de concreto en\(2\dfrac{2}{5}\) horas.
Set de práctica C
La Persona A, trabajando sola, puede verter una pasarela de concreto en 9 horas. La persona B, trabajando sola, puede verter la misma pasarela en 6 horas. ¿Cuánto tiempo tardarán ambas personas en verter la pasarela de concreto trabajando juntas?
Paso 1:
Paso 2:
Paso 3:
Paso 4:
Paso 5: Trabajando en conjunto, A y B.
- Responder
-
Trabajando juntos, A y B pueden verter la pasarela de concreto en\(3\dfrac{3}{5}\) hr.
Conjunto de Muestras D
Una tubería de entrada puede llenar un tanque de agua en 12 horas. Una tubería de salida puede drenar el tanque en 20 horas. Si ambas tuberías están abiertas, ¿cuánto tiempo tardará en llenar el tanque?
Paso 1: Dejar x = el número de horas requeridas para llenar el tanque.
Paso 2: Si la tubería de entrada puede llenar el tanque en\(12\) horas, puede llenar\(\dfrac{1}{12}\) el tanque en\(1\) horas.
Si la tubería de salida puede drenar el tanque en 20 horas, puede drenar\(\dfrac{1}{20}\) del tanque en\(1\) horas.
Si ambas tuberías están abiertas, lleva\(x\) horas llenar el tanque. Entonces\(\dfrac{1}{x}\) del tanque se llenará en\(1\) hora.
Dado que se está agregando agua (tubería de entrada) y restando (tubería de salida) obtenemos
\(\dfrac{1}{12} - \dfrac{1}{20} = \dfrac{1}{x}\)
\ (\ begin {array} {vaciado a la izquierda}
\ text {Paso 3:} &\ dfrac {1} {12} -\ dfrac {1} {20} &=\ dfrac {1} {x} &\ text {Un valor excluido es} 0\ text {. La pantalla LCD es} 60x\ text {. Multiplica cada término por} 60x. \\
& 60x\ cdot\ dfrac {1} {12} - 60x\ cdot\ dfrac {1} {20} &= 60x\ cdot\ dfrac {1} {x}\\
& 5x - 3x &= 60 &\ text {Resuelve esta ecuación no fraccionaria para obtener las soluciones potenciales.}\\
& 2x &= 60\
& x &= 30 &\ text { Comprueba esta solución potencial}\\
\ text {Paso 4:} &\ dfrac {1} {12} -\ dfrac {1} {20} &=\ dfrac {1} {x}\\
&\ dfrac {1} {12} -\ dfrac {1} {20} &=\ dfrac {1} {30} &\ text {La LCD es} 60\ texto {. ¿Es esto correcto? }\\
&\ dfrac {5} {60} -\ dfrac {3} {60} &=\ dfrac {1} {30} &\ text {¿Es esto correcto? }\\
&\ dfrac {1} {30} &=\ dfrac {1} {30} &\ text {Sí, esto es correcto}
\ end {array}\)
Paso 5: Con ambas tuberías abiertas, tardará\(30\) horas en llenar el tanque de agua.
Set de Práctica D
Una tubería de entrada puede llenar un tanque de agua en 8 horas y una tubería de salida puede drenar el tanque en 10 horas. Si ambas tuberías están abiertas, ¿cuánto tiempo tardará en llenar el tanque?
Paso 1:
Paso 2:
Paso 3:
Paso 4:
Paso 5:
- Responder
-
Se tardará 40 hr en llenar el tanque.
Juego de Muestras E
La persona A tarda 3 horas más que la persona B en completar un determinado trabajo. Trabajando juntos, ambos pueden completar el trabajo en 2 horas. ¿Cuánto tiempo tarda cada persona en completar el trabajo trabajando sola?
Paso 1: Dejar\(x=\) tiempo requerido para que B complete el trabajo trabajando solo. Entonces,\((x+3) =\) tiempo requerido para que A complete el trabajo trabajando solo.
\ (\ begin {array} {vaciado a la izquierda}
\ texto {Paso 2:} &\ dfrac {1} {x} +\ dfrac {1} {x+3} &=\ dfrac {1} {2}
\\ texto {Paso 3:} &\ dfrac {1} {x} +\ dfrac {1} {x+3} &=\ dfrac {1} {2} &\ text {Los dos valores excluidos son} 0\ text {y} -3\ text {. El LCD es} 2x (x+3)\\
& 2x (x+3)\ cdot\ dfrac {1} {x} + 2x (x+3)\ cdot\ dfrac {1} {x+3} &= 2x (x+3)\ cdot\ dfrac {1} {2}\\
& 2 (x+3) + 2x &= x (x+3)\
& 2x + 6 + 2x &= x^2 + 3x &\ text {Esta es una ecuación cuadrática que se puede resolver usando el método cero- propiedad del factor}\\
& 4x + 6 &= x^2 + 3x\\
& x^2 - x - 6 &= 0\\
& (x-3) (x+2) &= 0\\
& (x-3) (x+2) &= 0\\
& x &= 3, -2 &\ text {Comprobar estas soluciones potenciales}
\ end {array}\)
Paso 4: Si\(x = -2\), la ecuación comprueba, pero ni siquiera tiene sentido físico.
Si\(x = 3\), la ecuación comprueba
\(x = 3\)y\(x + 3 = 6\).
Paso 5: La persona B puede hacer el trabajo en\(3\) horas y la persona A puede hacer el trabajo en\(6\) horas.
Set de práctica E
A la persona A le toma 4 horas menos que a la persona B completar una determinada tarea. Trabajando juntos, ambos pueden completar la tarea en\(\dfrac{8}{3}\) horas. ¿Cuánto tiempo tarda cada persona en completar la tarea trabajando sola?
Paso 1:
Paso 2:
Paso 3:
Paso 4:
Paso 5:
- Responder
-
Persona A, 4 hr para completar la tarea; persona B, 8 hr completar la tarea.
Conjunto de Muestras F
El ancho de un rectángulo es\(\dfrac{1}{3}\) su longitud. Encuentra las dimensiones (largo y ancho) si el permieter es\(16\) cm.
Paso 1: Dejar\(x=\) largo. Después\(\dfrac{x}{3}=\) ancho.
Paso 2: Haz un boceto del rectángulo.
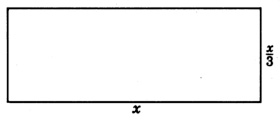
El perímetro de una figura es la longitud total alrededor de la figura.
\ (\ begin {array} {vaciado a la izquierda}
& x +\ dfrac {x} {3} + x +\ dfrac {x} {3} &= 16\\
& 2x +\ dfrac {2x} {3} &= 16
\\ texto {Paso 3:} & 2x +\ dfrac {2x} {3} &= 16 &\ text {La LCD es} 3\
& 3\ cdot 2x + 3\ cdot\ dfrac {2x} {3} &= 3\ cdot 16\\
& 6x + 2x &= 48\\
& 8x &= 48\\
& x &= 6 &\ text {Comprueba esta solución potencial.}\\
\ text {Paso 4:} & 6 +\ dfrac {6} {3} + 6 +\ dfrac {6} {3} &= 16 &\ text {¿Es esto correcto?}
& 6 + 2 + 6 + 2 &= 16 &\ text {¿Es esto correcto?} \\
& 16 &= 16 &\ text {Sí, esto es correcto.}
\ end {array}\)
Desde\(x = 6, \dfrac{x}{3} = \dfrac{6}{3} = 2\)
Paso 5: El largo\(=6\) cm y el ancho\(=2\) cm.
Set de práctica F
El ancho de un rectángulo es\(\dfrac{1}{12}\) su longitud. Encuentra las dimensiones (largo y ancho) si el perímetro es\(78\) pies.
Paso 1:
Paso 2:
Paso 3:
Paso 4:
Paso 5:
- Responder
-
largo = 36 pies, ancho = 3 pies.
Ejercicios
Para los siguientes problemas, resuelva usando el método de cinco pasos.
Cuando se suma el mismo número tanto al numerador como al denominador de la fracción\(\dfrac{3}{7}\), el resultado es\(\dfrac{2}{3}\). ¿Cuál es el número?
- Responder
-
El número agregado es\(5\).
Cuando se suma el mismo número tanto al numerador como al denominador de la fracción\(\dfrac{5}{8}\), el resultado es\(\dfrac{3}{4}\). ¿Cuál es el número?
Cuando se suma el mismo número tanto al numerador como al denominador de la fracción\(\dfrac{3}{8}\), el resultado es\(\dfrac{1}{6}\). ¿Cuál es el número?
- Responder
-
El número agregado es\(−2\).
Cuando se suma el mismo número tanto al numerador como al denominador de la fracción\(\dfrac{7}{9}\), el resultado es\(\dfrac{2}{3}\). ¿Cuál es el número?
Cuando se resta el mismo número tanto al numerador como al denominador de la fracción\(\dfrac{1}{10}\), el resultado es\(\dfrac{2}{3}\). ¿Cuál es el número?
- Responder
-
El número restado es\(−17\).
Cuando se resta el mismo número tanto al numerador como al denominador de la fracción\(\dfrac{3}{4}\), el resultado es\(\dfrac{5}{6}\). ¿Cuál es el número?
Un tercio de un número sumado al recíproco de rendimientos numéricos\(\dfrac{13}{6}\). ¿Cuál es el número?
- Responder
-
\(x= \dfrac{1}{2}, 6\)
Cuatro quintas partes de un número sumado al recíproco de rendimientos numéricos\(\dfrac{81}{10}\). ¿Cuál es el número?
La mitad de un número sumado al doble del recíproco del número rinde\(2\). ¿Cuál es el número?
- Responder
-
\(2\)
Un cuarto de un número sumado a cuatro veces el recíproco de los rendimientos numéricos\(\dfrac{-10}{3}\). ¿Cuál es el número?
Una tubería de entrada puede llenar un tanque en 8 horas. Otra tubería de entrada puede llenar el tanque en 5 horas. ¿Cuánto tiempo tardan ambas tuberías trabajando juntas para llenar el tanque?
- Responder
-
\(3\dfrac{1}{13}\)horas.
Una tubería puede drenar una piscina en 12 horas. Otra tubería puede drenar la piscina en 15 horas. ¿Cuánto tiempo tardan ambas tuberías trabajando juntas para drenar la piscina?
Un grifo puede llenar el lavabo de un baño en 1 minuto. El desagüe puede vaciar el fregadero en 2 minutos. Si tanto el grifo como el desagüe están abiertos, ¿cuánto tiempo tardará en llenar el fregadero?
- Responder
-
dos minutos
Un grifo puede llenar una bañera en\(6\dfrac{1}{2}\) minutos. El desagüe puede vaciar la tina en\(8\dfrac{1}{3}\) minutos. Si tanto el grifo como el desagüe están abiertos, ¿cuánto tiempo tardará en llenar la bañera?
Una tubería de entrada puede llenar un tanque en 5 horas. Una tubería de salida puede vaciar el tanque en 4 horas. Si ambas tuberías están abiertas, ¿se puede llenar el tanque? Explique.
- Responder
-
No. \(x=−20\)horas.
Una tubería de entrada puede llenar un tanque en\(a\) unidades de tiempo. Una tubería de salida puede vaciar el tanque en\(b\) unidades de tiempo. Si ambas tuberías están abiertas, ¿cuántas unidades de tiempo se requieren para llenar el tanque? ¿Hay alguna restricción sobre\(a\) y\(b\)?
Un repartidor, trabajando solo, puede entregar todos sus bienes en 6 horas. Otro repartidor, que trabaja solo, puede entregar la misma mercancía en 5 horas. ¿Cuánto tiempo tardarán los chicos en entregar todos los bienes trabajando juntos?
- Responder
-
\(2\dfrac{8}{11}\)horas.
Un astronauta del transbordador espacial puede realizar cierto experimento en 2 horas. Otro astronauta del transbordador espacial que no esté tan familiarizado con el experimento puede realizarlo en\(2\dfrac{1}{2}\) horas. Trabajando juntos, ¿cuánto tardarán ambos astronautas en realizar el experimento?
Una persona puede completar una tarea 8 horas antes que otra persona. Trabajando en conjunto, ambas personas pueden realizar la tarea en 3 horas. ¿Cuántas horas le toma a cada persona completar la tarea trabajando sola?
- Responder
-
Primera persona: 12 horas; segunda persona: 4 horas
Encuentra dos enteros consecutivos de tal manera que dos tercios del número menor agregado al otro rinda 11.
Encuentra dos enteros consecutivos de tal manera que tres cuartas partes del número menor sumado al otro rinde 29.
- Responder
-
16,17
El ancho de un rectángulo es\(\dfrac{2}{5}\) su longitud. Encuentra las dimensiones si el perímetro es de 42 metros.
El ancho de un rectángulo es\(\dfrac{3}{7}\) el largo. Encuentra las dimensiones si el perímetro es de 60 pies.
- Responder
-
ancho=9 ft; largo=21 ft
Dos lados de un triángulo tienen la misma longitud. El tercer lado es el doble de largo que cualquiera de los otros dos lados. El perímetro del triángulo es de 56 pulgadas. ¿Cuál es la longitud de cada lado?
En un triángulo, el segundo lado es 3 pulgadas más largo que el primer lado. El tercer lado es\(\dfrac{3}{4}\) la longitud del segundo lado. Si el perímetro es de 30 pulgadas, ¿cuánto dura cada lado?
- Responder
-
lado 1=9 pulgadas; lado 2=12 pulgadas; lado 3=9 pulgadas
la presión debida a la tensión superficial en una caída esférica de líquido viene dada por\(P=\dfrac{2T}{r}\), donde\(T\) está la tensión superficial del líquido y\(r\) es el radio de la gota. Si el líquido es una burbuja, tiene dos superficies y la tensión superficial viene dada por
\(P = \dfrac{2T}{r} + \dfrac{2T}{r} = \dfrac{4T}{r}\)
(a) Determinar la presión debida a la tensión superficial dentro de una burbuja de jabón de radio de 2 pulgadas y tensión superficial 28.
(b) Determinar el radio de una burbuja si la presión debida a la tensión superficial es 52 y la tensión superficial es 39.
La ecuación\(\dfrac{1}{p} + \dfrac{1}{q} = \dfrac{1}{f}\) relaciona la distancia\(p\) de un objeto desde una lente y la distancia\(q\) de imagen desde la lente con la distancia focal\(f\) de la lente.
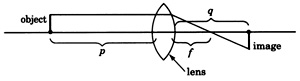
(a) Determinar la distancia focal de una lente en la que un objeto a 10 pies de distancia produce una imagen a 6 pies de distancia.
(b) Determinar qué tan lejos está un objeto de una lente si la distancia focal de la lente es de 6 pulgadas y la distancia de la imagen es de 10 pulgadas.
(c) Determinar qué tan lejos estará una imagen de una lente que tenga una distancia focal de\(4\dfrac{4}{5}\) cm y el objeto esté a 12 cm de distancia de la lente.
- Responder
-
a)\(f = \dfrac{15}{4}\) pies
b)\(p = 15\) pulgadas.
c)\(q = 8\) cm.
La persona A puede completar una tarea en 4 horas, la persona B puede completar la tarea en 6 horas y la persona C puede completar la tarea en 3 horas. Si las tres personas están trabajando juntas, ¿cuánto tiempo tardará en completar la tarea?
Tres tuberías de entrada pueden llenar un tanque de almacenamiento en 4, 6 y 8 horas, respectivamente. ¿Cuánto tiempo tardarán las tres tuberías en llenar el tanque?
- Responder
-
\(1\dfrac{11}{13}\)horas
Una tubería de entrada puede llenar un tanque en 10 horas. El tanque tiene dos tuberías de drenaje, cada una de las cuales puede vaciar el tanque en 30 horas. Si las tres tuberías están abiertas, ¿se puede llenar el tanque? Si es así, ¿cuánto tiempo tardará?
Una tubería de entrada puede llenar un tanque en 4 horas. El tanque tiene tres tubos de drenaje. Dos de las tuberías de drenaje pueden vaciar el tanque en 12 horas, y la tercera puede vaciar el tanque en 20 horas. Si las cuatro tuberías están abiertas, ¿se puede llenar el tanque? Si es así, ¿cuánto tiempo tardará?
- Responder
-
30 horas
Ejercicios para revisión
Factor\(12a^2 + 13a - 4\).
Encuentra la pendiente de la línea que pasa por los puntos\((4, -3)\) y\((1, -6)\).
- Responder
-
\(m=1\)
Encuentra el cociente:\(\dfrac{2 x^{2}-11 x-6}{x^{2}-2 x-24} \div \dfrac{2 x^{2}-3 x-2}{x^{2}+2 x-8}\)
Encuentra la diferencia:\(\dfrac{x+2}{x^{2}+5 x+6}-\dfrac{x+1}{x^{2}+4 x+3}\)
- Responder
-
\(0\)
Resolver la ecuación\(\dfrac{9}{2m-5} = -2\)