16.3: La línea numérica real y los números reales

Última actualización
Guardar como PDF

Page ID: 161859

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

La línea del número real

Línea de número real

En nuestro estudio del álgebra, utilizaremos varias colecciones de números. La línea numérica real nos permite mostrar visualmente los números en los que estamos interesados.

Una línea está compuesta por infinitamente muchos puntos. A cada punto podemos asociar un número único, y con cada número podemos asociar un punto en particular.

Coordinar

El número asociado a un punto en la recta numérica se denomina coordenada del punto.

Gráfica

El punto en una línea que está asociado a un número determinado se llama la gráfica de ese número.

Construimos la línea numérica real de la siguiente manera:

Construcción de la Línea de Número Real

1. Dibuja una línea horizontal.

$clipboard_ebf011d33286921b055318f1175a31691.png$

2. Elija cualquier punto de la línea y etiquételo 0. A este punto se le llama el origen.

$clipboard_e35db316e7c133494c6c6e133afa6a0c3.png$

3. Elija una longitud conveniente. Esta longitud se llama “1 unidad”. A partir de 0, marca esta longitud en ambas direcciones, teniendo cuidado de que las longitudes parezcan que son aproximadamente las mismas.

$clipboard_ee10cdc061196e7df1dcfd5d8978ba5b8.png$

Número Real

Un número real es cualquier número que es la coordenada de un punto en la línea numérica real.

Números reales positivos y negativos

A la colección de estos infinitamente muchos números se le llama colección de números reales. Los números reales cuyas gráficas están a la derecha de 0 se denominan números reales positivos. Los números reales cuyas gráficas aparecen a la izquierda de 0 se denominan números reales negativos.

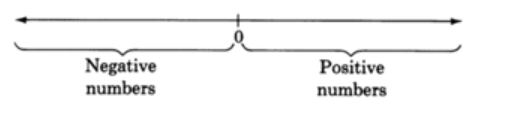
$clipboard_eb2addbfdffe7c49ded5956d8faec2199.png$

El número 0 no es ni positivo ni negativo.

Los números reales

La colección de números reales tiene muchas subcolecciones. A continuación se enumeran las subcolecciones que más nos interesan junto con sus anotaciones y gráficas.

Números naturales:

Los números naturales ($N$):${1, 2, 3, ...}$

$clipboard_efddaa9170192b3568cefe96384fb4569.png$

Números Enteros:

Los números enteros ($W$):${0, 1, 2, 3, ...}$

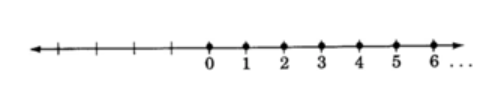
$clipboard_e172eb8501d7fb928ca3576b15293c3ae.png$

Observe que cada número natural es un número entero.

Enteros:

Los enteros ($Z$):${..., -3, -2, -1, 0, 1, 2, 3, ...}$

$clipboard_e44cf4b66efe6bbd078a7666fc8e99bee.png$

Observe que cada número entero es un entero.

Números racionales

Los números racionales (Q): Los números racionales son números reales que se pueden escribir en la forma$\dfrac{a}{b}$, donde$a$ y$b$ son enteros, y$b \not= 0$.

Fracciones

Los números racionales se llaman comúnmente fracciones.

División por 1

Dado que$b$ puede ser igual a 1, cada entero es un número racional:$\dfrac{a}{1} = a$.

División por 0

Recordemos que$\dfrac{10}{2} = 5$ desde$2 \cdot 5 = 10$. Sin embargo, si$\dfrac{10}{0} = x$, entonces$0 \cdot x = 10$. Pero$0 \cdot x = 0$, no 10. Esto sugiere que no existe cociente.

Ahora considere$\dfrac{0}{0} = x$. Si$\dfrac{0}{0} = x$, entonces$0 \cdot x = 0$. Pero esto quiere decir que$x$ podría ser cualquier número, es decir$\dfrac{0}{0} = 4$ desde$0 \cdot 4 = 0$, o$\dfrac{0}{0} = 28$ desde entonces$0 \cdot 28 = 0$. Esto sugiere que el cociente es indeterminante.

$\dfrac{x}{0}$ is Undefined or Indeterminant

La división por 0 es indefinida o indeterminante.

No dividir por 0.

Los números racionales tienen representaciones decimales que terminan o no terminan pero contienen un bloque repetido de dígitos. Algunos ejemplos son:

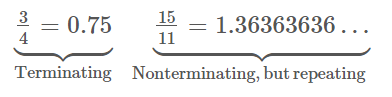
$clipboard_e6f6fc9732d1b811fb9d184583aa766d1.png$

Algunos números racionales se graficaron a continuación.

$clipboard_e094615f9e89b6adc8bb5f76463ad5b26.png$

Números irracionales

Los números irracionales (Ir): Los números irracionales son números que no pueden escribirse como cociente de dos enteros. Son números cuyas representaciones decimales son no terminadoras y no repetitivas. Algunos ejemplos son

$4.01001000100001... \pi = 3.1415927...$

Observe que las colecciones de números racionales y números irracionales no tienen números en común.

Cuando se grafica en la recta numérica, los números racionales e irracionales dan cuenta de cada punto en la recta numérica. Así, cada punto de la recta numérica tiene una coordenada que es un número racional o irracional.

En resumen, tenemos

Conjunto de Muestras A

El cuadro de resumen ilustra que

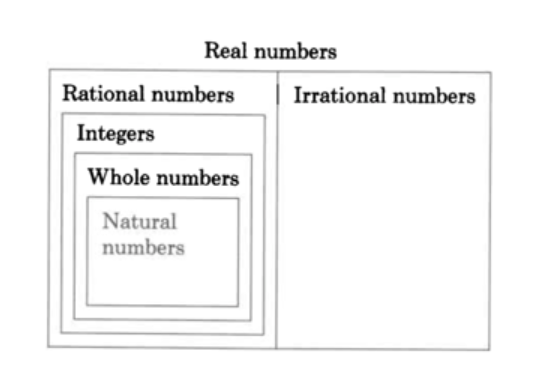
$clipboard_e89cc71e5ed2ede539c163fc1194608a3.png$

- Cada número natural es un número real

- Cada número entero es un número real.

- Ningún entero es un número irracional.

Conjunto de práctica A

Problema de práctica$\PageIndex{1}$

¿Cada número natural es un número entero?

Contestar: Sí

Problema de práctica$\PageIndex{2}$

¿Cada número entero es un número entero?

Contestar: Sí

Problema de práctica$\PageIndex{3}$

¿Cada entero es un número racional?

Contestar: Sí

Problema de práctica$\PageIndex{4}$

¿Cada número racional es un número real?

Contestar: Sí

Problema de práctica$\PageIndex{5}$

¿Cada entero es un número natural?

Contestar: No

Problema de práctica$\PageIndex{6}$

¿Hay un número entero que sea un número natural?

Contestar: Sí

Ordenar los números reales

Ordenar los números reales

Se dice que un número real$b$ es mayor que un número real$a$, denotado$b > a$, si la gráfica de$b$ está a la derecha de la gráfica de$a$ en la recta numérica.

Conjunto de Muestras B

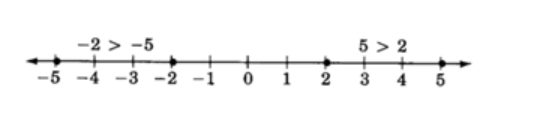
Como es de esperar,$5 > 2$ ya que$5$ está a la derecha de$2$ en la recta numérica. También,$−2 > −5$ ya que$−2$ está a la derecha de$−5$ en la recta numérica.

$clipboard_efd700fd481fa0e6e2595618c45968e12.png$

Set de práctica B

Problema de práctica$\PageIndex{7}$

¿Todos los números positivos son mayores a 0?

Contestar: Sí

Problema de práctica$\PageIndex{8}$

¿Todos los números positivos son mayores que todos los números negativos?

Contestar: Sí

Problema de práctica$\PageIndex{9}$

¿Es 0 mayor que todos los números negativos?

Contestar: Sí

Problema de práctica$\PageIndex{10}$

¿Hay un mayor número positivo? ¿Hay un número negativo más pequeño?

Contestar: No, No.

Problema de práctica$\PageIndex{11}$

¿Cuántos números reales hay? ¿Cuántos números reales hay entre 0 y 1?

Contestar: infinitamente muchos, infinitamente muchos

Conjunto de Muestras C

Ejemplo$\PageIndex{1}$

¿Qué enteros pueden reemplazar$x$ para que la siguiente afirmación sea verdadera?

\[ -4 \le x < 2 \]

Esta afirmación indica que el número representado por$x$ es entre$-4$ y$2$. Específicamente,$-4$ es menor o igual a$x$, y al mismo tiempo,$x$ es estrictamente menor que$2$. Esta afirmación es un ejemplo de una desigualdad compuesta.

$clipboard_eb31f5747ea1ce3aed62a2fc3c287165a.png$

Los enteros son$-4, -3, -2, -1, 0, 1$.

Ejemplo$\PageIndex{2}$

Dibuja una recta numérica que se extienda de −3 a 7. Coloque puntos en todos los números enteros entre e incluyendo −2 y 6.

Ejemplo$\PageIndex{3}$

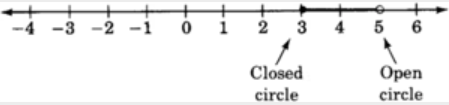
Dibuja una línea numérica que se extienda desde$−4$$6$ y coloque puntos en todos los números reales mayores o iguales$3$ pero estrictamente menores que$5$.

$clipboard_ec53f98910eb255a2a5c9c1d8d6e5cfce.png$

Se acostumbra usar un círculo cerrado para indicar que un punto está incluido en la gráfica y un círculo abierto para indicar que un punto no está incluido.
$clipboard_ead6f8119707a3b3645242837cb272ec0.png$

Set de práctica C

Problema de práctica$\PageIndex{12}$

¿Qué números enteros pueden reemplazar x para que la siguiente afirmación sea verdadera?

$-3 \le x < 3$

Contestar: 0, 1, 2

Problema de práctica$\PageIndex{12}$

Dibuja una línea numérica que se extienda de −5 a 3 y coloque puntos en todos los números mayores o iguales a −4 pero estrictamente menores que 2.

$clipboard_eb4300c65a652f7ffbb091bca1197d17a.png$

Contestar: $clipboard_ec4451059287d12ec85c5a93a530b63f5.png$

Ejercicios

Para los siguientes problemas, junto a cada número real, anote todas las colecciones a las que pertenece escribiendo$N$ para números naturales,$W$ para números enteros,$Z$ para números enteros,$Q$ para números racionales,$Ir$ para números irracionales y$R$ para números reales. Algunos números pueden requerir más de una letra.

Ejercicio$\PageIndex{1}$

$\dfrac{1}{2}$

Contestar: $Q, R$

Ejercicio$\PageIndex{2}$

$-12$

Ejercicio$\PageIndex{3}$

Contestar: $W, Z, Q, R$

Ejercicio$\PageIndex{4}$

$-24\dfrac{7}{8}$

Ejercicio$\PageIndex{5}$

$86.3333...$

Contestar: $Q, R$

Ejercicio$\PageIndex{6}$

$49.125125125...$

Ejercicio$\PageIndex{7}$

$-15.07$

Contestar: $Q, R$

Para los siguientes problemas, dibuje una recta numérica que se extienda desde$−3$ hasta$3$. Localice cada número real en la recta numérica colocando un punto (círculo cerrado) en su ubicación aproximada.

Ejercicio$\PageIndex{8}$

$1 \dfrac{1}{2}$

Ejercicio$\PageIndex{9}$

$ -2$

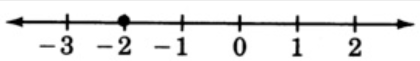
Contestar: $clipboard_e07ba9bf9cc0e80e33907f99fac5f81d4.png$

Ejercicio$\PageIndex{10}$

$ - \dfrac{1}{8}$

Ejercicio$\PageIndex{11}$

¿0 es un número positivo, negativo, ninguno, o ambos?

Contestar: ni

Ejercicio$\PageIndex{12}$

Un entero es un número entero par si se puede dividir por 2 sin un resto; de lo contrario, el número es impar. Dibuja una línea numérica que se extienda de −5 a 5 y coloque puntos en todos los enteros pares negativos y en todos los enteros impares positivos.

Ejercicio$\PageIndex{13}$

Dibuja una recta numérica que se extienda de −5 a 5. Coloque los puntos en todos los enteros estrictamente mayores que −3 pero estrictamente menores que 4.

Contestar: $clipboard_e0ad1dfd74e22ebe0e4cbd12d09dd9d68.png$

Para los siguientes problemas, dibuje una recta numérica que se extienda de −5 a 5. Colocar puntos en todos los números reales entre e incluyendo cada par de números

Ejercicio$\PageIndex{14}$

$-5$y$-2$

Ejercicio$\PageIndex{15}$

$-3$y$4$

Contestar: $clipboard_e337288b94951fd34b0aa27230b66568f.png$

Ejercicio$\PageIndex{16}$

−4 y 0

Ejercicio$\PageIndex{17}$

Dibuja una recta numérica que se extienda de −5 a 5. ¿Es posible localizar algún número que sea estrictamente mayor que 3 pero también estrictamente menor que −2?

Contestar

$clipboard_e784fdfe903e5fbbaaa8dbb882dcbe209.png$

Para los pares de números reales mostrados en los siguientes problemas, escriba el símbolo de relación apropiado (<, >, =) en lugar de la ∗.

Ejercicio$\PageIndex{18}$

−5×−1

Ejercicio$\PageIndex{19}$

−3×0

Contestar: <

Ejercicio$\PageIndex{20}$

−4×7

Ejercicio$\PageIndex{21}$

6×−1

Contestar: >

Ejercicio$\PageIndex{22}$

$\dfrac{1}{4}$*$-\dfrac{3}{4}$

Ejercicio$\PageIndex{23}$

¿Hay un número real más grande? Si es así, ¿qué es?

Contestar: no

Ejercicio$\PageIndex{24}$

¿Hay un entero más grande? Si es así, ¿qué es?

Ejercicio$\PageIndex{25}$

¿Hay un número entero de dos dígitos más grande? Si es así, ¿qué es?

Contestar: 99

Ejercicio$\PageIndex{26}$

¿Hay un entero más pequeño? Si es así, ¿qué es?

Ejercicio$\PageIndex{27}$

¿Hay un número entero más pequeño? Si es así, ¿qué es?

Contestar: si, 0

Para los siguientes problemas, ¿qué números pueden sustituir$x$ para que las siguientes afirmaciones sean ciertas?

Ejercicio$\PageIndex{28}$

$-1 \le x \le 5$,$x$ un entero

Ejercicio$\PageIndex{29}$

$ -7 < x < -1$,$x$ un entero

Contestar: $-6, -5, -4, -3, -2$

Ejercicio$\PageIndex{30}$

$-3 \le x \le 2$,$x$ un número natural

Ejercicio$\PageIndex{31}$

$-15 < x \le -1$,$x$ un número natural

Contestar: No hay números naturales entre$-15$ y$-1$.

Ejercicio$\PageIndex{32}$

$-5 \le x < 5$,$x$ un número entero

Ejercicio$\PageIndex{33}$

La temperatura en el desierto hoy era de noventa y cinco grados. Representar esta temperatura por un número racional.

Contestar: $\dfrac{95}{1}$

Ejercicio$\PageIndex{34}$

La temperatura hoy en Colorado Springs era de ocho grados bajo cero. Representar esta temperatura con un número real.

Ejercicio$\PageIndex{35}$

¿Cada entero es un número racional?

Contestar: Sí

Ejercicio$\PageIndex{36}$

¿Cada número racional es un número entero?

Ejercicio$\PageIndex{37}$

¿Se pueden sumar dos números racionales para producir un número entero? Si es así, dar un ejemplo.

Contestar: Sí. $\dfrac{1}{2} + \dfrac{1}{2} = 1$o$1 + 1 = 2$

Para los siguientes problemas, en la recta numérica, ¿cuántas unidades (intervalos) hay entre ellas?

Ejercicio$\PageIndex{38}$

0 y 2

Ejercicio$\PageIndex{39}$

-5 y 0

Contestar: 5 unidades

Ejercicio$\PageIndex{40}$

0 y 6

Ejercicio$\PageIndex{41}$

-8 y 0

Contestar: 8 Unidades

Ejercicio$\PageIndex{42}$

-3 y 4

Ejercicio$\PageIndex{43}$

$m$y$n$,$m > n$

Contestar: $m - n$unidades

Ejercicio$\PageIndex{44}$

$-a$y$-b$,$-b > -a$

Ejercicios para la revisión

Ejercicio$\PageIndex{45}$

Encuentra el valor de$6 + 3(15 - 8) - 4$

Contestar: 23

Ejercicio$\PageIndex{46}$

Encuentra el valor de$5(8 - 6) + 3(5 + 2 \cdot 3$

Ejercicio$\PageIndex{47}$

¿Son las declaraciones$y < 4$ y$y \ge 4$ las mismas o diferentes?

Contestar: Diferente

Ejercicio$\PageIndex{48}$

Utilice la notación algebraica para escribir la sentencia “seis veces un número es menor o igual a once”.

Ejercicio$\PageIndex{49}$

¿La afirmación es$8(15 - 3 \cdot 4) - 3 \cdot 7 \ge 3$ verdadera o falsa?

Contestar: true

Search

Text Color

Text Size

Margin Size

Font Type

Coordinar

Gráfica

Construcción de la Línea de Número Real

Número Real

Números racionales

Fracciones

División por 1

División por 0

\(\dfrac{x}{0}\) is Undefined or Indeterminant

Números irracionales

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)