16.5: Exponentes
- Page ID
- 161861
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Visión general
- Notación exponencial
- Lectura de Notación Exponencial
- El orden de operaciones
Notación exponencial
En la Sección 2.4 se nos recordó que la multiplicación es una descripción para la adición repetida. Una pregunta natural es “¿Existe una descripción para la multiplicación repetida?” La respuesta es sí. La notación que describe la multiplicación repetida es la notación exponencial.
Factores
En la multiplicación, los números que se multiplican entre sí se denominan factores. En multiplicación repetida, todos los factores son iguales. En la multiplicación no repetida, ninguno de los factores es el mismo. Por ejemplo,
\(18 \cdot 18 \cdot 18 \cdot 18\)Multiplicación repetida de 18. Los cuatro factores, 18 son iguales.
\(x \cdot x \cdot x \cdot x \cdot x\)Multiplicación repetida de\(x\). Los cinco factores\(x\),, son iguales.
\(3 \cdot 7 \cdot a\)Multiplicación no repetida. Ninguno de los factores es el mismo.
La notación exponencial se utiliza para mostrar multiplicación repetida del mismo factor. La notación consiste en utilizar un superíndice sobre el factor que se repite. Al superíndice se le llama exponente.
Notación exponencial Si\(x\) es cualquier número real y\(n\) es un número natural, entonces
\(x^{n}=\underbrace{x \cdot x \cdot x \cdot \ldots \cdot x}_{n \text { factors of } x}\)
Un exponente registra el número de factores idénticos en la multiplicación.
Tenga en cuenta que la definición de notación exponencial solo tiene significado para exponentes numéricos naturales. Ampliaremos esta notación para incluir otros números como exponentes posteriormente.
Conjunto de Muestras A
\(7 \cdot 7 \cdot 7 \cdot 7 \cdot 7 \cdot 7 = 7^6\)
El factor repetido es 7. El exponente 6 registra el hecho de que 7 aparece 6 veces en la multiplicación.
\(x \cdot x \cdot x \cdot x = x^4\)
El factor repetido es\(x\). El exponente 4 registra el hecho que\(x\) aparece 4 veces en la multiplicación.
\((2y)(2y)(2y) = (2y)^3\)
El factor repetido es\(2y\). El exponente 3 registra el hecho de que el factor\(2y\) aparece 3 veces en la multiplicación.
\(2yyy = 2y^3\)
El factor repetido es\(y\). El exponente 3 registra el hecho de que el factor\(y\) aparece 3 veces en la multiplicación.
\((a + b)(a + b)(a - b)(a - b)(a - b) = (a + b)^2(a - b)^3\)
Los factores repetidos son\((a + b)\) y\((a - b)\),\((a + b)\) apareciendo 2 veces y\((a - b)\) apareciendo 3 veces.
Conjunto de práctica A
Escribe cada uno de los siguientes usando exponentes.
Problema de práctica\(\PageIndex{1}\)
\(a \cdot a \cdot a \cdot a\)
- Contestar
-
\(a^4\)
Problema de práctica\(\PageIndex{2}\)
\((3b)(3b)(5c)(5c)(5c)(5c)\)
- Contestar
-
\((3b)^2(5c)^4\)
Problema de práctica\(\PageIndex{3}\)
\(2 \cdot 2 \cdot 7 \cdot 7 \cdot 7 \cdot (a - 4)(a - 4)\)
- Contestar
-
\(2^2 \cdot 7^3(a - 4)^2\)
Problema de práctica\(\PageIndex{4}\)
\(8xxxyzzzzz\)
- Contestar
-
\(8x^3yz^5\)
Conjunto de Muestras B
\(8x^3\)significa\(8 \cdot xxx\) y no\(8x8x8x\). El exponente\(3\) aplica sólo al factor\(x\) ya que es sólo al factor\(x\) que el\(3\) está conectado.
\((8x)^3\)significa\((8x)(8x)(8x)\) ya que los paréntesis indican que el exponente\(3\) está directamente conectado al factor\(8x\). Recuerde que los símbolos de agrupación () indican que las cantidades en su interior deben considerarse como un solo número.
\(34(a+1)^2\)significa\(34 \cdot (a+1)(a+1)\) ya que el exponente\(2\) se aplica únicamente al factor\((a+1)\).
Set de práctica B
Escribe cada uno de los siguientes sin exponentes.
Problema de práctica\(\PageIndex{5}\)
\(4a^3\)
- Contestar
-
\(4aaa\)
Problema de práctica\(\PageIndex{6}\)
\((4a)^3\)
- Contestar
-
\((4a)(4a)(4a)\)
Conjunto de Muestras C
Seleccione un número para mostrar que\((2 x)^{2}\) no siempre sea igual a\(2 x^{2}\).
Supongamos\(x\) que elegimos ser 5. Considere ambos\((2 x)^{2}\) y\(2 x^{2}\).
\ (
\ begin {array} {ll}
(2 x) ^ {2} & 2 x^ {2}\\
(2\ cdot 5) ^ {2} & 2\ cdot 5^ {2}\
(10) ^ {2} & 2\ cdot 25\\
100 &\ neq 50
\ end {array}
\)
Observe que \((2 x)^{2}=2 x^{2}\)sólo cuando\(x=0\).
Set de práctica C
Problema de práctica\(\PageIndex{7}\)
Seleccione un número para mostrar que\((5x)^2\) no siempre sea igual a\(5x^2\)
- Responder
-
Seleccione\(x=3\). Entonces\((5 \cdot 3)^2 = (15)^2 = 225\), pero\(5 \cdot 3^2 = 5 \cdot 9 = 45\). \(225 \not = 45\)
Lectura de Notación Exponencial
\(ln(x^n)\)
Base
\(x\) es la base.
El exponente
\(n\) es el exponente.
Poder
El número representado por\(x^n\) se llama poder.
\(x\)al\(n\) th Poder
El término\(x^n\) se lee como "\(x\)al\(n\) th poder”, o más simplemente como "\(x\)al\(n\) th.”
\(x\)Cuadrados y\(x\) Cubicados
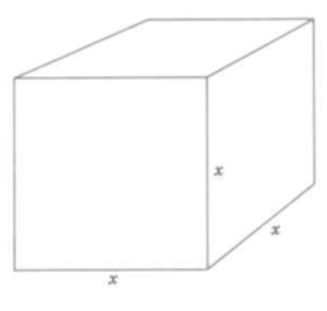
El símbolo a menudo\(x^2\) se lee como "\(x\)cuadrado”, y a menudo\(x^3\) se lee como "en\(x\) cubos”. Una pregunta natural es “¿Por qué aparecen términos geométricos en la expresión exponente?” La respuesta para\(x^3\) es esta:\(x^3\) medios\(x \cdot x \cdot x\). En geometría, el volumen de una caja rectangular se encuentra multiplicando el largo por el ancho por la profundidad. Un cubo tiene la misma longitud en cada lado. Si representamos esta longitud por la letra\(x\) entonces el volumen del cubo es\(x \cdot x \cdot x\), que, por supuesto, es descrito por\(x^3\). (¿Se te ocurre por qué\(x^2\) se lee como\(x\) cuadrado?)
Cubo con
largo =\(x\)
ancho =\(x\)
profundidad =\(x\)
Volumen =\(xxx\) =\(x^3\)
El orden de operaciones
En la Sección 4.2 nos presentaron el orden de operaciones. Se señaló que insertaríamos otra operación antes de la multiplicación y división. Ya podemos hacer eso.
- Realice todas las operaciones dentro de los símbolos de agrupación comenzando con el conjunto más interno.
- Realiza todas las operaciones exponenciales a medida que llegas a ellas, moviéndote de izquierda a derecha.
- Realiza todas las multiplicaciones y divisiones a medida que llegas a ellas, moviéndote de izquierda a derecha.
- Realiza todas las adiciones y restas a medida que llegas a ellas, moviéndote de izquierda a derecha.
Conjunto de Muestras D
Utilice el orden de las operaciones para simplificar cada una de las siguientes.
\(2^2 + 5 = 4 + 5 = 9\)
\(5^2 + 3^2 + 10 = 25 + 9 + 10 = 44\)
\ (
\ begin {alineado}
2^ {2} + (5) (8) -1 &=4+ (5) (8) -1\\
&=4+40-1\\
&=43
\ end {alineado}
\)
\ (
\ begin {alineado}
7\ cdot 6-4^ {2} +1^ {5} &=7\ cdot 6-16+1\\
&=42-16+1\\
&=27
\ end {alineado}
\)
\ (
\ begin {alineado}
(2+3) ^ {3} +7^ {2} -3 (4+1) ^ {2} & =( 5) ^ {3} +7^ {2} -3 (5) ^ {2}\
&=125+49-3 (25)\\
&=125+49-75
\ end {alineado}
\)
\ (
\ begin {alineado}
\ izquierda [4 (6+2) ^ {3}\ derecha] ^ {2} &=\ izquierda [4 (8) ^ {3}\ derecha] ^ {2}\\
&= [4 (512)] ^ {2}\\
&= [2048] ^ {2}\\
&=4.194.304
\ end {alineado}
\)
\ (
\ begin {alineado}
6\ izquierda (3^ {2} +2^ {2}\ derecha) +4^ {2} &=6 (9+4) +4^ {2}\\
&=6 (13) +4^ {2}\\
&=6 (13) +16\\
&=78+16\\
&=94
\ end {alineado}
\)
\ (
\ begin {alineado}
\ dfrac {6^ {2} +2^ {2}} {4^ {2} +6\ cdot 2^ {2}} +\ dfrac {1^ {3} +8^ {2}} {10^ {2} - (19) (5)} &=\ dfrac {36+4} {16+6\ cdot 4} +\ dfrac {1+64} {100-95}\
&=\ dfrac {36+4} {16+24} +\ dfrac {1+64} {100-95}\\
&=\ dfrac {40} {40} +\ dfrac {65} {5}\\
&=1+13\\
&=14
\ end {alineado}
\)
Set de Práctica D
Utilice el orden de operaciones para simplificar lo siguiente.
Problema de práctica\(\PageIndex{8}\)
\(3^2 + 4 \cdot 5\)
- Responder
-
29
Problema de práctica\(\PageIndex{9}\)
\(2^3 + 3^3 - 8 \cdot 4\)
- Responder
-
3
Problema de práctica\(\PageIndex{10}\)
\(1^4 + (2^2 + 4)^2 \div 2^3\)
- Responder
-
9
Problema de práctica\(\PageIndex{11}\)
\([6(10 - 2^3)]^2 - 10^2 - 6^2\)
- Responder
-
8
Problema de práctica\(\PageIndex{12}\)
\(\dfrac{5^2 + 6^2 - 10}{1 + 4^2} + \dfrac{0^4 - 0^5}{7^2 - 6 \cdot 2^3}\)
- Responder
-
3
Ejercicios
Para los siguientes problemas, escriba cada una de las cantidades usando notación exponencial.
Ejercicio\(\PageIndex{1}\)
\(b\)al cuarto
- Responder
-
\(b^4\)
Ejercicio\(\PageIndex{2}\)
\(a\)al cuadrado
Ejercicio\(\PageIndex{3}\)
\(x\)a la octava
- Responder
-
\(x^8\)
Ejercicio\(\PageIndex{4}\)
\((-3)\)en cubos
Ejercicio\(\PageIndex{5}\)
\(5\)tiempos\(s\) al cuadrado
- Responder
-
\(5s^2\)
Ejercicio\(\PageIndex{6}\)
\(3\)tiempos cuadrados\(y\) a la quinta
Ejercicio\(\PageIndex{7}\)
\(a\)cubicado menos\((b + 7)\) cuadrado
- Responder
-
\(a^3 - (b + 7)^2\)
Ejercicio\(\PageIndex{8}\)
\((21 - x)\)cubos más\(x + 5\) al séptimo
Ejercicio\(\PageIndex{9}\)
\(xxxxx\)
- Responder
-
\(x^5\)
Ejercicio\(\PageIndex{10}\)
\((8)(8)xxxx\)
Ejercicio\(\PageIndex{11}\)
\(2 \cdot 3 \cdot 3 \cdot 3 \cdot 3xxyyyyy\)
- Responder
-
\(2(3^4)x^2y^5\)
Ejercicio\(\PageIndex{12}\)
\(2 \cdot 2 \cdot 5 \cdot 6 \cdot 6 \cdot 6xyyzzzwwww\)
Ejercicio\(\PageIndex{13}\)
\(7xx(a + 8)(a + 8)\)
- Responder
-
\(7x^2(a + 8)^2\)
Ejercicio\(\PageIndex{14}\)
\(10xyy(c + 5)(c + 5)(c + 5)\)
Ejercicio\(\PageIndex{15}\)
\(4x4x4x4x4x\)
- Responder
-
\((4x)^5\)o\(4^5x^5\)
Ejercicio\(\PageIndex{16}\)
\((9a)(9a)(9a)(9a)\)
Ejercicio\(\PageIndex{17}\)
\((-7)(-7)(-7)aabbba(-7)baab\)
- Responder
-
\((-7)^4a^5b^5\)
Ejercicio\(\PageIndex{18}\)
\((a - 10)(a - 10)(a + 10)\)
Ejercicio\(\PageIndex{19}\)
\((z + w)(z + w)(z + w)(z - w)(z - w)\)
- Responder
-
\((z + w)^3(z - w)^2\)
Ejercicio\(\PageIndex{20}\)
\((2y)(2y)2y2y\)
Ejercicio\(\PageIndex{21}\)
\(3xyxxy - (x + 1)(x + 1)(x + 1)\)
- Responder
-
\(3x^3y^2 - (x + 1)^3\)
Para los siguientes problemas, ampliar las cantidades para que no aparezcan exponentes.
Ejercicio\(\PageIndex{22}\)
\(4^3\)
Ejercicio\(\PageIndex{23}\)
\(6^2\)
- Responder
-
\(6 \cdot 6\)
Ejercicio\(\PageIndex{24}\)
\(7^3y^2\)
Ejercicio\(\PageIndex{25}\)
\(8x^3y^2\)
- Responder
-
\(8 \cdot x \cdot x \cdot x \cdot y \cdot y\)
Ejercicio\(\PageIndex{26}\)
\((18x^2y^4)^2\)
Ejercicio\(\PageIndex{27}\)
\((9a^3b^2)^3\)
- Responder
-
\((9aaabb)(9aaabb)(9aaabb)\)o\(9 \cdot 9 \cdot 9aaaaaaaaabbbbbb\)
Ejercicio\(\PageIndex{28}\)
\(5x^2(2y^3)^3\)
Ejercicio\(\PageIndex{29}\)
\(10a^3b^2(3c)^2\)
- Responder
-
\(10aaabb(3c)(3c)\)o\(10 \cdot 3 \cdot 3aaabbcc\)
Ejercicio\(\PageIndex{30}\)
\((a + 10)^2(a^2 + 10)^2\)
Ejercicio\(\PageIndex{31}\)
\((x^2 - y^2)(x^2 + y^2)\)
- Responder
-
\((xx - yy)(xx + yy)\)
Para los siguientes problemas, seleccione un número (o números) para mostrar que
Ejercicio\(\PageIndex{32}\)
\((5x)^2\)generalmente no es igual a\(5x^2\).
Ejercicio\(\PageIndex{33}\)
\((7x)^2\)no es generalmente igual a\(7x^2\)
- Responder
-
Seleccione\(x = 2\). Entonces,\(196 \not = 28\)
Ejercicio\(\PageIndex{34}\)
\((a + b)^2\)no es generalmente igual a\(a^2 + b^2\)
Ejercicio\(\PageIndex{35}\)
Por lo que el número real es\((6a)^2\) igual a\(6a^2\)
- Responder
-
\(0\)
Ejercicio\(\PageIndex{36}\)
Por lo que los números reales,\(a\) y\(b\), es\((a + b)^2\) igual a\(a^2 + b^2\).
Utilice el orden de operaciones para simplificar las cantidades para los siguientes problemas.
Ejercicio\(\PageIndex{37}\)
\(3^2 + 7\)
- Responder
-
\(16\)
Ejercicio\(\PageIndex{38}\)
\(4^3 - 18\)
Ejercicio\(\PageIndex{39}\)
\(5^2 + 2(40)\)
- Responder
-
\(105\)
Ejercicio\(\PageIndex{40}\)
\(8^2 + 3 + 5(2 + 7)\)
Ejercicio\(\PageIndex{41}\)
\(2^5 + 3(8 + 1)\)
- Responder
-
\(59\)
Ejercicio\(\PageIndex{42}\)
\(3^4 + 2^4(1 + 5)^3\)
Ejercicio\(\PageIndex{43}\)
\((6^2 - 4^2) \div 5\)
- Responder
-
\(4\)
Ejercicio\(\PageIndex{44}\)
\(2^2(10 - 2^3)\)
Ejercicio\(\PageIndex{45}\)
\((3^4 - 4^3) \div 17\)
- Responder
-
\(1\)
Ejercicio\(\PageIndex{46}\)
\((4 + 3)^2 + 1 \div (2 \cdot 5\)
Ejercicio\(\PageIndex{47}\)
\((2^4 + 2^5 - 2^3 \cdot 5)^2 \div 4^2\)
- Responder
-
\(4\)
Ejercicio\(\PageIndex{48}\)
\(1^6 + 0^8 + 5^2(2 + 8)^3\)
Ejercicio\(\PageIndex{49}\)
\((7)(16) - 9^2 + 4(1^1 + 3^2)\)
- Responder
-
\(71\)
Ejercicio\(\PageIndex{50}\)
\(\dfrac{2^3 - 7}{5^2}\)
Ejercicio\(\PageIndex{51}\)
\(\dfrac{(1 + 6)^2 + 2}{19}\)
- Responder
-
\(\dfrac{51}{19}\)
Ejercicio\(\PageIndex{52}\)
\(\dfrac{6^2 - 1}{5} + \dfrac{4^3 + (2)(3)}{10}\)
Ejercicio\(\PageIndex{53}\)
\(\dfrac{(2 + 1)^3 + 2^3 + 1^3}{6^2} - \dfrac{15^2 - [2(5)]^2}{5 \cdot 5^2}\)
Ejercicio\(\PageIndex{54}\)
\(\dfrac{6^3 - 2 \cdot 10^2}{2^2} + \dfrac{18(2^3 + 7^2)}{2(19) - 3^3}\)
- Responder
-
\(\dfrac{1070}{11}\)o\(97.27\)
Ejercicios para revisión
Ejercicio\(\PageIndex{55}\)
Usa la notación algebraica para escribir la sentencia “un número dividido por ocho, más cinco, es igual a diez”.
Ejercicio\(\PageIndex{56}\)
Dibuja una línea numérica que se extienda de −5 a 5 y coloque puntos en todos los números reales que sean estrictamente mayores que −3 pero menores o iguales a 2.
- Responder
-
Ejercicio\(\PageIndex{57}\)
¿Cada entero es un número entero?
Ejercicio\(\PageIndex{58}\)
Utilice la propiedad conmutativa de la multiplicación para escribir un número igual al número\(yx\).
- Responder
-
\(xy\)
Ejercicio\(\PageIndex{59}\)
Utilice la propiedad distributiva para expandir\(3(x+6)\).