19.4: Otras técnicas en la resolución de problemas
- Page ID
- 161896
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Combinar técnicas en la resolución de ecuaciones
En las Secciones 5.2 y 5.3 se trabajó con técnicas que implicaban el uso de suma, resta, multiplicación y división para resolver ecuaciones. Podemos combinar estas técnicas para resolver ecuaciones más complicadas. Para ello, es útil recordar que se resuelve una ecuación para una variable en particular cuando todos los demás números y/o letras han sido disociados de ella y está sola en un lado del signo igual. También señalaremos que
Para asociar números y letras utilizamos el orden de las operaciones.
- Multiplicar/dividir
- Añadir/restar
Para deshacer una asociación entre números y letras utilizamos el orden de las operaciones a la inversa.
- Añadir/restar
- Multiplicar/dividir
Conjunto de Muestras A
Resolver\(4x - 7 = 9\) para\(x\).
\ (\ begin {array} {Flushleft}
4x-7&=&9&\ text {Primero, deshaga la asociación entre} x\ text {y} 7. \\
&&&\ text {El} 7\ text {está asociado con} x\ text {por resta.} \\
&&&\ text {Deshacer la asociación agregando} 7\ text {a ambos lados.} \\
4x-7+7&=&9+7\\
4x&=&16&\ text {Ahora, deshaga la asociación entre} x {y} 4. \\
&&&\ text {El} 4\ text {está asociado con} x\ text {por multiplicación.} \\
&&&\ text {Deshacer la asociación dividiendo ambos lados por} 4. \\
\ dfrac {4x} {4} &=&\ dfrac {16} {4}\\
16-7&=&9&\ text {¿Es esto correcto? }\\
x&=&4
\ end {array}\)
Comprobar:
\ (\ begin {array} {Flushleft}
4 (4) -7&=&9&\ text {¿Es correcto?} \\
9&=&9&\ text {Sí, esto es correcto}.
\ end {array}\)
Resolver\(\dfrac{3y}{4}-5=-11\).
\ (\ begin {array} {Flushleft}
\ dfrac {3y} {4} -5&=&-11&-5\ text {está asociado con} y\ text {por resta.} \\
&&&\ text {Deshacer la asociación agregando} 5\ text {a ambos lados}\\
\ dfrac {3y} {4} -5+5&=&-11+5\
\ dfrac {3y} {4} &=&-6&4\ text {está asociado con} y\ text {por división}. \\
&&&\ text {Deshacer la asociación multiplicando ambos lados por} 4. \\
4\ cdot\ dfrac {3y} {4} &=&4 (-6)\\
3y&=&-24&3\ text {está asociado con} y\ text {por multiplicación.} \\
&&&\ text {Deshacer la asociación dividiendo ambos lados por} 3. \\
\ dfrac {3y} {3} &=&\ dfrac {-24} {3}\
\ dfrac {3y} {3} &=&-8\
y&=&-8
\ end {array}\)
Comprobar:
\ (\ begin {array} {Flushleft}
\ dfrac {3 (-8)} {4} -5&=&-11&\ text {¿Es correcto?} \\
\ dfrac {-24} {4} -5&=&-11&\ text {¿Es esto correcto?} \\
-6-5&=&-11&\ text {¿Es esto correcto?} \\
-11&=&-11&\ text {Sí, esto es correcto}
\ end {array}\)
Resolver\(\dfrac{8a}{3b} + 2m = 6m - 5\) para\(a\).
\ (\ begin {array} {Flushleft}
\ dfrac {8a} {3b} +2m&=&6m-5&2m\ text {se asocia con} a\ text {por adición. Deshacer la asociación}\\
&&&\ text {restando} 2m\ text {de ambos lados.} \\
\ dfrac {8a} {3b} +2m-2m&=&6m-5-2m\\
\ dfrac {8a} {3b} &=&4m-5&3b\ text {asociado con} a\ text {por división. Deshacer la asociación}\\
&&&\ text {multiplicando ambos lados por} 3b. \\
(3b) (\ dfrac {8a} {3b}) &=&3b (4m-5)\\
8a&=&12bm-15b&8\ text {se asocia con} a\ text {por multiplicación. Deshacer el}\\
&&&\ text {multiplicación dividiendo ambos lados por} 8. \
\ dfrac {8a} {8} &=&\ dfrac {12bm-15b} {8}\\
a&=&\ dfrac {12bm-15b} {8}
\ end {array}\)
Conjunto de práctica A
Resolver\(3y−1=11\) para\(y\).
- Responder
-
\(y = 4\)
Resolver\(\dfrac{5m}{2} + 6 = 1\) para\(m\).
- Responder
-
\(m=−2\)
Resolver\(2n+3m=4\) para\(n\).
- Responder
-
\(n = \dfrac{4-3m}{2}\)
Resolver\(\dfrac{9k}{2h}+5=p-2\) para\(k\)
- Responder
-
\(k = \dfrac{2hp-14h}{9}\)
En ocasiones a la hora de resolver una ecuación es necesario simplificar las expresiones que la componen.
Conjunto de Muestras B
Resolver\(4x+1-3x = (-2)(4)\) para\(x\).
\ (\ begin {array} {Flushleft}
4x+1-3x&=& (-2) (4)\\
x+1&=&-8\
x&=&-9\\
\ end {array}\)
Comprobar:
\ (\ begin {array} {Flushleft}
4 (-9) +1-3 (-9) &=&-8&\ text {¿Es esto correcto?} \\
-36+1+27&=&-8&\ text {¿Es esto correcto?} \\
-8&=&-8&\ text {Sí, esto es correcto.}
\ end {array}\)
Resolver\(3(m-6)-2m=-4+1\) para\(m\).
\ (\ begin {array} {Flushleft}
3 (m-6) -2m&=&-4+1\\
3m-18-2m&=&-3\\
m-18&=&-3\\
m&=&15
\ end {array}\)
Comprobar:
\ (\ begin {array} {Flushleft}
3 (15-6) -2 (15) &=&-4+1&\ text {¿Es correcto?} \\
3 (9) -30&=&-3&\ text {¿Es esto correcto?} \\
27-30&=&-3&\ text {¿Es esto correcto?} \\
-3&=&-3&\ text {Sí, esto es correcto}
\ end {array}\)
Set de práctica B
Resuelve y comprueba cada ecuación.
\(16x−3−15x=8\)para\(x\).
- Responder
-
\(x=11\)
\(4(y−5)−3y=−1\)para\(y\).
- Responder
-
\(y=19\)
\(-2(a^2+3a-1)+2a^2+7a=0\)para\(a\).
- Responder
-
\(a=−2\)
\(5m(m-2a-1)-5m^2+2a(5m+3)=10\)para\(a\).
- Responder
-
\(a = \dfrac{10+5m}{6}\)
A menudo la variable para la que deseamos resolver aparecerá en ambos lados del signo igual. Podemos aislar la variable en el lado izquierdo o derecho de la ecuación utilizando las técnicas de las Secciones 5.2 y 5.3.
Conjunto de Muestras C
Resolver\(6x-4=2x+8\) para\(x\).
\ (\ begin {array} {Flushleft}
6x-4&=&2x+8&\ text {Para aislar} x\ text {en el lado izquierdo, resta} 2x\ text {de ambos lados.} \\
6x-4-2x&=&2x+8-2x\\
4x-4&=&8&\ text {Agregar} 4\ texto {a ambos lados.} \\
4x-4+4&=&8+4\\
4x&=&12&\ text {Divide ambos lados por} 4\
\\ dfrac {4x} {4} &=&\ dfrac {12} {4}\\
x&=&3
\ end {array}\)
Comprobar:
\ (\ begin {array} {Flushleft}
6 (3) -4&=&2 (3) +8&\ text {¿Es esto correcto?} \\
18-4&=&6+8&\ text {¿Es esto correcto?} \\
14&=&14&\ text {Sí, esto es correcto.}
\ end {array}\)
Resolver\(6(1-3x)+1=2x-[3(x-7)-20]\) para\(x\).
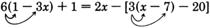
\ (\ begin {array} {Flushleft}
6-18x+1&=&2x- [3x-21-20]\\
-18x+7&=&2x- [3x-41]\
-18x+7&=&2x-3x+41\\
-18x+7&=&-x+41&\ text {Para aislar} x\ text {en el lado derecho, agregue} 18x\ text {ambos lados.} \\
-18x+7+18x&=&-x+41+18x\\
7&=&17x+41&\ text {Restar} 41\ texto {de ambos lados}. \\
7-41&=&17x+41-41\\
-34&=&17x&\ text {Divide ambos lados por} 17. \\
\ dfrac {-34} {17} &=&\ dfrac {17x} {17}\\
-2&=&x&\ text {Desde la ecuación} -2=x\ text {es equivalente a la ecuación}\\
&&&x=-2,\ text {podemos escribir la respuesta como} x=-2. \\
x&=&-2
\ end {array}\)
Comprobar:
\ (\ begin {array} {Flushleft}
6 (1- (3 (-2)) +1&=&2 (-2) - [3 (-2-7) -20] &\ text {¿Es correcto?} \\
6 (1+6) +1&=&−4− [3 (−9) −20] &\ text {¿Es esto correcto?} \\
6 (7) +1&=&-4- [-27-20] &\ text {¿Es esto correcto?} \\
42+1&=&-4- [-47] &\ text {¿Esto es correcto?} \\
43&=&-4+47&\ text {¿Es esto correcto?} \\
43&=&43&\ text {Sí, esto es correcto}\\
\ end {array}\)
Set de práctica C
Resolver\(8a+5=3a−5\) para\(a\).
- Responder
-
\(a=−2\)
Resolver\(9y+3(y+6)=15y+21\) para\(y\).
- Responder
-
\(y=−1\)
Resolver\(3k+2[4(k−1)+3]=63−2k\) para\(k\).
- Responder
-
\(k=5\)
Reconocer identidades y contradicciones
Como señalamos en la Sección 5 .2, algunas ecuaciones son identidades y otras son contradicciones. Como sugieren los problemas del Conjunto de Muestras D,
Reconocer una identidad
- Si, al resolver una ecuación, se eliminan todas las variables y resulta una declaración verdadera, la ecuación es una identidad.
Reconocer una contradicción
- Si, al resolver una ecuación, se eliminan todas las variables y resulta una declaración falsa, la ecuación es una contradicción.
Conjunto de Muestras D
Resolver\(9x + 3(4-3x) = 12\) para\(x\)
\ (\ begin {array} {Flushleft}
9x+12-9x&=&12\\
12&=&12
\ end {array}\)
La variable ha sido eliminada y el resultado es una declaración verdadera. La ecuación original es una identidad.
Resolver\(-2(10-2y)-4y+1=-18\) para\(y\)
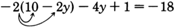
\ (\ begin {array} {Flushleft}
-20+4y-4y+1&=&-18\
-19&=&-18
\ end {array}\)
La variable ha sido eliminada y el resultado es una declaración falsa. La ecuación original es una contradicción.
Set de Práctica D
Clasificar cada ecuación como identidad o contradicción.
\(6x+3(1−2x)=3\)
- Responder
-
identidad,\(3=3\)
\(−8m+4(2m−7)=28\)
- Responder
-
contradicción,\(−28=28\)
\(3(2x−4)−2(3x+1)+14=0\)
- Responder
-
identidad,\(0=0\)
\(−5(x+6)+8=3[4−(x+2)]−2x\)
- Responder
-
contradicción,\(−22=6\)
Ejercicios
Para los siguientes problemas, resolver cada ecuación condicional. Si la ecuación no es condicional, identifíquela como una identidad o una contradicción.
\(3x+1=16\)
- Responder
-
\(x=5\)
\(6y−4=20\)
\(4a−1=27\)
- Responder
-
\(a=7\)
\(3x+4=40\)
\(2y+7=−3\)
- Responder
-
\(y=−5\)
\(8k−7=−23\)
\(5x+6=−9\)
- Responder
-
\(x=−3\)
\(7a+2=−26\)
\(10y−3=−23\)
- Responder
-
\(y=−2\)
\(14x+1=−55\)
\(\dfrac{x}{9} + 2 = 6\)
- Responder
-
\(x=36\)
\(\dfrac{m}{7} - 8 = -11\)
\(\dfrac{y}{4}+6=12\)
- Responder
-
\(y=24\)
\(\dfrac{x}{8}-2=5\)
\(\dfrac{m}{11}-15=-19\)
- Responder
-
\(m=−44\)
\(\dfrac{k}{15}+20=10\)
\(6+\dfrac{k}{5}=5\)
- Responder
-
\(k=−5\)
\(1-\dfrac{n}{2}=6\)
\(\dfrac{7x}{4}+6=-8\)
- Contestar
-
\(x=−8\)
\(\dfrac{-6m}{5}+11=-13\)
\(\dfrac{3k}{14} + 25 = 22\)
- Contestar
-
\(k=-14\)
\(3(x−6)+5=−25\)
\(16(y−1)+11=−85\)
- Contestar
-
\(y=−5\)
\(6x+14=5x−12\)
\(23y−19=22y+1\)
- Contestar
-
\(y=20\)
\(−3m+1=3m−5\)
\(8k+7=2k+1\)
- Contestar
-
\(k=−1\)
\(12n+5=5n−16\)
\(2(x−7)=2x+5\)
- Contestar
-
contradicción
\(−4(5y+3)+5(1+4y)=0\)
\(3x+7=−3−(x+2)\)
- Contestar
-
\(x=−3\)
\(4(4y+2)=3y+2[1−3(1−2y)]\)
\(5(3x−8)+11=2−2x+3(x−4)\)
- Contestar
-
\(x = \dfrac{19}{14}\)
\(12−(m−2)=2m+3m−2m+3(5−3m)\)
\(−4 \cdot k−(−4−3k)=−3k−2k−(3−6k)+1\)
- Contestar
-
\(k = 3\)
\(3[4−2(y+2)]=2y−4[1+2(1+y)]\)
\(−5[2m−(3m−1)]=4m−3m+2(5−2m)+1\)
- Contestar
-
\(m=2\)
Para los siguientes problemas, resolver las ecuaciones literales para la variable indicada. Cuando se le indique, encuentre el valor de esa variable para los valores dados de las otras variables.
Resolver\(I = \dfrac{E}{R}\) para\(R\). Encuentra el valor de\(R\) cuándo\(I = 0.005\) y\(E = 0.0035\).
Resolver\(P = R - C\) para\(R\). Encuentra el valor de\(R\) cuándo\(P = 27\) y\(C = 85\).
- Contestar
-
\(R=112\)
Resolver\(z = \dfrac{x-\hat{x}}{s}\) para\(x\). Encuentra el valor de\(x\) cuándo\(z = 1.96, s = 2.5,\) y\(\hat{x} = 15\).
Resolver\(F = \dfrac{S_{x}^{2}}{S_{y}^{2}}\) para\(S_{x}^{2} \cdot S_{x}^{2}\) representa una sola cantidad. Encuentra el valor de\(S_{x}^{2}\) cuándo\(F = 2.21\) y\(S_{y}^{2} = 3.24\)
- Contestar
-
\(S_{x}^{2} = F \cdot S_{y}^{2}\);\(S_{x}^{2} = 7.1604\)
Resolver\(p = \dfrac{nRT}{V}\) para\(R\)
Resolver\(x=4y+7\) para\(y\).
- Contestar
-
\(y = \dfrac{x-7}{4}\)
Resolver\(y=10x+16\) para\(x\).
Resolver\(2x+5y=12\) para\(y\).
- Contestar
-
\(y = \dfrac{-2x+12}{5}\)
Resolver\(−9x+3y+15=0\) para\(y\).
Resolver\(m = \dfrac{2n-h}{5}\) para\(n\).
- Contestar
-
\(\dfrac{5m+h}{2}\)
Resolver\(t = \dfrac{Q+6P}{8}\) para\(P\).
Ejercicios para la revisión
Simplificar\((x+3)^2(x-2)^3(x-2)^4(x+3)\)
- Contestar
-
\((x+3)^3(x-2)^7\)
Encuentra el producto. \((x-7)(x+7)\)
Encuentra el producto. \((2x-1)^2\).
- Contestar
-
\(4x^2-4x+1\)
Resuelve la ecuación\(y−2=−2\).
Resolver la ecuación\(\dfrac{4x}{5} = -3\)
- Contestar
-
\(x = \dfrac{-15}{4}\)