3.1: De paralelogramos a triángulos

Lección

Comparemos paralelogramos y triángulos.

Ejercicio\(\PageIndex{1}\): Same Parallelograms, Different Bases

Aquí hay dos copias de un paralelogramo. Cada copia tiene un lado etiquetado como base\(b\) y un segmento dibujado para su altura correspondiente y etiquetado\(h\).

Figura\(\PageIndex{1}\)

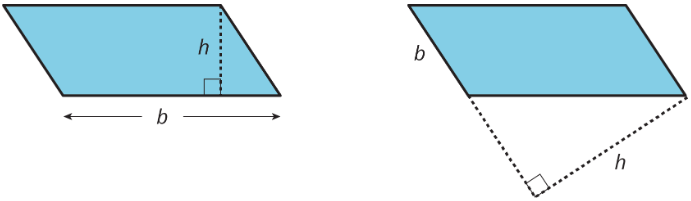
1. La base del paralelogramo a la izquierda es de 2.4 centímetros; su altura correspondiente es de 1 centímetro. Encuentra su área en centímetros cuadrados.
2. La altura del paralelogramo a la derecha es de 2 centímetros. ¿Cuánto dura la base de ese paralelogramo? Explica tu razonamiento.

Ejercicio\(\PageIndex{2}\): A Tale of Two Triangles (Part 1)

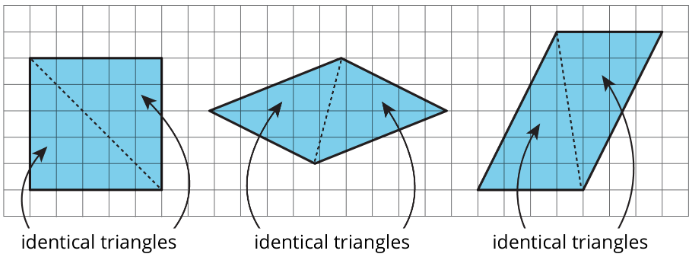
Dos polígonos son idénticos si coinciden exactamente cuando se colocan uno encima del otro.

1. Dibuja una línea para descomponer cada polígono en dos triángulos idénticos, si es posible. Si eliges, también puedes dibujar los triángulos.
2. ¿Qué cuadriláteros se pueden descomponer en dos triángulos idénticos?
   Haga una pausa aquí para una discusión en grupos pequeños.
3. Estudiar los cuadriláteros que, de hecho, eran descomponibles en dos triángulos idénticos. ¿Qué notas de ellos? Escribe un par de observaciones sobre lo que estos cuadriláteros tienen en común.

¿Estás listo para más?

Dibuja algunos otros tipos de cuadriláteros que aún no se muestran. Intenta descomponerlos en dos triángulos idénticos. ¿Puedes hacerlo? Llegar a una regla general sobre lo que debe ser cierto si un cuadrilátero se puede descomponer en dos triángulos idénticos.

Applet GeoGebra XPezQFQP

Ejercicio\(\PageIndex{3}\): A Tale of Two Triangles (Part 2)

Este applet tiene ocho pares de triángulos. Cada miembro del grupo debe elegir 1—2 pares de triángulos. Úselos para ayudarte a responder las siguientes preguntas.

1. 1. ¿Qué par (s) de triángulos tienes?
   2. ¿Se puede componer cada par en un rectángulo? ¿Un paralelogramo?
2. Discuta sus respuestas a la primera pregunta con su grupo. Después, complete cada una de las siguientes declaraciones con todas, algunas o ninguna. Esboce 1—2 ejemplos para ilustrar cada declaración completada.
   1. ________________ de estos pares de triángulos idénticos se pueden componer en un rectángulo.
   2. ________________ de estos pares de triángulos idénticos se pueden componer en un paralelogramo.

Resumen

Un paralelogramo siempre se puede descomponer en dos triángulos idénticos por un segmento que conecta vértices opuestos.

Figura\(\PageIndex{2}\)

Al revés, siempre se pueden disponer dos copias idénticas de un triángulo para formar un paralelogramo, independientemente del tipo de triángulo que se utilice.

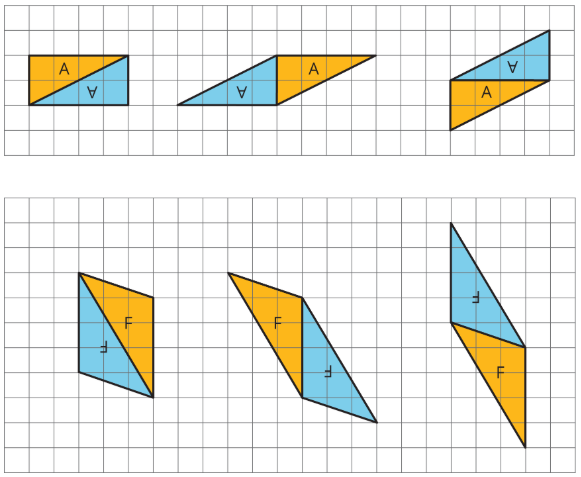
Para producir un paralelogramo, podemos unir un triángulo y su copia a lo largo de cualquiera de los tres lados, por lo que el mismo par de triángulos puede hacer diferentes paralelogramos.

Aquí hay ejemplos de cómo dos copias tanto del Triángulo A como del Triángulo F se pueden componer en tres paralelogramos diferentes.

Figura\(\PageIndex{3}\)

Esta relación especial entre triángulos y paralelogramos puede ayudarnos a razonar sobre el área de cualquier triángulo.

Práctica

Ejercicio\(\PageIndex{4}\)

Para descomponer un cuadrilátero en dos formas idénticas, Clare dibujó una línea discontinua como se muestra en el diagrama.

Figura\(\PageIndex{4}\)

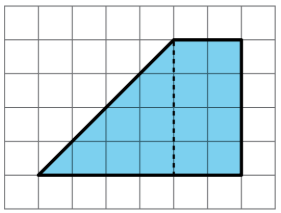
1. Dijo el que dos formas resultantes tienen la misma área. ¿Estás de acuerdo? Explica tu razonamiento.
2. ¿Clare particionó la figura en dos formas idénticas? Explica tu razonamiento.

Ejercicio\(\PageIndex{5}\)

El triángulo R es un triángulo rectángulo. ¿Podemos usar dos copias de Triángulo R para componer un paralelogramo que no es cuadrado?

Figura\(\PageIndex{5}\)

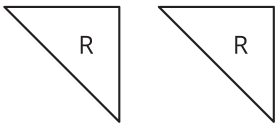
Si es así, explique cómo o esboce una solución. Si no, explica por qué no.

Ejercicio\(\PageIndex{6}\)

Dos copias de este triángulo se utilizan para componer un paralelogramo. ¿Qué paralelogramo no puede ser resultado de la composición? Si te quedas atascado, considera usar papel de calco.

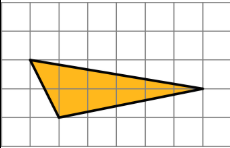
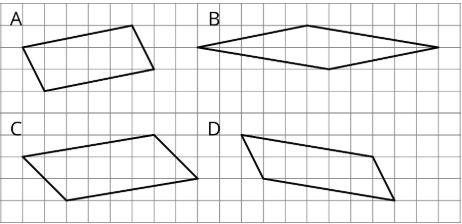
Figura\(\PageIndex{6}\)

Figura\(\PageIndex{7}\)

1. A
2. B
3. C
4. D

Ejercicio\(\PageIndex{7}\)

1. En la cuadrícula, dibuje al menos tres cuadriláteros diferentes que puedan descomponerse cada uno en dos triángulos idénticos con un solo corte (mostrar la línea de corte). Uno o más de los cuadriláteros deben tener ángulos no rectos.

Figura\(\PageIndex{8}\)

2. Identificar el tipo de cada cuadrilátero.

Ejercicio\(\PageIndex{8}\)

1. Un paralelogramo tiene una base de 9 unidades y una altura correspondiente de\(\frac{2}{3}\) unidades. ¿Cuál es su área?
2. Un paralelogramo tiene una base de 9 unidades y un área de 12 unidades cuadradas. ¿Cuál es la altura correspondiente para esa base?
3. Un paralelogramo tiene una superficie de 7 unidades cuadradas. Si la altura que corresponde a una base es\(\frac{1}{4}\) unidad, ¿cuál es la base?

(De la Unidad 1.2.3)

Ejercicio\(\PageIndex{9}\)

Seleccione todos los segmentos que podrían representar la altura si lado\(n\) es la base.

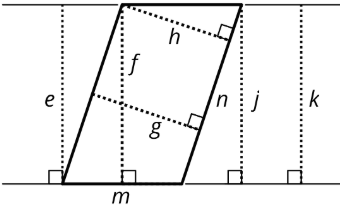
Figura\(\PageIndex{9}\)

1. \(e\)
2. \(f\)
3. \(g\)
4. \(h\)
5. \(m\)
6. \(n\)
7. \(j\)
8. \(k\)

(De la Unidad 1.2.2)