43.2: Encontrar e interpretar la media como punto de equilibrio

Lección

Veamos otra forma de entender la media de un conjunto de datos.

Ejercicio\(\PageIndex{1}\): Which One Doesn't Belong: Division

¿Qué expresión no pertenece? Esté preparado para explicar su razonamiento.

\(\frac{8+8+4+4}{4}\qquad\frac{10+10+4}{4}\qquad\frac{9+9+5+5}{4}\qquad\frac{6+6+6+6+6}{5}\)

Ejercicio\(\PageIndex{2}\): Travel Times (Part 1)

Aquí está el conjunto de datos de una lección anterior que muestra cuánto tiempo le toma a Diego caminar a la escuela, en minutos, más de 5 días. El número medio de minutos es de 11.

\(12\qquad 7\qquad 13\qquad 9\qquad 14\)

1. Representar los datos de Diego en una gráfica de puntos. Marcar la ubicación de la media con un triángulo.
2. La media también puede verse como una medida de centro que equilibra los puntos en un conjunto de datos. Si encontramos la distancia entre cada punto y la media, sumamos las distancias a cada lado de la media, y comparamos las dos sumas, podemos ver este equilibrio.
   1. Registrar la distancia entre cada punto y 11 y su ubicación relativa a 11.

      Mesa\(\PageIndex{1}\)

      tiempo en minutos	distancia desde 11	izquierda de 11 o derecha de 11?
      \(12\)
      \(7\)
      \(13\)
      \(9\)
      \(14\)

   2. Suma de distancias a la izquierda de 11:___________ Suma de distancias a la derecha de 11:___________
      ¿Qué notas de las dos sumas?
3. ¿Puede otro punto que no sea la media producir sumas similares de distancias?
   Investiguemos si 10 puede producir sumas similares a las de 11.
   1. Completa la tabla con la distancia de cada punto de datos desde 10.

      Mesa\(\PageIndex{2}\)

      tiempo en minutos	distancia desde 10	izquierda de 10 o derecha de 10?
      \(12\)
      \(7\)
      \(13\)
      \(9\)
      \(14\)

   2. Suma de distancias a la izquierda de 10:___________ Suma de distancias a la derecha de 10:___________
      ¿Qué notas de las dos sumas?
4. Con base en tu trabajo hasta el momento, explica por qué la media puede considerarse un punto de equilibrio para el conjunto de datos.

Ejercicio\(\PageIndex{3}\): Travel Times (Part 2)

1. Aquí hay diagramas de puntos que muestran cuánto tardaron los viajes de Diego a la escuela en minutos, lo que estudiaste antes, y cuánto tardaron en minutos los viajes de Andre a la escuela. Las gráficas de puntos incluyen las medias para cada conjunto de datos, marcadas por triángulos.

Figura\(\PageIndex{1}\): Dos parcelas de puntos, tiempo de viaje en minutos, de 7 a 22 por unos. La primera parcela, Deigo's, tiene un punto cada uno a las 7, 9, 12, 13, 14 y un triángulo a las 11. La segunda trama, la de Andre, tiene 2 puntos en 12, un punto cada uno a 13, 16, 17 y un triángulo en 1

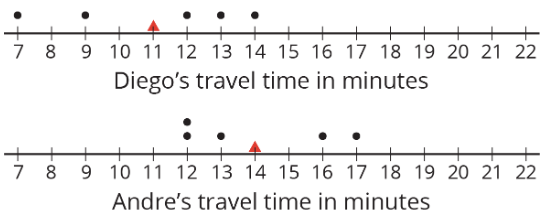
1. ¿Cuál de los dos conjuntos de datos tiene una media mayor? En este contexto, ¿qué nos dice un medio más grande?
2. ¿Cuál de los dos conjuntos de datos tiene mayores sumas de distancias a la izquierda y a la derecha de la media? ¿Qué nos dicen estas sumas sobre la variación en los tiempos de viaje de Diego y Andre?

2. Aquí hay una gráfica de puntos que muestra las longitudes de los viajes de Lin a la escuela.

Figura\(\PageIndex{2}\)

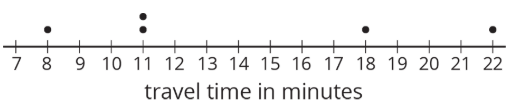
1. Calcular la media de los tiempos de viaje de Lin.
2. Completar la tabla con la distancia entre cada punto y la media así como si el punto está a la izquierda o a la derecha de la media.

   Mesa\(\PageIndex{3}\)

   tiempo en minutos	distancia de la media	izquierda o derecha de la media?
   \(22\)
   \(18\)
   \(11\)
   \(8\)
   \(11\)

3. Encuentra la suma de distancias a la izquierda de la media y la suma de distancias a la derecha de la media.
4. Usa tu trabajo para comparar los tiempos de viaje de Lin con los de Andre ¿Qué puedes decir de sus tiempos promedio de viaje? ¿Qué pasa con la variabilidad en sus tiempos de viaje?

Resumen

La media se usa a menudo como medida del centro de una distribución. Esto se debe a que la media de una distribución puede verse como el “punto de equilibrio” para la distribución. ¿Por qué es esta una buena manera de pensar sobre la media? Veamos un conjunto muy sencillo de datos sobre el número de cookies que cada uno de los ocho amigos horneó:

\(19\qquad 20\qquad 20\qquad 21\qquad 21\qquad 22\qquad 22\qquad 23\)

Aquí hay una gráfica de puntos que muestra el conjunto de datos.

Figura\(\PageIndex{3}\): Gráfica de puntos para “número de cookies”. Se indican los números del 18 al 24. Hay un triángulo indicado en 21 galletas. Los datos son los siguientes: 18 cookies, 0 puntos. 19 cookies, 1 punto. 20 galletas, 2 puntos. 21 galletas, 2 puntos. 22 galletas, 2 puntos. 23 galletas, 1 punto. 24 galletas, 0 puntos.

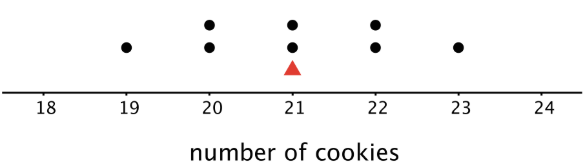
La distribución mostrada es completamente simétrica. El número medio de cookies es 21, porque\((19+20+20+21+21+22+22+23)\div 8=21\). Si marcamos la ubicación de la media en la gráfica de puntos, podemos ver que los puntos de datos podrían equilibrarse en 21.

En esta gráfica, cada punto a cada lado de la media tiene una imagen especular. Por ejemplo, los dos puntos en 20 y los dos en 22 están a la misma distancia de 21, pero cada par se ubica a cada lado de 21. Podemos pensar en ellos como equilibrándose entre sí alrededor de 21.

Figura\(\PageIndex{4}\): Gráfica de puntos para “número de cookies”. Se indican los números del 18 al 24. Hay un triángulo indicado en 21 galletas. Hay flechas que apuntan a los puntos en 20 y 22. Hay líneas que indican la distancia entre 20 y 21 y la distancia entre 21 y 22. Los datos son los siguientes: 18 cookies, 0 puntos. 19 cookies, 1 punto. 20 galletas, 2 puntos. 21 galletas, 2 puntos. 22 galletas, 2 puntos. 23 galletas, 1 punto. 24 galletas, 0 puntos.

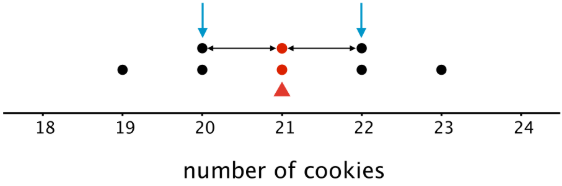
De igual manera, los puntos en 19 y 23 están a la misma distancia de 21 pero están a cada lado del mismo. Ellos, también, pueden verse como equilibrándose entre sí alrededor de 21.

Figura\(\PageIndex{5}\): Gráfica de puntos para “número de cookies”. Se indican los números del 18 al 24. Hay un triángulo indicado en 21 galletas. Hay flechas que apuntan a los puntos en 19 y 23. Hay líneas que indican la distancia entre 19 y 21 y la distancia entre 21 y 23. Los datos son los siguientes: 18 cookies, 0 puntos. 19 cookies, 1 punto. 20 galletas, 2 puntos. 21 galletas, 2 puntos. 22 galletas, 2 puntos. 23 galletas, 1 punto. 24 galletas, 0 puntos.

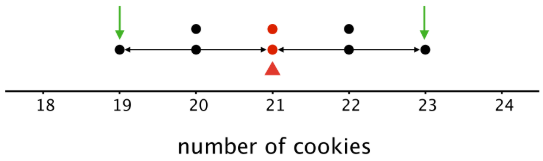
Podemos decir que la distribución de las galletas tiene un centro en 21 porque ese es su punto de equilibrio, y que los ocho amigos, en promedio, hornearon 21 galletas.

Incluso cuando una distribución no es completamente simétrica, las distancias de valores por debajo de la media, en su conjunto, equilibran las distancias de valores por encima de la media.

Entradas en el glosario

Definición: Promedio

El promedio es otro nombre para la media de un conjunto de datos.

Para el conjunto de datos 3, 5, 6, 8, 11, 12, el promedio es 7.5.

\(3+5+6+8+11+12=45\)

\(45\div 6=7.5\)

Definición: Media

La media es una forma de medir el centro de un conjunto de datos. Podemos pensarlo como un punto de equilibrio. Por ejemplo, para el conjunto de datos 7, 9, 12, 13, 14, la media es 11.

Figura\(\PageIndex{6}\)

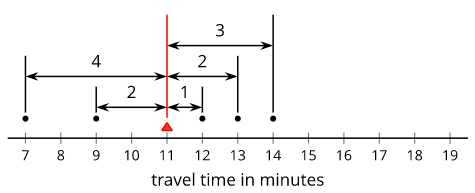
Para encontrar la media, suma todos los números en el conjunto de datos. Entonces, divídalo por cuántos números hay. \(7+9+12+13+14=55\)y\(55\div 5=11\).

Definición: Medida de Centro

Una medida de centro es un valor que parece típico para una distribución de datos.

La media y la mediana son ambas medidas del centro.

Practica

Ejercicio\(\PageIndex{4}\)

En días escolares, Kiran camina a la escuela. Aquí están los periodos de tiempo, en minutos, para los paseos de Kiran en 5 días escolares:

\(16\qquad 11\qquad 18\qquad 12\qquad 13\)

1. Crear una gráfica de puntos para los datos de Kiran.
2. Sin calcular, decidir si 15 minutos serían una buena estimación de la media. Si crees que es una buena estimación, explica tu razonamiento. Si no, da una mejor estimación y explica tu razonamiento.
3. Calcular la media para los datos de Kiran.
4. En la tabla, registre la distancia de cada punto de datos desde la media y su ubicación relativa a la media.

   Mesa\(\PageIndex{4}\)

   tiempo en minutos	distancia de la media	izquierda o derecha de la media?
   \(16\)
   \(11\)
   \(18\)
   \(12\)
   \(13\)

5. Calcular la suma de todas las distancias a la izquierda de la media, luego calcular la suma de distancias a la derecha de la media. Explique cómo estas sumas muestran que la media es un punto de equilibrio para los valores en el conjunto de datos.

Ejercicio\(\PageIndex{5}\)

Noé anotó 20 puntos en un juego. El puntaje de Mai fue de 30 puntos. El puntaje medio para Noé, Mai y Clare fue de 40 puntos. ¿Cuál fue la puntuación de Clare? Explica o muestra tu razonamiento.

Ejercicio\(\PageIndex{6}\)

Compara los números usando >, < o =.

1. \(-2\underline{\qquad} 3\)
2. \(|-12|\underline{\qquad} |15|\)
3. \(3\underline{\qquad} -4\)
4. \(|15|\underline{\qquad} |-12|\)
5. \(7\underline{\qquad} -11\)
6. \(-4\underline{\qquad} |5|\)

(De la Unidad 7.1.7)

Ejercicio\(\PageIndex{7}\)

1. Trama\(\frac{2}{3}\) y\(\frac{3}{4}\) en una recta numérica.
2. ¿Es\(\frac{2}{3}<\frac{3}{4}\), o es\(\frac{3}{4}<\frac{2}{3}\)? Explica cómo sabes.

(De la Unidad 7.1.3)

Ejercicio\(\PageIndex{8}\)

Seleccione todas las expresiones que representen el área total del rectángulo grande.

Figura\(\PageIndex{7}\): Un rectángulo grande está dividido por un segmento de línea vertical en 2 rectángulos más pequeños. El rectángulo izquierdo tiene una longitud lateral vertical de 5 y una longitud lateral horizontal de x El rectángulo derecho tiene una longitud lateral horizontal de y.

1. \(5(x+y)\)
2. \(5+xy\)
3. \(5x+5y\)
4. \(2(5+x+y)\)
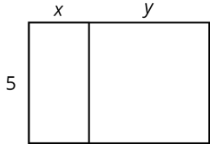
5. \(5xy\)

(De la Unidad 6.2.5)