43.3: Variabilidad y MAD

Última actualización
Guardar como PDF

Page ID: 119926

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Lección

Estudiemos las distancias entre los puntos de datos y la media y veamos qué nos dicen.

Ejercicio\(\PageIndex{1}\): Shooting Hoops (Part 1)

Elena, Jada y Lin disfrutan jugando básquetbol durante el recreo. Últimamente, han estado practicando tiros libres. Registran el número de canastas que hacen de 10 intentos. Aquí están sus conjuntos de datos para 12 días escolares.

Elena

\(4\qquad 5\qquad 1\qquad 6\qquad 9\qquad 7\qquad 2\qquad 8\qquad 3\qquad 3\qquad 5\qquad 7\)

Jada

\(2\qquad 4\qquad 5\qquad 4\qquad 6\qquad 6\qquad 4\qquad 7\qquad 3\qquad 4\qquad 8\qquad 7\)

Lin

\(3\qquad 6\qquad 6\qquad 4\qquad 5\qquad 5\qquad 3\qquad 5\qquad 4\qquad 6\qquad 6\qquad 7\)

Calcula el número medio de canastas que hizo cada jugador, y compara las medias. ¿Qué notas?
¿Qué nos dicen los medios en este contexto?

Ejercicio\(\PageIndex{2}\): Shooting Hoops (Part 2)

Aquí están las parcelas de puntos que muestran el número de canastas que Elena, Jada y Lin hicieron cada una a lo largo de 12 días escolares.

En cada gráfica de puntos, marque la ubicación de la media con un triángulo (\(\Delta\)). Luego, contrasta las distribuciones de la gráfica de puntos. Escribe 2—3 oraciones para describir la forma y la difusión de cada distribución.

Figura\(\PageIndex{1}\): Tres parcelas de puntos, número de canastas realizadas, 0 a 10 por unas. La primera parcela, Elena, que comienza en 1 número de puntos por encima de cada incremento es 1, 1, 2, 1, 2, 1, 2, 1, 1. Segunda parcela, Jada, comenzando en 2 el número de puntos por encima de cada incremento es 1, 1, 4, 1, 2, 2, 1. Tercera parcela, Lin, comenzando en 3 el número de puntos por encima de cada incremento es 2, 2, 3, 4, 1.

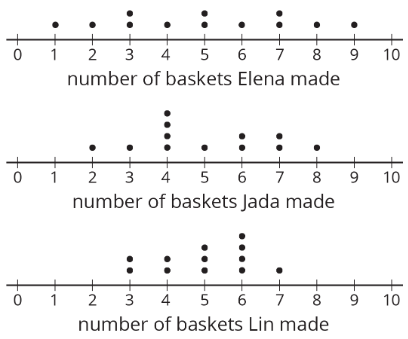
Discuta las siguientes preguntas con su grupo. Explica tu razonamiento.
1. ¿Diría usted que los tres alumnos juegan igual de bien?
2. ¿Diría usted que los tres alumnos juegan igual de manera consistente?
3. Si pudieras elegir a un jugador para estar en tu equipo de basquetbol en base a sus récords, ¿a quién elegirías?

Ejercicio\(\PageIndex{3}\): Shooting Hoops (Part 3)

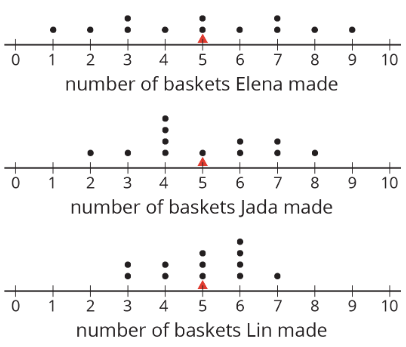
En las mesas se muestran los datos de basquetbol de Elena, Jada y Lin de una actividad anterior. Recordemos que la media de los datos de Elena, así como la de los datos de Jada y Lin, fue de 5.

Registrar la distancia entre cada una de las puntuaciones de Elena y la media.

Mesa\(\PageIndex{1}\)
Elena	\(4\)	\(5\)	\(1\)	\(6\)	\(9\)	\(7\)	\(2\)	\(8\)	\(3\)	\(3\)	\(5\)	\(7\)
distancia desde\(5\)	\(1\)			\(1\)

Ahora encuentra el promedio de las distancias en la tabla. Muestra tu razonamiento y redondea tu respuesta a la décima más cercana.

Este valor es la desviación media absoluta (MAD) de los datos de Elena.

El MAD de Elena: ________

Encuentra la desviación media absoluta de los datos de Jada. Redondearlo a la décima más cercana.

Mesa\(\PageIndex{2}\)
Jada	\(2\)	\(4\)	\(5\)	\(4\)	\(6\)	\(6\)	\(4\)	\(7\)	\(3\)	\(4\)	\(8\)	\(7\)
distancia desde\(5\)

MAD de Jada: _________

Encuentra la desviación absoluta media de los datos de Lin. Redondearlo a la décima más cercana.

Mesa\(\PageIndex{3}\)
Lin	\(3\)	\(6\)	\(6\)	\(4\)	\(5\)	\(5\)	\(3\)	\(5\)	\(4\)	\(6\)	\(6\)	\(7\)
distancia desde\(5\)

El MAD de Lin: _________

Comparar los MADs y las gráficas de puntos de los datos de los tres estudiantes. ¿Ves una relación entre el MAD de cada estudiante y la distribución en su trama de puntos? Explica tu razonamiento.

Figura\(\PageIndex{2}\): Tres parcelas de puntos, número de canastas realizadas, 0 a 10 por unas. La primera parcela, Elena, comenzando en 1 número de puntos por encima de cada incremento es 1, 1, 2, 1, 2, 1, 2, 1, 1, triángulo a 5. Segunda parcela, Jada, comenzando en 2 el número de puntos por encima de cada incremento es 1, 1, 4, 1, 2, 2, 1, triángulo a 5. Tercera parcela, Lin, comenzando en 3 el número de puntos por encima de cada incremento es 2, 2, 3, 4, 1, triángulo a 5.

¿Estás listo para más?

Inventar otro conjunto de datos que también tenga una media de 5 pero que tenga un MAD mayor que 2. Recuerde, los valores en el conjunto de datos deben ser números enteros del 0 al 10.

Ejercicio\(\PageIndex{4}\): Game of 22

Tu profesor le dará a tu grupo una baraja de cartas. Baraja las cartas y coloca la baraja boca abajo sobre la superficie de juego.

Para jugar: Dibuja 3 cartas y suma los valores. Un as es un 1. Un jota, una reina y un rey valen 10 cada uno. Cada una de las tarjetas 2—10 vale su valor nominal. Si su suma es otra cosa que no sea 22 (ya sea por encima o por debajo de 22), diga: “Mi suma se desvió de 22 por ____” , o “Mi suma fue de 22 por ____”.
Para mantener la puntuación: Registre cada suma y cada distancia de 22 en la tabla. Después de cinco rondas, calcula el promedio de las distancias. El jugador con la distancia promedio más baja de 22 gana el juego.

Mesa\(\PageIndex{4}\)
jugador A	ronda 1	ronda 2	ronda 3	ronda 4	ronda 5
suma de tarjetas
distancia desde 22

Distancia promedio desde 22: ____________

Mesa\(\PageIndex{5}\)
jugador B	ronda 1	ronda 2	ronda 3	ronda 4	ronda 5
suma de tarjetas
distancia desde 22

Distancia promedio desde 22: ____________

Mesa\(\PageIndex{6}\)
jugador C	ronda 1	ronda 2	ronda 3	ronda 4	ronda 5
suma de tarjetas
distancia desde 22

Distancia promedio desde 22: ____________

¿Cuya distancia promedio de 22 es la más pequeña? ¿Quién ganó el juego?

Resumen

Usamos la media de un conjunto de datos como medida del centro de su distribución, pero dos conjuntos de datos con la misma media podrían tener distribuciones muy diferentes.

Esta gráfica de puntos muestra los pesos, en gramos, de 22 galletas.

Figura\(\PageIndex{3}\): Una gráfica de puntos para “pesos de galletas en gramos”. Se indican los números del 8 al 34, en incrementos de 2. Se indica un triángulo a 21 gramos. Los datos son los siguientes: 18 gramos, 1 punto; 19 gramos, 3 puntos; 20 gramos, 4 puntos; 21 gramos, 5 puntos; 22 gramos, 6 puntos; 23 gramos, 2 puntos, 24 gramos, 1 punto.

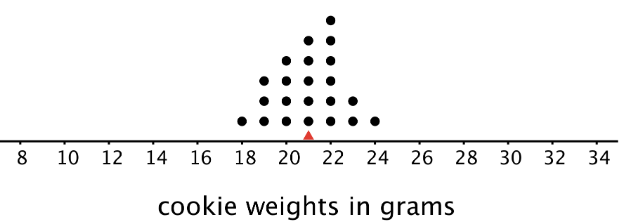
El peso medio es de 21 gramos. Todos los pesos están dentro de los 3 gramos de la media, y la mayoría de ellos están aún más cerca. Estas galletas son todas bastante cercanas en peso.

Esta gráfica de puntos muestra los pesos, en gramos, de un conjunto diferente de 30 galletas.

Figura\(\PageIndex{4}\): Una gráfica de puntos para “pesos de galletas en gramos”. Se indican los números del 8 al 34, en incrementos de 2. Se indica un triángulo a 21 gramos. Los datos son los siguientes: 9 gramos, 1 punto; 10 gramos, 1 punto; 11 gramos, 2 puntos; 12 gramos, 1 punto; 14 gramos, 1 punto; 16 gramos, 2 puntos; 17 gramos, 1 punto; 18 gramos, 2 puntos; 19 gramos, 1 punto; 20 gramos, 3 puntos; 21 gramos, 1 punto; 22 gramos, 3 puntos; 23 gramos, 1 punto; 24 gramos, 2 puntos; 26 gramos, 2 puntos; 28 gramos, 1 punto; 30 gramos, 1 punto; 32 gramos, 2 puntos; 33 gramos, 1 punto; 34 gramos, 1 punto.

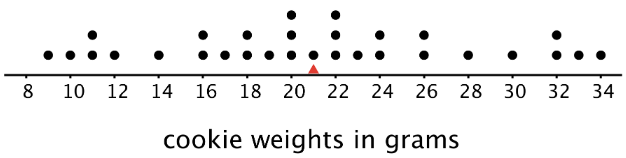
El peso medio para este conjunto de galletas también es de 21 gramos, pero algunas galletas tienen la mitad de ese peso y otras son una vez y media ese peso. Hay mucha más variabilidad en el peso.

Hay un número que podemos usar para describir qué tan lejos, o qué tan dispersos, los puntos de datos generalmente están de la media. Esta medida de propagación se denomina desviación media absoluta (MAD).

Aquí el MAD nos dice hasta qué punto suelen estar los pesos de las galletas de 21 gramos. Para encontrar el MAD, encontramos la distancia entre cada valor de datos y la media, para luego calcular la media de esas distancias.

Por ejemplo, el punto que representa 18 gramos está a 3 unidades de distancia de la media de 21 gramos. Podemos encontrar la distancia entre cada punto y la media de 21 gramos y organizar las distancias en una tabla, como se muestra.

Figura\(\PageIndex{5}\): Una gráfica de puntos para “pesos de galletas en gramos”. Se indican los números del 8 al 34, en incrementos de 2. Se indica un triángulo a 21 gramos. Se dibujan dos líneas perpendiculares, una a 18 gramos y la otra a 21 gramos. Una línea horizontal entre las dos líneas está etiquetada con 3. Los datos son los siguientes: 18 gramos, 1 punto; 19 gramos, 3 puntos; 20 gramos, 4 puntos; 21 gramos, 5 puntos; 22 gramos, 6 puntos; 23 gramos, 2 puntos, 24 gramos, 1 punto.

Mesa\(\PageIndex{7}\)
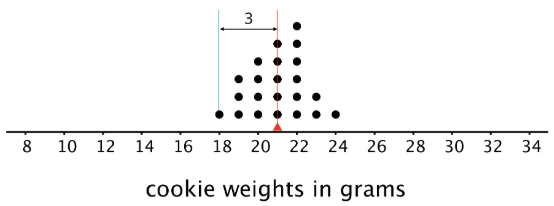
peso en gramos	\(18\)	\(19\)	\(19\)	\(19\)	\(20\)	\(20\)	\(20\)	\(20\)	\(21\)	\(21\)	\(21\)	\(21\)	\(21\)	\(22\)	\(22\)	\(22\)	\(22\)	\(22\)	\(22\)	\(23\)	\(23\)	\(24\)
distancia desde la media	\(3\)	\(2\)	\(2\)	\(2\)	\(1\)	\(1\)	\(1\)	\(1\)	\(0\)	\(0\)	\(0\)	\(0\)	\(0\)	\(1\)	\(1\)	\(1\)	\(1\)	\(1\)	\(1\)	\(2\)	\(2\)	\(3\)

Los valores en la primera fila de la tabla son los pesos de las cookies para el primer conjunto de cookies. Su media, 21 gramos, es la media de los pesos de las galletas.

Los valores en la segunda fila de la tabla son las distancias entre los valores de la primera fila y 21. La media de estas distancias es la MAD de los pesos de las galletas.

¿Qué podemos aprender de los promedios de estas distancias una vez calculadas?

En el primer conjunto de cookies, las distancias están todas entre 0 y 3. El MAD es de 1.2 gramos, lo que nos indica que los pesos de las galletas suelen estar dentro de los 1.2 gramos de 21 gramos. Podríamos decir que una galleta típica pesa entre 19.8 y 22.2 gramos.
En el segundo conjunto de cookies, las distancias están todas entre 0 y 13. El MAD es de 5.6 gramos, lo que nos indica que los pesos de las galletas suelen estar dentro de los 5.6 gramos de 21 gramos. Podríamos decir que una galleta típica pesa entre 15.4 y 26.6 gramos.

El MAD también se llama una medida de la variabilidad de la distribución. En estos ejemplos, es fácil ver que una mayor MAD sugiere una distribución que está más extendida, mostrando más variabilidad.

Entradas en el glosario

Definición: Promedio

El promedio es otro nombre para la media de un conjunto de datos.

Para el conjunto de datos 3, 5, 6, 8, 11, 12, el promedio es 7.5.

\(3+5+6+8+11+12=45\)

\(45\div 6=7.5\)

Definición: Media

La media es una forma de medir el centro de un conjunto de datos. Podemos pensarlo como un punto de equilibrio. Por ejemplo, para el conjunto de datos 7, 9, 12, 13, 14, la media es 11.

Para encontrar la media, suma todos los números en el conjunto de datos. Entonces, divídalo por cuántos números hay. \(7+9+12+13+14=55\)y\(55\div 5=11\).

Definición: Desviación Media Absoluta (MAD)

La desviación absoluta media es una forma de medir qué tan extendido está un conjunto de datos. A veces a esto lo llamamos el MAD. Por ejemplo, para el conjunto de datos 7, 9, 12, 13, 14, el MAD es 2.4. Esto nos dice que estos tiempos de viaje suelen estar a 2.4 minutos de distancia de la media, que es 11.

Para encontrar el MAD, sumar la distancia entre cada punto de datos y la media. Entonces, divídalo por cuántos números hay.

\(4+2+1+2+3=12\)y\(12\div 5=2.4\)

Definición: Medida de Centro

Una medida de centro es un valor que parece típico para una distribución de datos.

La media y la mediana son ambas medidas del centro.

Practica

Ejercicio\(\PageIndex{5}\)

Han grabó el número de páginas que leía cada día durante cinco días. La gráfica de puntos muestra sus datos.

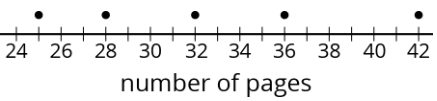
¿30 páginas son una buena estimación del número medio de páginas que Han lee cada día? Explica tu razonamiento.
Encuentra el número medio de páginas que Han leyó durante los cinco días. Dibuja un triángulo para marcar la media en la gráfica de puntos.

Utilice la gráfica de puntos y la media para completar la tabla.

Mesa\(\PageIndex{8}\)
número de páginas	distancia desde la media	izquierda o derecha de la media
\(25\)		izquierda
\(28\)
\(32\)
\(36\)
\(42\)

Calcular la desviación media absoluta (MAD) de los datos. Explica o muestra tu razonamiento.

Ejercicio\(\PageIndex{6}\)

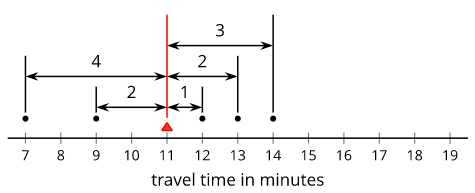
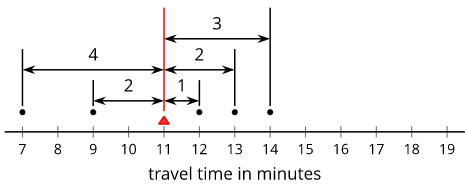
Diez estudiantes de sexto grado registraron las cantidades de tiempo que cada uno tardó en viajar a la escuela. La trama de puntos muestra sus tiempos de viaje.

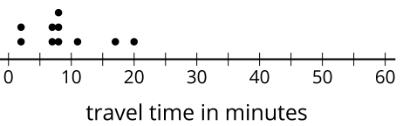
El tiempo medio de viaje para estos estudiantes es de aproximadamente 9 minutos. El MAD es de aproximadamente 4.2 minutos.

¿Cuál es el número de minutos, 9 o 4.2, una cantidad típica de tiempo para que los diez estudiantes de sexto grado viajen a la escuela? Explica tu razonamiento.
Con base en la media y MAD, Jada cree que los tiempos de viaje entre 5 y 13 minutos son comunes para este grupo. ¿Estás de acuerdo? Explica tu razonamiento.
Un grupo diferente de diez estudiantes de sexto grado también registró sus tiempos de viaje a la escuela. Su tiempo medio de viaje también fue de 9 minutos, pero el MAD fue de unos 7 minutos. ¿Cuál podría ser la gráfica de puntos de este segundo conjunto de datos? Describa o dibuje cómo podría verse.

Ejercicio\(\PageIndex{7}\)

En una competencia de tiro con arco, las puntuaciones para cada ronda se calculan promediando la distancia de 3 flechas desde el centro del objetivo.

Un arquero tiene una distancia media de 1.6 pulgadas y una distancia MAD de 1.3 pulgadas en la primera ronda. En la segunda vuelta, las flechas del arquero están más alejadas del centro pero son más consistentes. ¿Qué valores para la media y MAD se ajustarían a esta descripción para la segunda vuelta? Explica tu razonamiento.