44.2: Comparando Media y Mediana

Lección

Comparemos la media y la mediana de los conjuntos de datos.

Ejercicio\(\PageIndex{1}\): Heights of Presidents

Aquí hay dos parcelas de puntos. La primera gráfica de puntos muestra las alturas de los primeros 22 presidentes de Estados Unidos. La segunda trama de puntos muestra las alturas de los próximos 22 presidentes.

Figura\(\PageIndex{1}\): Dos parcelas de puntos de 162 a 194 por 2's. Altura en centímetros. Trama de puntos superior etiquetada como presidentes 1st-22nd. Parcela de puntos inferior etiquetada como presidentes 23rd-44th. Gráfico de puntos superiores comenzando en 162, el número de puntos por encima de cada incremento es 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 4, 1, 1, 0, 0, 2, 0, 1, 0, 0, 4, 0, 1, 0, 1, 0, 2, 1, 0, 0, 0, 0, 1, 0. Gráfico de punto inferior, el número de puntos por encima de cada incremento es 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 2, 1, 3, 0, 3, 0, 2, 0, 0, 3, 0, 3, 0, 0, 0, 1, 0, 1, 0, 0.

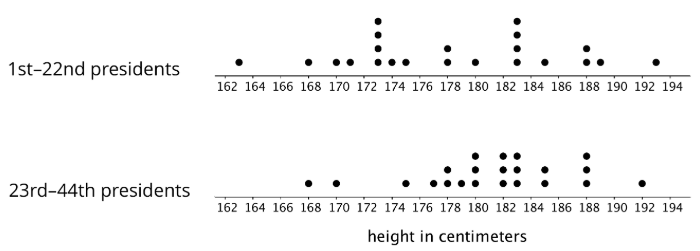
Con base en las dos gráficas de puntos, decida si está de acuerdo o no está de acuerdo con cada una de las siguientes declaraciones. Esté preparado para explicar su razonamiento.

1. La mediana de la estatura de los primeros 22 presidentes es de 178 centímetros.
2. La altura media de los primeros 22 presidentes es de unos 183 centímetros.
3. Una estatura típica para un presidente del segundo grupo es de unos 182 centímetros.
4. Los presidentes estadounidenses se han vuelto más altos con el tiempo.
5. Las alturas de los primeros 22 presidentes son más similares que las alturas de los segundos 22 presidentes.
6. El MAD del segundo conjunto de datos es mayor que el MAD del primer conjunto.

Ejercicio\(\PageIndex{2}\): The Tallest and the Smallest in the World

Tu profesor te proporcionará los datos de estatura para tu clase. Utilice los datos para completar las siguientes preguntas.

1. Encuentra la altura media de tu clase en centímetros.
2. Encuentra la mediana de altura en centímetros. Muestra tu razonamiento.
3. Supongamos que el adulto más alto del mundo, que mide 251 centímetros de altura, se incorporó a su clase.
   1. Discuta las siguientes preguntas con su grupo y explique su razonamiento.
      • ¿Cómo cambiaría la altura media de la clase?
      • ¿Cómo cambiaría la mediana de la estatura?
   2. Encuentra la nueva media.
   3. Encuentra la nueva mediana.
   4. ¿Qué medida de centro, la media o la mediana, cambió más cuando esta nueva persona se unió a la clase? Explique por qué el valor de una medida cambió más que la otra.
4. El adulto más pequeño del mundo mide 63 centímetros de altura. Supongamos que tanto los adultos más altos como los más pequeños del mundo se unieron a tu clase.
   1. Discuta las siguientes preguntas con su grupo y explique su razonamiento.
      • ¿Cómo cambiaría la altura media de la clase con respecto a la media original?
      • ¿Cómo cambiaría la mediana de la estatura con respecto a la mediana original?
   2. Encuentra la nueva media.
   3. Encuentra la nueva mediana.
   4. ¿Cómo cambiaron las medidas del centro, la media y la mediana, cuando estas dos personas se unieron a la clase? Explique por qué los valores de la media y la mediana cambiaron la forma en que lo hicieron.

Ejercicio\(\PageIndex{3}\): Mean or Median?

1. Tu profesor te dará seis tarjetas. Cada uno tiene una gráfica de puntos o un histograma. Clasifique las cartas en dos pilas según las distribuciones mostradas. Esté preparado para explicar su razonamiento.
2. Discuta sus decisiones de clasificación con otro grupo. ¿Tenías las mismas cartas en cada pila? Si es así, ¿usaste las mismas categorías de clasificación? Si no, ¿en qué se diferencian tus categorías?
   Haga una pausa aquí para una discusión en clase.
3. Utilice la información de las tarjetas para responder a las siguientes preguntas.
   1. Tarjeta A: ¿Cuál es la edad típica de los perros tratados en la clínica de animales?
   2. Tarjeta B: ¿Cuál es un número típico de personas en los hogares irlandeses?
   3. Tarjeta C: ¿Cuál es un tiempo de viaje típico para los estudiantes neozelandeses?
   4. Tarjeta D: ¿Sería de 15 años una buena descripción de una edad típica de las personas que acudieron a la fiesta de cumpleaños?
   5. Tarjeta E: ¿Son 15 minutos o 24 minutos una mejor descripción de un tiempo típico que tardan los alumnos en Sudáfrica en llegar a la escuela?
   6. Tarjeta F: ¿Sería de 21.3 años una buena descripción de una edad típica de las personas que se fueron de excursión a Washington, D.C.?
4. ¿Cómo decidiste qué medida de centro usar para las gráficas de puntos en las Tarjetas A—C? ¿Y para los que están en las Tarjetas D — F?

¿Estás listo para más?

La mayoría de los maestros utilizan la media para calcular la calificación final de un estudiante, basándose en los puntajes de ese estudiante en exámenes, cuestionarios, tareas, proyectos y otras tareas calificadas.

Diego piensa que la mediana podría ser una mejor manera de medir qué tan bien le fue a un estudiante en un curso. ¿Estás de acuerdo con Diego? Explica tu razonamiento.

Resumen

Tanto la media como la mediana son formas de medir el centro de una distribución. Nos dicen cosas ligeramente diferentes, sin embargo.

La gráfica de puntos muestra los pesos de 30 galletas. El peso medio es de 21 gramos (marcados con un triángulo). El peso medio es de 20.5 gramos (marcado con un diamante).

Figura\(\PageIndex{2}\)

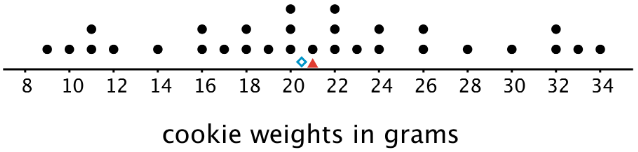
La media nos dice que si los pesos de todas las galletas se distribuyeran de manera que cada una pesara igual, ese peso sería de 21 gramos. También podríamos pensar en 21 gramos como punto de equilibrio para los pesos de todas las galletas del set.

La mediana nos dice que la mitad de las galletas pesan más de 20.5 gramos y la mitad pesan menos de 20.5 gramos. En este caso, tanto la media como la mediana podrían describir un peso típico de las cookies porque están bastante cerca entre sí y de la mayoría de los puntos de datos.

Aquí hay un conjunto diferente de 30 cookies. Tiene el mismo peso medio que el primer conjunto, pero el peso medio es de 23 gramos.

Figura\(\PageIndex{3}\)

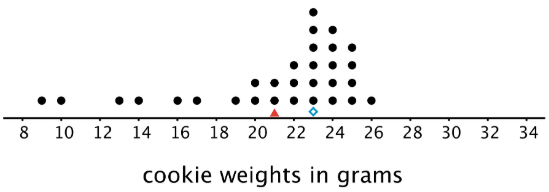
En este caso, la mediana está más cerca de donde se agrupan la mayoría de los puntos de datos y, por lo tanto, es una mejor medida del centro para esta distribución. Es decir, es una mejor descripción de un peso típico de galleta. El peso medio está influenciado (en este caso, tirado hacia abajo) por un puñado de cookies mucho más pequeñas, por lo que está más lejos de la mayoría de los puntos de datos.

En general, cuando una distribución es simétrica o aproximadamente simétrica, los valores medios y medianos son cercanos. Pero cuando una distribución no es más o menos simétrica, los dos valores tienden a estar más separados.

Entradas en el glosario

Definición: Mediana

La mediana es una forma de medir el centro de un conjunto de datos. Es el número medio cuando el conjunto de datos se enumera en orden.

Para el conjunto de datos 7, 9, 12, 13, 14, la mediana es 12.

Para el conjunto de datos 3, 5, 6, 8, 11, 12, hay dos números en el medio. La mediana es el promedio de estos dos números. \(6+8=14\)y\(14\div 2=7\).

Práctica

Ejercicio\(\PageIndex{4}\)

Aquí hay una trama de puntos que muestra las edades de los maestros en una escuela.

¿Cuál de estas afirmaciones es verdadera del conjunto de datos que se muestra en la gráfica de puntos?

Figura\(\PageIndex{4}\)

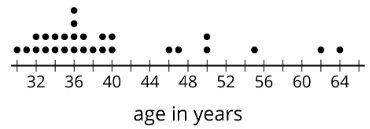
1. La media es menor que la mediana.
2. La media es aproximadamente igual a la mediana.
3. La media es mayor que la mediana.
4. No se puede determinar la media.

Ejercicio\(\PageIndex{5}\)

Priya pidió a cada uno de los cinco amigos que intentaran lanzar una pelota en un bote de basura hasta que lo lograran. Registró el número de intentos infructuosos realizados por cada amiga como: 1, 8, 6, 2, 4. Priya cometió un error: El 8 en el conjunto de datos debería haber sido 18.

¿Cómo afectaría el cambio del 8 al 18 la media y mediana del conjunto de datos?

1. La media disminuiría y la mediana no cambiaría.
2. La media aumentaría y la mediana no cambiaría.
3. La media disminuiría y la mediana aumentaría.
4. La media aumentaría y la mediana aumentaría.

Ejercicio\(\PageIndex{6}\)

En su clase de historia, los puntajes de Han son:

\(100\qquad 100\qquad 100\qquad 100\qquad 95\qquad 100\qquad 90\qquad 100\qquad 0\)

El profesor de historia utiliza la media para calcular la calificación de la tarea. Escriba un argumento para que Han explique por qué la mediana sería una mejor medida para usar en sus calificaciones de tarea.

Ejercicio\(\PageIndex{7}\)

Las gráficas de puntos muestran cuánto tiempo, en minutos, los alumnos de una clase tardaron en completar cada una de cinco tareas diferentes. Seleccione todas las gráficas de puntos de las tareas para las que el tiempo medio sea aproximadamente igual al tiempo medio.

Figura\(\PageIndex{5}\): Cinco gráficas de puntos etiquetadas A, B, C, D y E. En cada gráfica de puntos, se indican los números del 0 al 60, en incrementos de 5. Los datos para la gráfica de puntos A son los siguientes: 2, 1 punto. 3, 2 puntos. 7, 1 punto. 8, 1 punto. 10, 1 punto. 11, 2 puntos. 13, 2 puntos. 15, 1 punto. 18, 1 punto. 19, 2 puntos. 20, 1 punto. 22, 1 punto. 29, 2 puntos. 36, 2 puntos. 37, 1 punto. 38, 1 punto. 40, 1 punto.. 57, 1 punto. 60, 1 punto. Los datos para la gráfica de puntos B son los siguientes: 31, 1 punto. 32, 2 puntos. 33, 3 puntos. 34, 2 puntos. 35, 5 puntos. 36, 3 puntos. 37, 2 puntos. 38, 2 puntos. 39, 2 puntos. 40, 1 punto. 41, 1 punto. 44, 1 punto. 44, 1 punto. Los datos para la gráfica de puntos C son los siguientes: 4, 3 puntos. 5, 3 puntos. 6, 1 punto. 7, 3 puntos. 8, 6 puntos. 9, 2 puntos. 10, 1 punto. 11, 4 puntos. 12, 2 puntos. Los datos para la gráfica de puntos D son los siguientes: 2, 2 puntos. 3, 2 puntos. 4, 3 puntos. 7, 1 punto. 9, 2 puntos. 11, 1 punto. 12, 2 puntos. 14, 2 puntos. 15, 1 punto. 19, 1 punto. 20, 1 punto. 21, 1 punto. 22, 1 punto. 31, 1 punto. 43, 1 punto. 45, 1 punto. 49, 1 punto. 49, 1 punto.. 60, 1 punto. Los datos para la gráfica de puntos E son los siguientes: 3, 4 puntos. 4, 4 puntos. 6, 1 punto. 7, 1 punto. 9, 4 puntos. 10, 3 puntos. 14, 1 punto. 16, 1 punto. 18, 1 punto. 20, 1 punto. 27, 1 punto. 36, 1 punto. 44, 1 punto. 44, 1 punto.

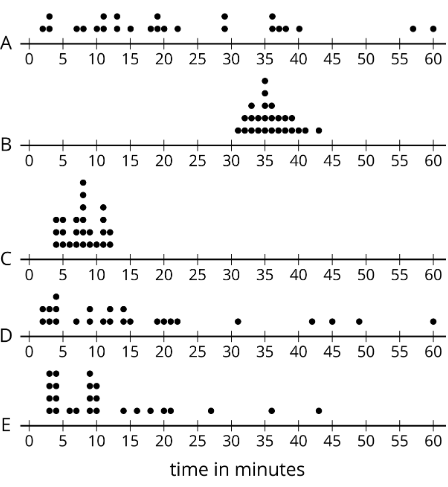
Ejercicio\(\PageIndex{8}\)

Los cuidadores del zoológico registraron las edades, pesos, géneros y alturas de los 10 pandas en su zoológico. Escribir dos preguntas estadísticas que puedan ser respondidas usando estos conjuntos de datos.

(De la Unidad 8.1.2)

Ejercicio\(\PageIndex{9}\)

Aquí hay un conjunto de coordenadas. Dibuja y etiqueta un par de ejes apropiados y trazar los puntos. \(A=(1,0), B=(0,0.5), C=(4,3.5), D=(1.5, 0.5)\)

(De la Unidad 7.3.2)