44.3: Cuartiles y Rango Intercuartil

Lección

Veamos otras medidas para describir distribuciones.

Ejercicio\(\PageIndex{1}\): Notice and Wonder: Two Parties

Aquí hay parcelas de puntos que muestran las edades de las personas en dos fiestas diferentes. La media de cada distribución está marcada con un triángulo.

Figura\(\PageIndex{1}\): Dos parcelas de puntos de 5 a 45 por 5 años. Edad en años. Gráfico de puntos superior conjunto de datos etiquetados A. Gráfico de puntos inferior conjunto de datos etiquetados B. Hay un triángulo rojo indicado en 15 en “conjunto de datos A” y a 20 en “conjunto de datos B”. Los datos para “conjunto de datos A” son los siguientes: 8 años, 12 puntos. 10 años, 3 puntos. 12 años, 1 punto. 15 años, triángulo rojo. 36 años, 1 punto. 42 años, 1 punto. 44 años, 2 puntos. Los datos para “conjunto de datos B” son los siguientes: 7 años, 1 punto. 8 años, 1 punto. 9 años, 1 punto. 10 años, 2 puntos. 15 años, 1 punto. 16 años, 1 punto. 20 años, 2 puntos y 1 triángulo rojo. 22 años, 1 punto. 23 años, 1 punto. 24 años, 1 punto. 28 años, 1 punto. 30 años, 1 punto. 33 años, 1 punto. 33 años, 1 punto. 35 años, 1 punto. 38 años, 1 punto. 42 años, 1 punto.

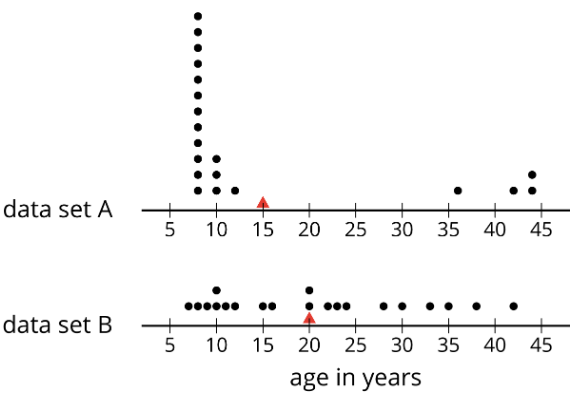
¿Qué notas y qué te preguntas de las distribuciones en las dos parcelas de puntos?

Ejercicio\(\PageIndex{2}\): The Five-Number Summary

Aquí están las edades de las personas en una fiesta, listadas de menor a mayor.

\(7\qquad 8\qquad 9\qquad 10\qquad 10\qquad 11\qquad 12\qquad 15\qquad 16\qquad 20\qquad 20\qquad 22\qquad 23\qquad 24\qquad 28\qquad 30\qquad 33\qquad 35\qquad 38\qquad 42\)

1. 1. Encuentre la mediana del conjunto de datos y etiquételo como “percentil 50”. Esto divide los datos en una mitad superior y una mitad inferior.
   2. Encuentra el valor medio de la mitad inferior de los datos, sin incluir la mediana. Etiquete este valor como “percentil 25”.
   3. Encuentra el valor medio de la mitad superior de los datos, sin incluir la mediana. Etiquete este valor como “percentil 75”.
2. Ha dividido el conjunto de datos en cuatro partes. Cada uno de los tres valores que dividen los datos se denomina cuartil.
   • Llamamos al percentil 25 el primer cuartil. Escribe “Q1” junto a ese número.
   • La mediana se puede llamar el segundo cuartil. Escribe “Q2” junto a ese número.
   • Llamamos al percentil 75 el tercer cuartil. Escribe “Q3” junto a ese número.
3. Etiquete el valor más bajo en el conjunto “mínimo” y el mayor valor “máximo”.
4. Los valores que has identificado conforman el resumen de cinco números para el conjunto de datos. Grabe aquí.
   mínimo: _____ Q1: _____ Q2: _____ Q3: _____ máximo: _____
5. La mediana de este conjunto de datos es 20. Esto nos dice que la mitad de las personas en la fiesta tenían 20 años o menos, y la otra mitad tenían 20 o más. ¿Qué nos dice cada uno de estos otros valores sobre las edades de la gente en la fiesta?
   1. el tercer cuartil
   2. el mínimo
   3. el máximo

¿Estás listo para más?

Hubo otra fiesta donde asistieron 21 personas. Aquí está el resumen de cinco números de sus edades.

mínimo: 5 Q1: 6 Q2: 27 Q3: 32 máximo: 60

1. ¿Crees que esta fiesta tuvo más hijos o menos hijos que la anterior? Explica tu razonamiento.
2. ¿Había más niños o adultos en esta fiesta? Explica tu razonamiento.

Ejercicio\(\PageIndex{3}\): Range and Interquartile Range

1. Aquí hay una trama de puntos que muestra la duración de los viajes en autobús de Elena a la escuela, más de 12 días.

Figura\(\PageIndex{2}\)

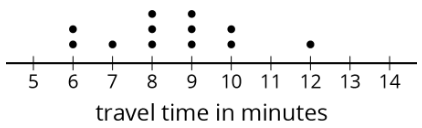
Escriba el resumen de cinco números para este conjunto de datos. Muestra tu razonamiento.

2. El rango es una forma de describir la dispersión de valores en un conjunto de datos. Es la diferencia entre el máximo y el mínimo. ¿Cuál es el rango de los tiempos de viaje de Elena?
3. Otra forma de describir la dispersión de valores en un conjunto de datos es el rango intercuartílico (IQR). Es la diferencia entre el cuartil superior y el cuartil inferior.

1. ¿Cuál es el rango intercuartil (IQR) de los tiempos de viaje de Elena?
2. ¿Qué fracción de los valores de los datos se encuentran entre los cuartiles inferior y superior?

4. Aquí hay dos parcelas de puntos más.

Figura\(\PageIndex{3}\): Dos gráficas de puntos de 14 a 28 por 2's. Gráfica de puntos superior etiquetada conjunto de datos A. Gráfica de puntos inferior etiquetada conjunto de datos B. Gráfica de puntos superior que comienza en 14, el número de puntos por encima de cada incremento de 1 es 0, 1, 3, 1, 0, 0, 3, 1, 2, 3, 4, 1, 3, 1. Gráfico de punto inferior que comienza en 14, el número de puntos por encima de cada incremento de 1 es 0, 0, 0, 0, 0, 0, 0, 0, 0, 3, 3, 8, 2, 6, 3.

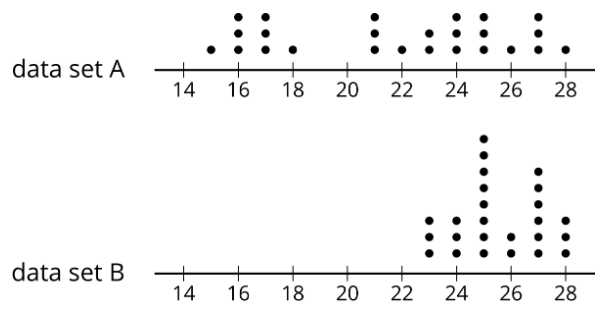
Sin hacer ningún cálculo, predice:

1. ¿Qué conjunto de datos tiene el rango más pequeño?
2. ¿Qué conjunto de datos tiene el IQR más pequeño?

5. Consulta tus predicciones calculando el rango y el IQR para los datos en cada gráfica de puntos.

Resumen

Anteriormente aprendimos que la media es una medida del centro de una distribución y el MAD es una medida de la variabilidad (o propagación) que va con la media. También hay una medida de propagación que va con la mediana. Se llama rango intercuartílico (IQR).

Encontrar el IQR implica dividir un conjunto de datos en cuartos. Cada uno de los tres valores que divide los datos en cuartos se llama cuartil.

• La mediana, o segundo cuartil (Q2), divide los datos en dos mitades.
• El primer cuartil (Q1) es el valor medio de la mitad inferior de los datos.
• El tercer cuartil (Q3) es el valor medio de la mitad superior de los datos.

Por ejemplo, aquí hay un conjunto de datos con 11 valores.

Mesa\(\PageIndex{1}\)

\(12\)	\(19\)	\(20\)	\(21\)	\(22\)	\(33\)	\(34\)	\(35\)	\(40\)	\(40\)	\(49\)
		Q1			Q2			Q3

• La mediana es 33.
• El primer cuartil es 20. Es la mediana de los números menores a 33.
• El tercer cuartil 40. Es la mediana de los números mayores a 33.

La diferencia entre los valores máximo y mínimo de un conjunto de datos es el rango. La diferencia entre Q3 y Q1 es el rango intercuartil (IQR). Debido a que la distancia entre Q1 y Q3 incluye las dos cuartas partes medias de la distribución, los valores entre esos dos cuartiles a veces se denominan la mitad media de los datos.

Cuanto más grande es el IQR, más extendido está la mitad media de los valores de los datos. Cuanto más pequeño es el IQR, más cerca están la mitad media de los valores de los datos. Es por ello que podemos utilizar el IQR como medida de propagación.

Se puede usar un resumen de cinco números para resumir una distribución. Incluye el mínimo, primer cuartil, mediana, tercer cuartil y máximo del conjunto de datos. Para el ejemplo anterior, el resumen de cinco números es 12, 20, 33, 40 y 49. Estos números están marcados con diamantes en la parcela de puntos.

Figura\(\PageIndex{4}\): Gráfica de puntos. Se indican los números del 10 al 50, en incrementos de 5. Hay diamantes indicados en 12, 20, 33, 40 y 49. Los datos son los siguientes: 12, 1 punto; 19, 1 punto; 20, 1 punto; 21, 1 punto; 22, 1 punto; 33, 1 punto; 34, 1 punto; 35, 1 punto; 40, 1 punto; 49, 2 puntos.

Diferentes conjuntos de datos pueden tener el mismo resumen de cinco números. Por ejemplo, aquí hay otro conjunto de datos con el mismo mínimo, máximo y cuartiles que el ejemplo anterior.

Figura\(\PageIndex{5}\): Gráfica de puntos. Se indican los números del 10 al 50, en incrementos de 5. Hay diamantes indicados en 12, 20, 33, 40 y 49. Los datos son los siguientes: 12, 1 punto; 14, 1 punto; 16, 1 punto; 18, 1 punto; 20, 1 punto; 24, 1 punto; 26, 1 punto; 28, 1 punto; 31, 1 punto; 33, 2 puntos; 36, 1 punto; 38, 1 punto; 39, 1 punto; 40, 1 punto; 44, 1 punto; 46, 1 punto; 48, 1 punto; 49, 1 punto punto.

Entradas en el glosario

Definición: Rango Intercuartil (IQR)

El rango intercuartílico es una forma de medir qué tan extendido está un conjunto de datos. A esto a veces lo llamamos el IQR. Para encontrar el rango intercuartil restamos el primer cuartil del tercer cuartil.

Por ejemplo, el IQR de este conjunto de datos es 20 porque\(50-30=20\).

Mesa\(\PageIndex{2}\)

\(22\)	\(29\)	\(30\)	\(31\)	\(32\)	\(43\)	\(44\)	\(45\)	\(50\)	\(50\)	\(59\)
		Q1			Q2			Q3

Definición: Mediana

La mediana es una forma de medir el centro de un conjunto de datos. Es el número medio cuando el conjunto de datos está listado en orden.

Para el conjunto de datos 7, 9, 12, 13, 14, la mediana es 12.

Para el conjunto de datos 3, 5, 6, 8, 11, 12, hay dos números en el medio. La mediana es el promedio de estos dos números. \(6+8=14\)y\(14\div 2=7\).

Definición: Cuartil

Los cuartiles son los números que dividen un conjunto de datos en cuatro secciones que cada una tiene el mismo número de valores.

Por ejemplo, en este conjunto de datos el primer cuartil es 30. El segundo cuartil es lo mismo que la mediana, que es 43. El tercer cuartil es 50.

Mesa\(\PageIndex{3}\)

\(22\)	\(29\)	\(30\)	\(31\)	\(32\)	\(43\)	\(44\)	\(45\)	\(50\)	\(50\)	\(59\)
		Q1			Q2			Q3

Definición: Rango

El rango es la distancia entre los valores más pequeños y mayores en un conjunto de datos. Por ejemplo, para el conjunto de datos 3, 5, 6, 8, 11, 12, el rango es 9, porque\(12-3=9\).

Practica

Ejercicio\(\PageIndex{4}\)

Supongamos que hay 20 números en un conjunto de datos y que todos son diferentes.

1. ¿Cuántos de los valores de este conjunto de datos se encuentran entre el primer cuartil y el tercer cuartil?
2. ¿Cuántos de los valores de este conjunto de datos se encuentran entre el primer cuartil y la mediana?

Ejercicio\(\PageIndex{5}\)

En un juego de palabras, 1 letra vale 1 punto. Esta gráfica de puntos muestra las puntuaciones de 20 palabras comunes.

Figura\(\PageIndex{6}\)

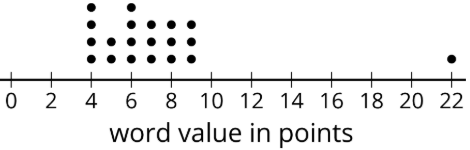
1. ¿Cuál es la puntuación media?
2. ¿Cuál es el primer cuartil (Q1)?
3. ¿Qué es el tercer cuartil (Q3)?
4. ¿Qué es el rango intercuartil (IQR)?

Ejercicio\(\PageIndex{6}\)

Mai y Priya jugaron cada uno 10 juegos de bolos y registraron los puntajes. La mediana de la puntuación de Mai fue de 120, y su IQR fue de 5. La mediana de puntuación de Priya fue de 118, y su IQR fue de 15. ¿Cuyos puntajes probablemente tuvieron menos variabilidad? Explica cómo sabes.

Ejercicio\(\PageIndex{7}\)

Aquí hay cinco parcelas de puntos que muestran las cantidades de tiempo que diez estudiantes de sexto grado en cinco países tardaron en llegar a la escuela. Haga coincidir cada gráfico de puntos con la mediana y el IQR apropiados.

Figura\(\PageIndex{7}\): Cinco parcelas de puntos para “tiempo de viaje en minutos” etiquetadas como “Estados Unidos”, “Canadá”, “Australia”, “Nueva Zelanda” y “Sudáfrica”. Cada gráfica de puntos tiene los números del 0 al 60, en incrementos de 10. También hay marcas de garrapatas a medio camino entre. Los datos aproximados para “Estados Unidos” son los siguientes: 2 minutos, 2 puntos; 7 minutos, 2 puntos; 8 minutos, 3 puntos; 11 minutos, 1 punto; 17 minutos, 1 punto; 20 minutos, 1 punto. Los datos aproximados para “Canadá” son los siguientes: 1 minuto, 1 punto; 2 minutos, 1 punto; 5 minutos, 2 puntos; 7 minutos, 2 puntos; 10 minutos, 1 punto; 15 minutos, 1 punto; 28 minutos, 1 punto; 30 minutos, 1 punto. Los datos aproximados para “Australia” son los siguientes: 5 minutos, 1 punto; 7 minutos, 1 punto; 9 minutos, 1 punto; 15 minutos, 2 puntos; 20 minutos, 3 puntos; 25 minutos, 1 punto; 45 minutos, 1 punto. Los datos aproximados para “Nueva Zelanda” son los siguientes: 3 minutos, 1 punto; 6 minutos, 1 punto; 7 minutos, 1 punto; 10 minutos, 2 puntos; 15 minutos, 3 puntos; 20 minutos, 1 punto; 24 minutos, 1 punto. Los datos aproximados para “Sudáfrica” son los siguientes: 5 minutos, 2 puntos; 10 minutos, 2 puntos; 15 minutos, 2 puntos; 30 minutos, 1 punto; 40 minutos, 1 punto; 45 minutos, 1 punto; 60 minutos, 1 punto.

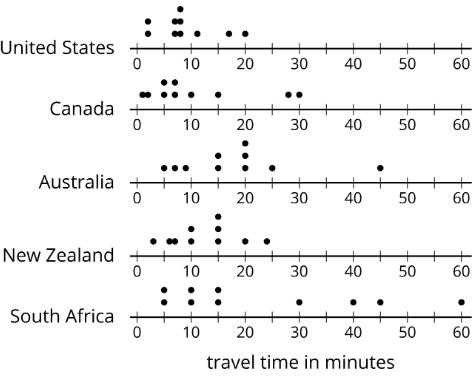
1. Mediana: 17,5, IQR: 11
2. Mediana: 15, IQR: 30
3. Mediana: 8, IQR: 4
4. Mediana: 7, IQR: 10
5. Mediana: 12.5, IQR: 8

Ejercicio\(\PageIndex{8}\)

Dibuja y etiqueta un par de ejes apropiados y trazar los puntos. \(A=(10,50), B=(30,25), C=(0,30), D=(20,35)\)

(De la Unidad 7.3.2)

Ejercicio\(\PageIndex{9}\)

Hay 20 centavos en un frasco. Si el 16% de las monedas en el frasco son centavos, ¿cuántas monedas hay en el frasco?

(De la Unidad 6.2.2)