1.7: Funciones exponenciales
- Page ID
- 110562
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Considera estas dos empresas:
- La empresa A cuenta con 100 tiendas, y se expande abriendo 50 nuevas tiendas al año
- La empresa B cuenta con 100 tiendas, y se expande al aumentar el número de tiendas en un 50% de su total cada año.
La empresa A está exhibiendo un crecimiento lineal. En el crecimiento lineal, tenemos una tasa constante de cambio, un número constante que la salida aumentó por cada aumento en la entrada. Para la empresa A, el número de tiendas nuevas por año es el mismo cada año.
La compañía B es diferente: tenemos una tasa de cambio porcentual en lugar de un número constante de tiendas/año como nuestra tasa de cambio. Para ver la significancia de esta diferencia compara un incremento del 50% cuando hay 100 tiendas a un incremento del 50% cuando hay 1000 tiendas:
- 100 tiendas, un incremento del 50% son 50 tiendas en ese año.
- 1000 tiendas, un incremento del 50% son 500 tiendas en ese año.
Calculando el número de tiendas después de varios años, podemos ver claramente la diferencia en los resultados.
| Años | Empresa A | Empresa B |
| 2 | 200 | 225 |
| 4 | 300 | 506 |
| 6 | 400 | 1139 |
| 8 | 500 | 2563 |
| 10 | 600 | 5767 |
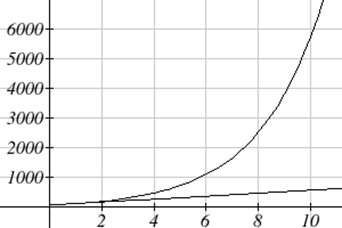
Este porcentaje de crecimiento se puede modelar con una función exponencial.
Una función de crecimiento o decaimiento exponencial es una función que crece o se contrae a una tasa de crecimiento porcentual constante. La ecuación se puede escribir en la forma\[ f(x)=a(1+r)^x\nonumber \] o\[ f(x)=ab^x\nonumber \] donde\( b=1+r \).
Dónde
- \(a\)es el valor inicial o inicial de la función,
- \(r\)es el porcentaje de crecimiento o tasa de decaimiento, escrito como decimal,
- \(b\)es el factor de crecimiento o multiplicador de crecimiento. Dado que los poderes de los números negativos se comportan de manera extraña, limitamos\(b\) a valores positivos.
La población de la India era de 1.14 mil millones en el año 2008 y está creciendo alrededor de 1.34% cada año. Escriba una función exponencial para la población de la India, y utilícela para predecir la población en 2020.
Solución
Usando 2008 como nuestra hora de inicio (\(t = 0\)), nuestra población inicial será de 1.14 mil millones. Dado que la tasa de crecimiento porcentual fue de 1.34%, nuestro valor para\(r\) es de 0.0134.
Usando la fórmula básica para el crecimiento exponencial\(f(x)=a(1+r)^x\) podemos escribir la fórmula,\[f(t)=1.14(1+0.0134)^{t}\nonumber \]
Para estimar la población en 2020, evaluamos la función en\(t = 12\), ya que 2020 es 12 años después de 2008:\[f(t)=1.14(1+0.0134)^{12}\approx 1.337 \text{ billion people in 2020.}\nonumber \]
Un certificado de depósito (CD) es un tipo de cuenta de ahorro que ofrecen los bancos, que suelen ofrecer una tasa de interés más alta a cambio de un período de tiempo fijo que dejará su dinero invertido. Si un banco ofrece un CD de 24 meses con una tasa de interés anual de 1.2% compuesta mensualmente, ¿a cuánto crecerá una inversión de $1000 a lo largo de esos 24 meses?
Solución
Primero, debemos notar que la tasa de interés es una tasa anual, pero se compone mensualmente, es decir, el interés se calcula y se agrega a la cuenta mensualmente. Para encontrar la tasa de interés mensual, dividimos la tasa anual de 1.2% por 12 ya que hay 12 meses en un año: 1.2% /12 = 0.1%. Cada mes ganaremos 0.1% de interés. A partir de esto, podemos establecer una función exponencial, con nuestro monto inicial de $1000 y una tasa de crecimiento de\( r = 0.001\), y nuestro input\(m\) medido en meses:\[f(m)=1000\left(1+\frac{0.012}{12}\right)^m=1000(1.001)^{m}\nonumber \]
Después de 24 meses, la cuenta habrá crecido hasta\( f(24)=1000(1.001)^{24}\approx \$1024.28 \).
El bismuto-210 es un isótopo que se descompone radiactivamente en aproximadamente 13% cada día, lo que significa que 13% del resto de bismuto-210 se transforma en otro átomo (polonio-210 en este caso) cada día. Si comienzas con 100 mg de bismuto-210, ¿cuánto queda después de una semana?
Solución
Con la desintegración radiactiva, en lugar de que la cantidad aumente a una tasa porcentual, la cantidad está disminuyendo a una tasa porcentual. Nuestra cantidad inicial es\(a = 100\) mg, y nuestra tasa de crecimiento será negativa 13%, ya que estamos disminuyendo:\( r = -0.13\). Esto da la ecuación\[ Q(d)=100(1-0.13)^d=100(0.87)^d.\nonumber \] Esto también se puede explicar reconociendo que si el 13% decae, entonces queda 87%.
Después de una semana, 7 días, la cantidad restante sería\( Q(7)=100(0.87)^7=37.73 \) mg de restos de bismuto-210.
\(T(q)\)representa el número total de contratos de teléfonos inteligentes Android, en miles, mantenidos por cierta región de tiendas de Verizon medidos trimestralmente desde el 1 de enero de 2010. Interpretar todas las partes de la ecuación\( T(2)=86(1.64)^2=231.3056 \).
Solución
Interpretando esto desde la forma exponencial básica, sabemos que 86 es nuestro valor inicial. Esto significa que el 1 de enero de 2010 esta región tenía 86 mil contratos de teléfonos inteligentes Android. Ya que\(b = 1 + r = 1.64\), sabemos que cada trimestre el número de contratos de teléfonos inteligentes crece 64%. \(T(2) = 231.3056\)significa que en el segundo trimestre (o al final del segundo trimestre) hubo aproximadamente 231,305 contratos de teléfonos inteligentes Android.
Al trabajar con exponenciales, hay una constante especial de la que debemos hablar. Surge cuando hablamos de cosas que crecen continuamente, como la composición continua, o fenómenos naturales como la desintegración radiactiva que ocurren continuamente.
\[e\approx 2.718282\nonumber \]
Debido a que a menudo\(e\) se usa como base de un exponencial, la mayoría de las calculadoras científicas y gráficas tienen un botón que puede calcular potencias de\(e\), generalmente etiquetadas\(e^x\). Algunos programas informáticos en cambio definen una función\(exp(x)\), donde exp (x) =\(e^x\). Dado que el cálculo estudia el cambio continuo, casi siempre utilizaremos la forma\(e\) basada de ecuaciones exponenciales en este curso.
El crecimiento continuo se puede calcular usando la fórmula\[f(x)=ae^{rx}\nonumber \] donde
- \(a\)es la cantidad inicial,
- \(r\)es la tasa de crecimiento continuo.
El radón-222 decae a una tasa continua de 17.3% por día. ¿Cuánto decaerán 100 mg de Radón-222 en 3 días?
Solución
Dado que se nos da una tasa de decaimiento continuo, utilizamos la fórmula de crecimiento continuo. Dado que la sustancia está en descomposición, sabemos que la tasa de crecimiento será negativa:\(r = -0.173\), se mantendrán\( f(3)=100e^{-0.173(3)}\approx 59.512 \) mg de Radón-222.
Gráficas de Funciones Exponenciales
Gráficamente, en la función\( f(x)=ab^x \).
- \(a\)es la intercepción vertical de la gráfica.
- \(b\)determina la velocidad a la que crece la gráfica:
- la función aumentará si\(b \gt 1\),
- la función disminuirá si\(0 \lt b \lt 1\).
- La gráfica tendrá una asíntota horizontal en\(y = 0\).
- La gráfica será cóncava hacia arriba si\(a \gt 0\); cóncava hacia abajo si\(a \lt 0\).
- El dominio de la función son todos los números reales.
- El rango de la función es\( (0,\infty) \).
Al esbozar la gráfica de una función exponencial, puede ser útil recordar que la gráfica pasará por los puntos\((0, a)\) y\((1, ab)\).
El valor\(b\) determinará el comportamiento a largo plazo de la función:
- Si\(b \gt 1\), como\( x\to\infty \),\( f(x)\to\infty \), y como\( x\to -\infty \),\( f(x)\to 0 \).
- Si\(0 \lt b \lt 1\), como\( x\to\infty \),\( f(x)\to 0 \), y como\( x\to -\infty \),\( f(x)\to \infty \).
Esbozar un gráfico de\( f(x)=4\left(\frac{1}{3}\right)^x \)
Solución
Esta gráfica tendrá una intercepción vertical en (0,4), y pasará por el punto\( \left(1,\frac{4}{3} \right) \). Ya que\(b \lt 1\), la gráfica estará disminuyendo hacia cero. Ya que\(a \gt 0\), la gráfica será cóncava hacia arriba.
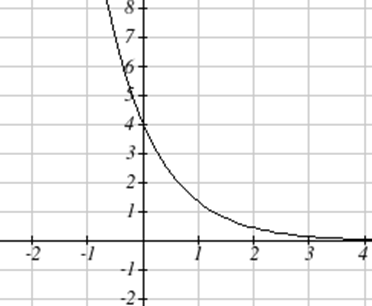
También podemos ver en la gráfica el comportamiento a largo plazo: as\( x\to\infty \),\( f(x)\to 0 \), y as\( x\to -\infty \),\( f(x)\to \infty \).
Para tener una mejor idea del efecto de\(a\) y\(b\) sobre la gráfica, examine los conjuntos de gráficos a continuación. El primer conjunto muestra diversas gráficas, donde\(a\) sigue siendo el mismo y solo cambiamos el valor por\(b\). Observe que cuanto más cerca\(b\) esté el valor de 1, menos empinada será la gráfica.
En el siguiente conjunto de gráficas,\(a\) se altera y nuestro valor para\(b\) sigue siendo el mismo.
Observe que cambiando el valor de a cambia la intercepción vertical. Ya que\(a\) se está multiplicando el\(b^x\) término,\(a\) actúa como factor de estiramiento vertical, no como un desplazamiento. Observe también que el comportamiento a largo plazo para todas estas funciones es el mismo porque el factor de crecimiento no cambió y ninguno de estos\(a\) valores introdujo un giro vertical.
Pruébalo tú mismo usando este applet:
Coincide cada ecuación con su gráfica.
- \( f(x)=2(1.3)^x \)
- \( g(x)=2(1.8)^x \)
- \( h(x)=4(1.3)^x \)
- \( k(x)=4(0.7)^x \)
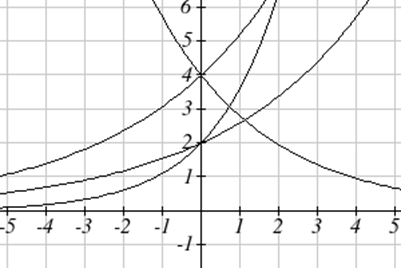
Solución
La gráfica de\(k(x)\) es la más fácil de identificar, ya que es la única ecuación con un factor de crecimiento menor a uno, lo que producirá una gráfica decreciente. La gráfica de se\(h(x)\) puede identificar como la única función exponencial creciente con una intercepción vertical en (0,4). Las gráficas de\(f(x)\) y\(g(x)\) ambas tienen una intercepción vertical en (0,2), pero como\(g(x)\) tiene un factor de crecimiento mayor, podemos identificarla como la gráfica que aumenta más rápido.


