13.1: Euler Tours y Senderos

Última actualización
Guardar como PDF

Page ID: 114429

Joy Morris
University of Lethbridge

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Para introducir estos conceptos, necesitamos conocer algunos tipos especiales de paseos.

Definición: Tipos Especiales de Obras

Una caminata se cierra si comienza y termina con el mismo vértice.
Un sendero es un paseo en el que no aparecen dos vértices consecutivamente (en ningún orden) más de una vez. (Es decir, no se usa ningún borde más de una vez).
Un recorrido es un sendero cerrado.
Un sendero de Euler es un sendero en el que cada par de vértices adyacentes aparecen consecutivamente. (Es decir, cada borde se usa exactamente una vez).
Un recorrido por Euler es un sendero cerrado de Euler.

Recordemos el ejemplo histórico de los puentes de Königsberg. El problema de encontrar una ruta que cruce cada puente exactamente una vez, equivale a encontrar un sendero de Euler en la gráfica correspondiente. Si queremos que la ruta comience y termine en el mismo lugar (por ejemplo, la casa de alguien), entonces el problema equivale a encontrar un recorrido de Euler en la gráfica correspondiente.

Los recorridos y senderos de Euler son herramientas importantes para planificar rutas para tareas como recolección de basura, barrido de calles y búsquedas.

Ejemplo$\PageIndex{1}$

En la gráfica

$clipboard_e3cd58b54ec3a63d6d80d1c8521bd96d7.png$

$(i, b, c, h, i, d, e, f, g, d, a, g, j, a)$es un sendero de Euler. En la gráfica

$clipboard_e02e0cfb483c7c7c0bc2b01885cf4a1b8.png$

$(a, e, f, b, g, f, c, d, h, c, g, d, f, a)$es una gira de Euler.

Aquí está el método de Euler para encontrar tours de Euler. Lo declararemos para multígrafos, ya que eso hace que el resultado correspondiente sobre los senderos de Euler sea un corolario muy fácil.

Teorema$\PageIndex{1}$

Una gráfica conectada (o multígrafo, con o sin bucles) tiene un recorrido de Euler si y solo si cada vértice de la gráfica tiene valencia par.

Prueba

Como la afirmación es si y sólo si, debemos probar ambas implicaciones.

\ ((⇒) Supongamos que tenemos un multígrafo (posiblemente con bucles) que tiene una gira de Euler,

\[(u_1, u_2, . . . , u_{e+1} = u_1),\]

donde$e = |E|$. Dejar$u$ ser un vértice arbitrario del multígrafo. Cada vez$u$ que aparece en el recorrido,$u$ se utilizan exactamente dos de los bordes incidentes con: si$u = u_j$, entonces los bordes utilizados son$u_{j−1}u_j$ y$u_ju_{j−1}$ a menos$j = 1$ o$j = e + 1$ en cuyo caso$u = u_1 = u_{e+1}$ y los bordes son$u_eu$ y$uu_2$ (y consideramos esto como uno aparición de u en el recorrido). Por lo tanto, si$u$ aparece$k$ tiempos en el recorrido, entonces ya que por la definición de un recorrido de Euler todos los bordes incidentes con se$u$ utilizan exactamente una vez, concluimos que$u$ debe tener valencia$2k$. Ya que$u$ era un vértice arbitrario del multígrafo y$k$ (el número de veces que$u$ aparece en el recorrido) debe ser un número entero, esto demuestra que la valencia de cada vértice debe ser pareja.

$(⇐)$Supongamos que tenemos un multígrafo conectado en el que la valencia de cada vértice es pareja. Considere el siguiente algoritmo (que será la primera etapa de nuestro algoritmo final):

Hacer$u$ (algún vértice arbitrario) nuestro vértice activo, con una lista$L$ de todos los bordes de$E$. Hacer$u$ el primer vértice en una nueva secuencia$C$ de vértices. Repita el siguiente paso tantas veces como sea posible:

Llamar al vértice activo$v$. Elija cualquier borde$vx$ en el$L$ que sea incidente con$v$. Agrega$x$ (el otro vértice final de este borde) al final de$C$, y haz$x$ el nuevo vértice activo. Quitar$vx$ de$L$.

Afirmamos que cuando este algoritmo termine, la secuencia$C$ será un recorrido (aunque no necesariamente un recorrido de Euler) en el multígrafo. Por construcción,$C$ es un paseo, y$C$ no se puede utilizar ningún borde más de una vez ya que cada borde aparece en una$L$ sola vez y se retira de$L$ una vez que se ha utilizado, por lo que$C$ es un sendero. Tenemos que demostrar que la caminata$C$ está cerrada.

La única forma en que el algoritmo puede terminar es si no$L$ contiene ningún borde que sea incidente con el vértice activo. Hacia una contradicción, supongamos que esto sucede en un momento en que el vértice activo es$y \neq u$. Ahora,$y$ tiene valencia$2r$ en el multígrafo para algún entero$r$, así que hubo$2r$ bordes en los$L$ que fueron incidentes con$y$ cuando iniciamos el algoritmo. Ya que$y \neq u$, cada vez que$y$ aparece en$C$ antes de esta aparición, eliminamos$2$ los bordes incidentes con$y$ de$L$ (uno en el paso cuando hicimos$y$ el vértice activo, y uno en el siguiente paso). Además, eliminamos un incidente de borde adicional con$y$ de$L$ en el paso final, cuando volvimos a hacer$y$ el vértice activo. Por lo tanto, si hay apariciones$t$ previas de$y$ en$C$, hemos eliminado$2t + 1$ bordes incidentes con$y$ de$L$. Dado que$2r$ es par y$2t+ 1$ es impar, aún debe haber al menos un incidente de borde con el$y$ que esté adentro$L$, contradiciendo el hecho de que el algoritmo terminó. Esta contradicción muestra que, cuando el algoritmo termina, el vértice activo debe ser$u$, por lo que la secuencia$C$ es un paseo cerrado. Ya que$C$ es un sendero, vemos que$C$ debe ser un recorrido.

Si el recorrido no$C$ es un recorrido de Euler, deja$y$ ser el primer vértice que aparece en$C$ para el que queda un borde incidente en$L$. Repita el algoritmo anterior comenzando por$y$ ser el vértice activo, y con$L$ comenzar en su estado actual (no todos$E$). El resultado será una gira que comienza y termina en y que usa solo bordes que no estaban en$C$. Inserte este tour de la$C$ siguiente manera: si$C = (u = u_1 . . . , y = u_i , . . . , u_k = u)$ y el nuevo tour es$(y = v_1, . . . , v_j = y)$, entonces el resultado de insertar el nuevo tour en$C$ será

\[(u = u_1, . . . , y = u_i = v_1, v_2, . . . , v_j = y = u_i , u_{i+1}, . . . , u_k = u).\]

Reemplazar$C$ por este recorrido extendido.

Repetir el proceso descrito en el párrafo anterior tantas veces como sea posible (esta es la segunda y última etapa de nuestro algoritmo final). Ya que$E$ es finito y el multígrafo está conectado, tarde o temprano todos los bordes de$L$ deben estar agotados. En este punto, debemos tener un recorrido por Euler.

Ejemplo$\PageIndex{2}$

Utilice el algoritmo descrito en la prueba del resultado anterior, para encontrar un recorrido de Euler en la siguiente gráfica.

$clipboard_e84ae166bb6b63fa2823d3add61f6d47e.png$

Solución

Comencemos el algoritmo en$a$. Como$E = L$ es un conjunto grande, no enumeraremos los elementos restantes cada vez que elegimos un nuevo vértice activo en las primeras etapas. Un método fácil para hacer un seguimiento de los bordes aún adentro$L$ es colorear los bordes que ya no están$L$ (los bordes que usamos) con un color diferente a medida que avanzamos.

Hay muchos resultados posibles diferentes para el algoritmo ya que a menudo hay muchas opciones aceptables para el siguiente vértice activo. Un conjunto inicial de opciones podría ser

$C = (a, b, f, e, a, f, g, a).$

La primera etapa del algoritmo termina en este punto ya que se$a$ han utilizado los cuatro bordes incidentes con. En este punto, tenemos

$L = \{bg, bh, cd, cf, cg, ch, df, dg, dh, gh\}.$

El primer vértice en$C$ que es incidente con un borde adentro$L$ es$b$. Ejecutamos la primera etapa del algoritmo nuevamente con$b$ como el vértice activo inicial y esta lista para$L$. Nuevamente, hay muchos resultados posibles; uno es$(b, g, h, b)$.

Insertamos$(b, g, h, b)$ en$C$, obteniendo un nuevo$C = (a, b, g, h, b, f, e, a, f, g, a)$. En este punto, tenemos

$L = \{cd, cf, cg, ch, df, dg, dh\}.$

Ahora$g$ es el primer vértice en$C$ que es incidente con un borde adentro$L$. Ejecutamos la primera etapa del algoritmo nuevamente con$g$ como el vértice activo inicial y el actual$L$. Un posible resultado es$(g, c, f, d, g)$.

Insertando esto en$C$ produce un nuevo

$C = (a, b, g, c, f, d, g, h, b, f, e, a, f, g, a).$

En este punto, tenemos$L = \{cd, ch, dh\}$. El primer vértice en$C$ que es incidente con un borde adentro$L$ es$c$. Ejecutamos la primera etapa del algoritmo una última vez con$c$ como vértice activo inicial y$L = \{cd, ch, dh\}$. Esta vez sólo hay dos posibles resultados:$(c, d, h, c)$ o$(c, h, d, c)$. Nosotros elegimos$(c, d, h, c)$.

Insertando esto en$C$ los rendimientos de nuestro tour de Euler:

$C = (a, b, g, c, d, h, c, f, d, g, h, b, f, e, a, f, g, a).$

Corolario$\PageIndex{1}$

Una gráfica conectada (o multígrafo, con o sin bucles) tiene un rastro de Euler si y solo si a lo sumo dos vértices tienen valencia impar.

Prueba

Supongamos que tenemos una gráfica conectada (o multígrafo, con o sin bucles),$G$. Ya que la afirmación es si y sólo si, hay dos implicaciones que probar.

$(⇒)$Supongamos que$G$ tiene un rastro de Euler. Si el sendero está cerrado entonces es un recorrido, y por el Teorema 13.1.1, no hay vértices de valencia impar. Si el sendero no está cerrado, digamos que es un$u − v$ paseo. Agregar un borde entre$u$ y$v$ a$G$, crear una nueva gráfica$G^∗$ (tenga en cuenta que$G^∗$ puede ser un multígrafo si ya$uv$ era un borde de$G$, aunque no$G$ fuera un multígrafo), y agregue$u$ al final del sendero de Euler en$G$, para crear un recorrido por Euler en$G^∗$. Por Teorema 13.1.1, el hecho de que$G^∗$ tenga una gira de Euler significa que cada vértice de$G^∗$ tiene incluso valencia. Ahora bien, los vértices de$G$ todos tienen la misma valencia en$G^∗$ que tienen adentro$G$, con la excepción de que las valencias de$u$ y$v$ son una$G^∗$ mayor adentro que en$G$. Por lo tanto, en este caso hay exactamente dos vértices de valencia impar en$G$; es decir,$u$ y$v$.

$(⇐)$Ahora suponemos que$G$ tiene como máximo$2$ vértices de valencia impar. Por Corolario 11.3.1 (el corolario del lema de apretón de manos de Euler), si hay como máximo dos vértices de valencia impar, entonces hay uno$0$ o$2$ vértices de valencia impar. Consideramos estos dos casos.

Si hay$0$ vértices de valencia impar, entonces por el Teorema 13.1.1,$G$ tiene un recorrido de Euler.

Si hay dos vértices de valencia impar, digamos$u$ y$v$, agregar un borde entre$u$ y$v$ a$G$, creando una nueva gráfica$G^∗$ (nótese que$G^∗$ puede ser un multígrafo si ya$uv$ era un borde de$G$, aunque no$G$ fuera un multígrafo). Ahora en$G^∗$ cada vértice tiene incluso valencia, así$G^∗$ tiene una gira de Euler. De hecho, una mirada cuidadosa al algoritmo dado en la prueba del Teorema 13.1.1 muestra que podemos elegir$u$ y$v$ (en ese orden) ser los dos primeros vértices en este recorrido de Euler, de manera que$uv$ (el borde que está en$G^∗$ pero no$G$) es el primer borde utilizado en el recorrido. Ahora bien, si eliminamos$u$ del inicio de esta gira de Euler, el resultado es un sendero de Euler en$G$ que comienza en$v$ y termina en$u$.

Ejercicio$\PageIndex{1}$

Para cada una de las siguientes gráficas, ¿hay un recorrido por Euler? ¿Hay un rastro de Euler? Si alguno existe, encuentra uno; si no, explica por qué no.

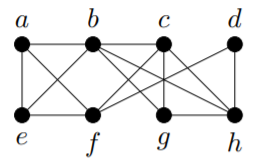
1) $clipboard_e04a984a60fcc07768fbca28bc192555f.png$

2) $clipboard_e18c4f00db6996c9494e395719a293956.png$

3) $clipboard_e1a2e43eefd75f4509db7865025f31d16.png$

4) Si es posible, dibuja una gráfica que tenga un número par de vértices y un número impar de aristas, que también tenga un recorrido por Euler. Si eso no es posible, explique por qué no existe tal gráfica.

5) ¿Qué gráficas completas tienen un recorrido por Euler? De las gráficas completas que no tienen un recorrido por Euler, ¿cuáles de ellas tienen un rastro de Euler?

Ejercicio$\PageIndex{2}$

Falta el gato de Sylvia. Ella quiere buscarlo en todas las calles cercanas, pero está cansada y no quiere caminar más lejos de lo que debe. Encuentra una ruta eficiente para que Sylvia la lleve por su vecindario para que comience y termine en su casa y camine por cada calle exactamente una vez. La ubicación de la casa de Sylvia está marcada con un símbolo en forma de casa ( $clipboard_e0c4a6e4818032f2055d6be635c0cc852.png$ ).

$clipboard_e48652834b9e6ce5d6af5703579b98f29.png$

Search

Text Color

Text Size

Margin Size

Font Type