13.2: Caminos y Ciclos Hamilton

Última actualización
Guardar como PDF

Page ID: 114437

Joy Morris
University of Lethbridge

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

A veces, en lugar de viajar a lo largo de cada conexión en una red, nuestro objetivo es simplemente visitar cada nodo de la red. Esto se relaciona con una estructura diferente en la gráfica correspondiente.

Definición: Hamilton Cycle

Un ciclo de Hamilton es un ciclo que visita cada vértice de la gráfica. Un camino de Hamilton es un camino que visita cada vértice de la gráfica.

Las definiciones de trayectoria y ciclo aseguran que los vértices no se repitan. Los caminos y los ciclos de Hamilton son herramientas importantes para planificar rutas para tareas como la entrega de paquetes, donde el punto importante no son las rutas tomadas, sino los lugares que se han visitado.

En 1857, William Rowan Hamilton presentó por primera vez un juego que llamó el “juego icosiano”. Implicaba trazar los bordes de un dodecaedro de tal manera que visitara cada esquina precisamente una vez. De hecho, dos años antes el reverendo Thomas Kirkman había enviado una ponencia a la Royal Society de Londres, en la que planteaba el problema de encontrar lo que llamó polígonos cerrados en poliedros; un polígono cerrado que definió como un circuito de aristas que pasa por cada vértice una sola vez. Así, Kirkman había planteado un problema más general antes de Hamilton (e hizo algunos avances para resolverlo); sin embargo, es Hamilton para quien ahora se nombra a estas estructuras. Como veremos más adelante al estudiar Steiner Triple Systems en teoría del diseño, Kirkman era un matemático talentoso que parece haber sido singularmente desafortunado en términos de recibir el crédito adecuado por sus logros. Como su título indica, Kirkman era un ministro que perseguía las matemáticas por un lado, como una pasión personal.

Hamilton logró convencer a la compañía de John Jacques e hijos, que eran fabricantes de juguetes (incluidos juegos de ajedrez de alta calidad) para producir y comercializar el “juego icosiano”. Fue producido bajo el nombre Around the World, y se vendió en dos formas: una tabla plana, o un dodecaedro real. En ambos casos, se colocaron clavos en las esquinas del dodecaedro representando ciudades, y el juego se jugó envolviendo una cuerda alrededor de las uñas, viajó solo por bordes, visitando cada uña una vez, y terminando en el punto de partida. Desafortunadamente, el juego no fue un éxito financiero. No es muy difícil y se vuelve poco interesante una vez resuelto.

Los bordes gruesos forman un ciclo de Hamilton en la gráfica del dodecaedro:

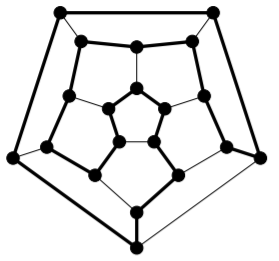
$clipboard_ea090fabf325d0065e6eb02dd339a1509.png$

No todas las gráficas conectadas tienen un ciclo Hamilton; de hecho, no todas las gráficas conectadas tienen un camino Hamilton.

Figura$\PageIndex{1}$: Una gráfica con un camino de Hamilton pero sin ciclo Hamilton. (Copyright; autor vía fuente)

Figura$\PageIndex{2}$: Una gráfica sin trayectoria Hamilton. (Copyright; autor vía fuente)

Desafortunadamente, en contraste con el resultado de Euler sobre recorridos y senderos de Euler (dados en el Teorema 13.1.1 y Corolario 13.1.1), no se conoce ninguna caracterización que nos permita determinar rápidamente si una gráfica arbitraria tiene o no un ciclo (o camino) de Hamilton. Este es un problema duro en general. Sabemos de algunas condiciones necesarias (cualquier gráfica que no cumpla con estas condiciones no puede tener un ciclo Hamilton) y algunas condiciones suficientes (cualquier gráfica que cumpla con estas debe tener un ciclo Hamilton). Sin embargo, muchas gráficas no cumplen ninguna de estas condiciones. También hay algunas condiciones que son necesarias o suficientes para la existencia de un camino Hamilton.

Aquí hay una condición necesaria para que una gráfica tenga un ciclo Hamilton.

Teorema$\PageIndex{1}$

Si$G$ es una gráfica con un ciclo Hamilton, entonces para cada$S ⊂ V$ con$S \neq ∅$,$V$, la gráfica$G \setminus S$ tiene como máximo componentes$|S|$ conectados.

Prueba

Let$C$ Be a Hamilton cycle in$G$. Arreglar un subconjunto arbitrario apropiado y no vacío$S$ de$V$.

Uno a la vez, eliminar los vértices de$S$ desde$C$. Después de eliminar el primer vértice, el resultado sigue conectado, pero se ha convertido en un camino. Cuando se elimina cualquiera de$|S| − 1$ los vértices subsiguientes, se rompe alguna ruta en dos caminos más cortos (aumentando en uno el número de componentes conectados) o elimina un vértice al final de alguna ruta (dejando el número de componentes conectados sin cambios, o reduciéndolo en uno si este componente era un $P_0$). Así$C \setminus S$ tiene como máximo componentes$1 + (|S| − 1) = |S|$ conectados.

Observe que si dos vértices$u$ y$v$ están en el mismo componente conectado de$C \setminus S$, entonces también estarán en el mismo componente conectado de$G \setminus S$. Esto se debe a que agregar bordes solo puede conectar las cosas de manera más completa, lo que reduce el número de componentes conectados. De manera más formal, si hay un$u − v$ paseo adentro$C$, entonces cualquier par de vértices consecutivos en ese paseo es adyacente en$C$ así que también es adyacente adentro$G$. Por lo tanto el mismo paseo es un$u − v$ paseo por dentro$G$. Esto nos dice que el número de componentes conectados de$G \setminus S$ es como máximo el número de componentes conectados de$C \setminus S$, que hemos demostrado ser como máximo$|S|$.

Ejemplo$\PageIndex{1}$

Cuando una no-hoja se elimina de una ruta de longitud al menos$2$, la eliminación de este vértice único deja dos componentes conectados. Entonces ningún camino de longitud al menos$2$ contiene un ciclo de Hamilton.

Aquí hay una gráfica en la que la inexistencia de un ciclo de Hamilton podría ser menos obvia sin el Teorema 13.2.1. La eliminación de los tres vértices blancos deja cuatro componentes conectados.

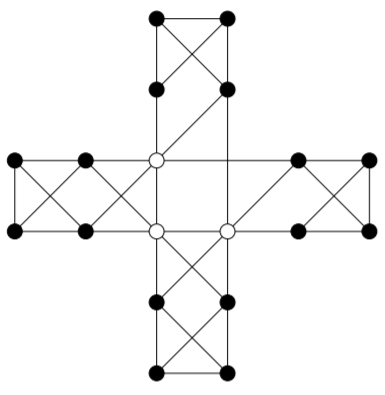
$clipboard_e1ba37eabce3d720c11d0aa90e4522f8a.png$

Como cabría esperar, si todos los vértices de una gráfica tienen una valencia suficientemente alta, siempre será posible encontrar un ciclo de Hamilton en la gráfica. (De hecho, generalmente la gráfica tendrá muchos ciclos Hamilton diferentes). Antes de que podamos formalizar esta idea, es útil tener una pieza adicional de notación.

Definición: Mínima y Máxima Valencia

La valencia mínima de una gráfica$G$ es

\[\min_{v∈V}d(v).\]

La valencia máxima de una gráfica$G$ es

\[\max_{v∈V}d(v).\]

Notación

Usamos$δ$ para denotar la valencia mínima de una gráfica, y$∆$ para denotar su valencia máxima. Si necesitamos aclarar la gráfica involucrada, usamos$δ(G)$ o$∆(G)$.

Teorema$\PageIndex{2}$: (Dirac, $1952$)

Si$G$ es una gráfica con vértice establecido$V$ tal que$|V| ≥ 3$ y$δ(G) ≥ \dfrac{|V|}{2}$, después$G$ tiene un ciclo Hamilton.

Prueba

Hacia una contradicción, supongamos que$G$ es una gráfica con vértice establecido$V$, eso$|V| = n ≥ 3$, y aquello$δ(G) ≥ \dfrac{n}{2}$, pero no$G$ tiene ciclo Hamilton.

Repita lo siguiente tantas veces como sea posible: si hay un borde al que se pueda agregar$G$ sin crear un ciclo de Hamilton en la gráfica resultante, agregue ese borde a$G$. Cuando esto se haya hecho tantas veces como sea posible, llame a la gráfica resultante$H$. La gráfica$H$ tiene el mismo conjunto de vértices$V$, y como hemos agregado bordes no hemos disminuido la valencia de ningún vértice, así que tenemos$δ(H) ≥ \dfrac{n}{2}$. Ahora,$H$ todavía no tiene ciclo Hamilton, pero agregar cualquier borde para$H$ dar una gráfica que sí tiene un ciclo Hamilton.

Dado que las gráficas completas en al menos tres vértices siempre tienen ciclos Hamilton (ver Ejercicio 13.2.1 (1)), debemos tener$H \ncong K_n$, por lo que hay al menos dos vértices de$H$, digamos$u$ y$v$, que no son adyacentes. Por nuestra construcción de$H$ desde$G$, agregar el borde$uv$ a$H$ resultaría en un ciclo Hamilton, y este ciclo Hamilton debe usar el borde$uv$ (de lo contrario sería un ciclo Hamilton en$H$, pero no$H$ tiene ciclo Hamilton). Así, la porción del ciclo de Hamilton que se encuentra en$H$ forma un camino de Hamilton desde$u$ hasta$v$. Escribe este camino de Hamilton como

\[(u = u_1, u_2, . . . , u_n = v)\]

Definir los conjuntos

\[S = \{ui | u ∼ u_{i+1}\} \text{ and } T = {u_i | v ∼ u_i}.\]

Es decir,$S$ es el conjunto de vértices que aparecen inmediatamente ante un vecino de$u$ en el camino de Hamilton, mientras que$T$ es el conjunto de vértices en el camino de Hamilton que son vecinos de$v$. Observe que$v = u_n \notin S$ ya$u_{n+1}$ no está definido, y$v = u_n \notin T$ ya que nuestras gráficas son simples (así que no tienen bucles). Así,$u_n \notin S ∪ T$, entonces$|S ∪ T| < n$.

Hacia una contradicción, supongamos que para algunos$i$,$u_i ∈ S ∩ T$. Entonces por las definiciones de$S$ y$T$, tenemos$u ∼ u_{i+1}$ y$v ∼ u_i$, entonces:

$clipboard_e00e1ef1b96a041a4e0c76f928aed1713.png$

es un ciclo Hamilton en$H$, lo que contradice nuestra construcción de$H$ como una gráfica que no tiene ciclo Hamilton. Esta contradicción sirve para demostrarlo$|S ∩ T| = ∅$.

Ahora tenemos

\[d_H(u) + d_H(v) = |S| + |T| = |S ∪ T| + |S ∩ T|\]

(la última igualdad viene de Inclusión-Exclusión). Pero lo hemos visto$|S ∪ T| < n$ y$|S ∩ T| = 0$, así que esto da

\[d_H(u) + d_H(v) < n.\]

Esto contradice$δ(H) ≥ \dfrac{n}{2}$, ya que

\[d_H(u), d_H(v) ≥ δ(H)\]

Esta contradicción sirve para demostrar que ninguna gráfica$G$ con vértice establecido$V$ tal que$|V| ≥ 3$ y$δ(G) ≥ \dfrac{|V|}{2}$ pueda dejar de tener un ciclo de Hamilton.

De hecho, la afirmación del teorema de Dirac fue mejorada por Bondy y Chvatal en 1974. Comenzaron observando que la prueba dada anteriormente para el Teorema de Dirac en realidad demuestra el siguiente resultado.

Lema$\PageIndex{1}$

Supongamos que$G$ es una gráfica en$n$ vértices,$u$ y$v$ son vértices no adyacentes de$G$, y$d(u) + d(v) ≥ n$. Entonces$G$ tiene un ciclo Hamilton si y sólo si la gráfica obtenida sumando el borde$uv$ a$G$ tiene un ciclo Hamilton.

Con esto en mente, hicieron la siguiente definición.

Definición: Cierre

Dejar$G$ ser una gráfica sobre$n$ vértices. El cierre de$G$ es la gráfica obtenida uniendo repetidamente pares de vértices no adyacentes$u$ y$v$ para los cuales$d(u) + d(v) ≥ n$, hasta que no exista tal par.

Antes de poder trabajar con esta definición, tenían que demostrar que el cierre de una gráfica está bien definido. En otras palabras, ya que a menudo habrá elecciones involucradas en formar el cierre de una gráfica (si más de un par de vértices satisfacen la condición, ¿qué borde agregamos primero?) , ¿es posible que al tomar diferentes elecciones, terminemos con una gráfica diferente al final? La respuesta, afortunadamente, es no; cualquier gráfica tiene un cierre único, como ahora vamos a probar.

Lema$\PageIndex{2}$

El cierre está bien definido. Es decir, cualquier gráfica tiene un cierre único.

Prueba

$(e_1, . . . , e_{\ell})$Sea una secuencia de aristas que podamos elegir para llegar al cierre de$G$, y dejar que el cierre resultante sea la gráfica$G_1$. Dejar$(f_1, . . . , f_m)$ ser otra secuencia de este tipo, y dejar que el cierre resultante sea la gráfica$G_2$. Demostraremos por inducción sobre$\ell$ eso para cada$1 ≤ i ≤ \ell, e_i ∈ \{f_1, . . . , f_m\}$. Usaremos$\{u_i , v+i\}$ para denotar los vértices finales de$e_i$.

Caso base:$\ell = 1$, por lo que solo$\{u_1, v_1\}$ se agrega$G$ el borde para formar$G_1$. Como este fue el primer borde agregado, debemos tener

\[d_G(u_1) + d_G(v_1) ≥ n\]

Ya que$G_2$ tiene todos los bordes de$G$, ciertamente debemos tener

\[d_{G_2} (u_1) + d_{G_2} (v_1) ≥ n.\]

Ya que$G_2$ es un cierre de$G$, no tiene par de aristas no adyacentes cuyas valencias sumen$n$ o superiores, por lo que$u_1$ deben ser adyacentes a$v_1$ in$G_2$. Como el borde no$u_1v_1$ estaba adentro$G$, debe estar adentro$\{f_1, . . . , f_m\}$. Esto completa la prueba del caso base.

Paso inductivo: Comenzamos con la hipótesis inductiva. $k ≥ 1$Sea arbitrario (con$k ≤ \ell$), y supongamos que

\[e_1, . . . , e_k ∈ \{f_1, . . . , f_m\}.\]

Considerar$e_{k+1} = \{u_{k+1}, v_{k+1}\}$. Dejar$G_0$ ser la gráfica obtenida sumando los bordes$e_1, . . . , e_k$ a$G$. Ya que$e_{k+1}$ se optó por agregar$G_0$ a la forma$G_1$, debe darse el caso de que

\[d_{G'}(u_{k+1}) + d_{G'}(v_{k+1}) ≥ n.\]

Por nuestra hipótesis de inducción, todos los bordes de también$G_0$ están adentro$G_2$, así que esto significa

\[d_{G_2}(u_{k+1}) + d_{G_2}(v_{k+1}) ≥ n.\]

Ya que$G_2$ es un cierre de$G$, no tiene par de aristas no adyacentes cuyas valencias sumen$n$ o superiores, por lo que$u_{k+1}$ deben ser adyacentes a$v_{k+1}$ in$G_2$. Como el borde no$e_{k+1}$ estaba adentro$G$, debe estar adentro$\{f_1, . . . , f_m\}$.

Por el Principio de Inducción Matemática,$G_2$ contiene todos los bordes de$G_1$. Como no había nada especial en$G_2$ lo distinto de$G_1$, podríamos usar la misma prueba para mostrar que$G_1$ contiene todos los bordes de$G_2$. Por lo tanto,$G_1$ y$G_2$ tienen los mismos bordes. Ya que también tienen los mismos vértices (los vértices de$G$), son la misma gráfica. Así, el cierre de cualquier gráfica es único.

Esto permitió a Bondy y Chvatal deducir el siguiente resultado, que es más fuerte que el de Dirac aunque como hemos visto la prueba no es significativamente diferente.

Teorema$\PageIndex{3}$

Una gráfica simple tiene un ciclo Hamilton si y sólo si su cierre tiene un ciclo Hamilton.

Prueba: Aplicar repetidamente Lemma 13.2.1.

Esto tiene un corolario muy bonito.

Corolario$\PageIndex{1}$

Una gráfica simple sobre al menos$3$ vértices cuyo cierre es completo, tiene un ciclo Hamilton.

Prueba: Esta es una consecuencia inmediata del Teorema 13.2.3 junto con el hecho (ver Ejercicio 13.2.1 (1)) de que cada gráfica completa en al menos$3$ vértices tiene un ciclo de Hamilton.

Ejercicio$\PageIndex{1}$

1) Demostrar por inducción que para cada$n ≥ 3$,$K_n$ tiene un ciclo Hamilton.

2) Encuentra el cierre de cada una de estas gráficas. ¿Se puede decir fácilmente por el cierre si la gráfica tiene o no un ciclo Hamilton?

a)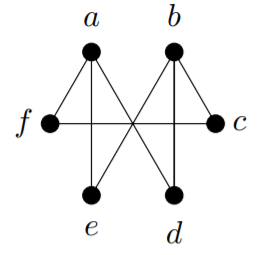 $clipboard_e3a43209a0e3ab890cb1dbaefb7b997bc.png$

b) $clipboard_e9f91fb4ac9a10ffb9a87ea0194077a1c.png$

3) Utilice el Teorema 13.2.1 para demostrar que esta gráfica no tiene un ciclo de Hamilton.

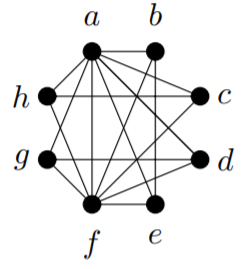
$clipboard_e6c98838b1ce95db5f794d050ec560220.png$

4) Demostrar que si$G$ tiene una ruta Hamilton, entonces para cada subconjunto adecuado no vacío$S$ de$V$, no$G − S$ tiene más que componentes$|S| + 1$ conectados.

5) Para las dos gráficas en el Ejercicio 13.2.1 (2), encuentre un ciclo de Hamilton o use el Teorema 13.2.1 para mostrar que no existe ningún ciclo de Hamilton.

Search

Text Color

Text Size

Margin Size

Font Type