14.3: Coloración de vértices

Última actualización
Guardar como PDF

Page ID: 114411

Joy Morris
University of Lethbridge

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Supongamos que se le ha dado la tarea de asignar frecuencias de difusión a torres de transmisión. Se le ha dado una lista de frecuencias que se le permite asignar. Hay una restricción: a las torres que están demasiado juntas no se les puede asignar la misma frecuencia, ya que interferirían entre sí.

Una forma de abordar este problema es modelarlo como una gráfica. Los vértices de la gráfica representarán las torres, y los bordes representarán torres que pueden interferir entre sí. Tu trabajo es asignar una frecuencia a cada uno de los vértices. En lugar de escribir una frecuencia en cada vértice, elegiremos un color para representar esa frecuencia, y usaremos ese color para colorear los vértices a los que asignes esa frecuencia.

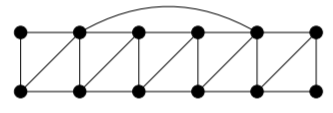
Aquí hay un ejemplo de ello.

Ejemplo$\PageIndex{1}$

Esta gráfica representa las torres y sus patrones de interferencia.

$clipboard_e8d83cbeaf0952764c72eb7a53422df4e.png$

Esto representa una posible asignación de$4$ colores a los vértices. El color de cada vértice (rojo, verde, azul o amarillo) se indica escribiendo la primera letra del nombre del color en el vértice).

$clipboard_eeb77390fd8f60f767aa564d4f7a2f92d.png$

Observe que esta coloración obedece a la restricción de que a las torres interferentes no se les asignan las mismas frecuencias.

Definición: Proper$k$-Vertex-Colouring

Una correcta coloración$k$ de vértices (o solo$k$ coloración) de una gráfica$G$ es una función que asigna a cada vértice de$G$ uno de los$k$ colores, de tal manera que a los vértices adyacentes se les deben asignar diferentes colores.

Al igual que con la coloración de bordes, la restricción de que los vértices adyacentes reciben diferentes colores resulta ser una restricción útil que surge en muchos contextos. A menudo representamos los$k$ colores por los números$1, . . . , k$, y etiquetamos los vértices con los números apropiados en lugar de colorearlos.

Definición:$k$-Colourable

Una gráfica$G$ es$k$ -coloreable si admite una coloración adecuada$k$ - (vértice-). El número entero más pequeño$k$ para$G$ el que es$k$ -coloreable se llama el número cromático de$G$.

Notación

El número cromático de$G$ se denota por$χ(G)$, o simplemente por$χ$ si el contexto es inequívoco.

Dejamos como ejercicio el comprobante de lo siguiente (ver Ejercicio 14.3.1 (2)).

Proposición$\PageIndex{1}$

Para cada$n ≥ 1$,$χ(K_n) = n$.

Ejemplo$\PageIndex{2}$

Demuéstralo para una gráfica$G$,$χ(G) = 2$ si y sólo si$G$ es una gráfica bipartita que tenga al menos una arista.

Solución

$(⇒)$Supongamos que$χ(G) = 2$. Tome una$2$ coloración adecuada de$G$ con colores$1$ y$2$. Dejar$V_1$ denotar el conjunto de vértices de color$1$, y dejar$V_2$ denotar el conjunto de vértices de color$2$. Dado que la coloración es apropiada, no hay bordes cuyos extremos estén en ambos extremos$V_1$ (ya que estos serían vértices adyacentes ambos coloreados con color$1$). Del mismo modo, no hay bordes cuyos vértices extremos estén en ambos extremos$V_2$. Así, los conjuntos$V_1$ y$V_2$ forman una bipartición de$G$, así$G$ es bipartita. Dado que los$2$ colores se requerían para colorear correctamente$G$,$G$ deben tener al menos un borde.

$(⇐)$Supongamos que$G$ es bipartito, y eso$V_1$ y$V_2$ formar una bipartición de$G$. Colorea los vértices$V_1$ con color$1$ y colorea los vértices$V_2$ con color$2$. Por la definición de una bipartición, no se puede haber asignado el mismo color a ningún par de vértices adyacentes. Por lo tanto, esta es una$2$ coloración adecuada de$G$, entonces$χ(G) ≤ 2$. Dado que$G$ tiene al menos una arista, a los extremos de esa arista se les deben asignar diferentes colores, así que$χ(G) ≥ 2$. Por lo tanto$χ(G) = 2$.

Ejemplo$\PageIndex{3}$

Demuéstralo para cualquier$n ≥ 1$,$χ(C_{2n+1}) = 3$.

Solución

Dado que esta gráfica tiene un borde cuyos endvertices deben tener asignados diferentes colores, lo vemos$χ(C_{2n+1}) ≥ 2$. Dado que un ciclo de longitud impar no es bipartito (ver Teorema 14.1.2), el Ejemplo 14.3.2 muestra que$χ(C_{2n+1}) \neq 2$, así$χ(C_{2n+1}) ≥ 3$. Que el ciclo sea$(u_1, u_2, . . . , u_{2n+1}, u_1)$. Dado que los únicos bordes en la gráfica están entre vértices consecutivos en esta lista, si asignamos color$2$ a$u_{2i}$$1 ≤ i ≤ n$, color$3$ a$u_{2i+1}$ para y color a para$1 ≤ i ≤ n$, este será un$3$ color adecuado.$1$$u_1$ Por lo tanto,$χ(C_{2n+1}) = 3$.

Definición:$k$-Critical

Una gráfica$G$ es k-crítica si$χ(G) = k$, pero para cada subgrafía adecuada$H$ de$G$,$χ(H) < χ(G)$.

Proposición$\PageIndex{2}$

Cualquier gráfico$k$ -crítico está conectado.

Prueba

Hacia una contradicción, supongamos que$G$ es un gráfico$k$ crítico desconectado, y dejar$G_1$ y$G_2$ ser (no vacíos) subgráficos de$G$ tal manera que cada vértice de$G$ está en cualquiera$G_1$ o$G_2$, y no hay borde de ningún vértice en$G_1$ ningún vértice en$G_2$. Por la definición de$k$ -crítico,$χ(G_1) < χ(G)$ y$χ(G_2) < χ(G)$. Pero si coloreamos$G_1$ con$χ(G_1)$ colores y$G_2$ con$χ(G_2)$ colores, ya que no hay borde de ningún vértice de$G_1$ a cualquier vértice de$G_2$, esto produce una coloración adecuada de$G$ con

\[\max(χ(G_1), χ(G_2)) < χ(G)\]

colores. Esta contradicción sirve para demostrar que cada gráfica$k$ -crítica está conectada.

Teorema$\PageIndex{1}$

Si$G$ es$k$ -crítico, entonces$δ(G) ≥ k − 1$.

Prueba: Hacia una contradicción, supongamos que eso$G$ es$k$ -crítico y tiene un vértice$v$ de valencia a lo sumo$k −2$. Por la definición de$k$ -crítico,$G \setminus \{v\}$ debe ser$(k −1)$ -coloreable. Ahora, dado que no$v$ tiene más que$k − 2$ vecinos, a sus vecinos se les pueden asignar como máximo colores$k − 2$ distintos en esta coloración. Por lo tanto, entre los colores utilizados en la$(k − 1)$ coloración de$G \setminus \{v\}$, debe haber un color que no se asigne a ninguno de los vecinos de$v$. Si asignamos este color a$v$, el resultado es una$(k − 1)$ coloración adecuada$G$, contradictoria$χ(G) = k$. Esta contradicción sirve para demostrar que cada gráfica$k$ -crítica tiene al menos una valencia mínima$k − 1$.

Corolario$\PageIndex{1}$

Para cualquier gráfica$G$,$χ(G) ≤ ∆(G) + 1$.

Prueba

$G$Déjese ser una gráfica arbitraria. Al eliminar tantos bordes y vértices como sea posible eliminar sin reducir el número cromático (nunca podremos aumentar el número cromático eliminando vértices o aristas, ver Ejercicio 14.3.1 (1)), vemos que$G$ debe tener un subgrafo$H$ que sea$χ(G)$ -crítico. Por el Teorema 14.3.1, vemos que

\[δ(H) ≥ χ(G) − 1.\]

Así, cada vértice de$H$ tiene valencia al menos$χ(G) − 1$, así que en$G$, estos mismos vértices todavía tienen valencia al menos$χ(G) − 1$. Para cualquier vértice de este tipo$v$, tenemos

\[∆(G) ≥ d(v) ≥ χ(G) − 1,\]

así$χ(G) ≤ ∆(G) + 1$.

Ya hemos visto dos familias de gráficas para las que se logra esta encuadernación: para gráficas completas, tenemos

\[∆(K_n) + 1 = (n − 1) + 1 = n = χ(K_n)\]

(ver Proposición 14.3.1); y para ciclos de longitud impar, tenemos

\[∆(C_{2n+1}) + 1 = 2 + 1 = 3 = χ(C_{2n+1})\]

(ver Ejemplo 14.3.3). De hecho, Brooks demostró en 1941 que estas son las únicas gráficas conectadas para las que se obtiene esta encuadernación.

Teorema$\PageIndex{2}$: Brook's Theorem

Si$G$ está conectado y para cada$n ≥ 1$,$G \ncong C_{2n+1}$ y$G \ncong K_n$, entonces$χ(G) ≤ ∆(G)$.

Prueba: No incluiremos la prueba de este resultado en este curso. Este teorema sí nos permite determinar el número cromático de algunas gráficas con muy poco trabajo.

Ejemplo$\PageIndex{4}$

La siguiente gráfica muy famosa se llama la gráfica Petersen. Es una gráfica excepcional en muchos sentidos, así que cuando los matemáticos están tratando de llegar a una prueba o un contraejemplo en la teoría de grafos, suele ser uno de los primeros ejemplos que van a comprobar. Encuentra su número cromático.

$clipboard_ec0db06837b987f121c2d381120de1ad0.png$

Solución

Tenemos$∆ = 3$, y como esta gráfica no es ni una gráfica completa ni un ciclo de longitud impar, según el Teorema de Brooks esto demuestra que$χ ≤ 3$. Podemos encontrar un ciclo de longitud$5$ alrededor del borde exterior de la gráfica, por lo que esta gráfica no es bipartita sino que tiene un borde. Por lo tanto (por Ejemplo 14.3.2),$χ > 2$. De ahí$χ = 3$.

Ejercicio$\PageIndex{1}$

1) Demostrar que si$H$ es un subgrafo de$G$ entonces$χ(G) ≥ χ(H)$.

2) Proprobar la Proposición 14.3.1 por inducción.

3) Probar Corolario 14.3.1 por inducción para cada gráfica en al menos un vértice.

4) Para cada uno$i$,$j ∈ \{4, 5, 6\}$, supongamos que se le da una gráfica$G$ que contiene una subgrafía isomórfica a$K_i$ y ningún vértice tiene más que$j$ vecinos. ¿De qué (si acaso) puedes decir$χ(G)$? ¿Puedes decir más si sabes que$G$ está conectado y no es ni una gráfica completa ni un ciclo de longitud impar?

Ejercicio$\PageIndex{2}$

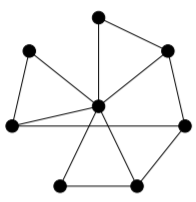
Para cada una de las siguientes gráficas, determinar su número cromático mediante el uso de argumentos teóricos para proporcionar un límite inferior, y luego producir una coloración que cumpla con el encuadernado. Haz lo mismo para el número cromático de borde.

1) $clipboard_ebb943566c31d45fb179a3e11db027e16.png$