1.3: Combinatoria y Teoría Gráfica

Una gráfica\(G\) consiste en un conjunto de vértices\(V\) y una colección\(E\) de subconjuntos de 2 elementos de\(V\). Los elementos de\(E\) se llaman bordes. En nuestro curso, vamos a utilizar (casi siempre) la convención que\(V=\{1,2,3,...,n\}\) para algún entero positivo\(n\). Con esta convención, las gráficas se pueden describir con precisión con un archivo de texto:

1. La primera línea del archivo contiene un solo entero\(n\), el número de vértices en la gráfica.
2. Cada una de las líneas restantes del archivo contiene un par de enteros distintos y especifica un borde de la gráfica.

Ilustramos esta convención en la Figura 1.2 con un archivo de texto y el diagrama para la gráfica\(G\) que define.

Figura\(\PageIndex{1.2}\): Un gráfico definido por datos

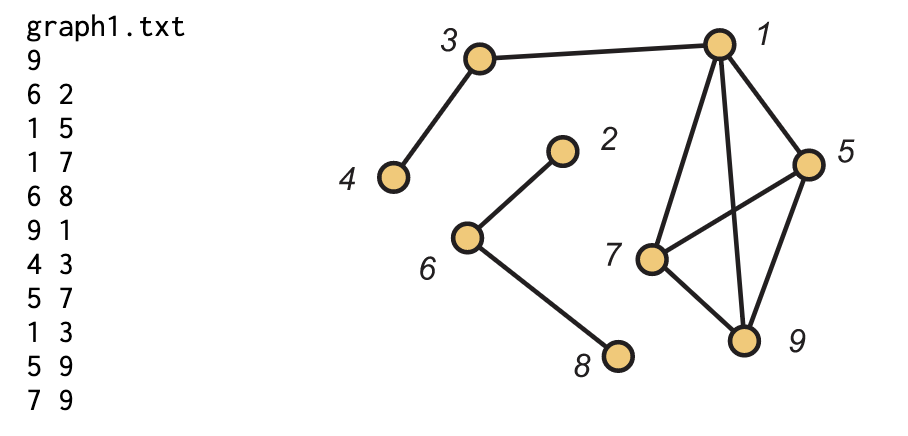
Gran parte de la notación y terminología para las gráficas es bastante natural. Vea si puede dar sentido a partir de las siguientes declaraciones que se aplican a la gráfica\(G\) definida anteriormente:

1. \(G\)tiene 9 vértices y 10 aristas.
2. \(\{2,6\}\)es un borde.
3. Los vértices 5 y 9 son adyacentes.
4. \(\{5,4\}\)no es un borde.
5. Los vértices 3 y 7 no son adyacentes.
6. \(P = (4,3,1,7,9,5)\)es una trayectoria de longitud 5 desde el vértice 4 hasta el vértice 5.
7. \(C = (5,9,7,1) \)es ciclo de longitud 4.
8. \(G\)está desconectado y tiene dos componentes. Uno de los componentes tiene conjunto de vértices\(\{2,6,8\}\).
9. \(\{1,5,7\}\)es un triángulo.
10. \(\{1,7,5,9\}\)es una camarilla de talla 4.
11. \(\{4,2,8,5\}\)es un conjunto independiente de tamaño 4.

Equipados solo con este poco de material de fondo, ya somos capaces de plantear una serie de problemas interesantes y desafiantes.

Ejemplo 1.3

Considera la gráfica que\(G\) se muestra en la Figura 1.4.

Figura\(\PageIndex{1.4}\): Un gráfico conectado

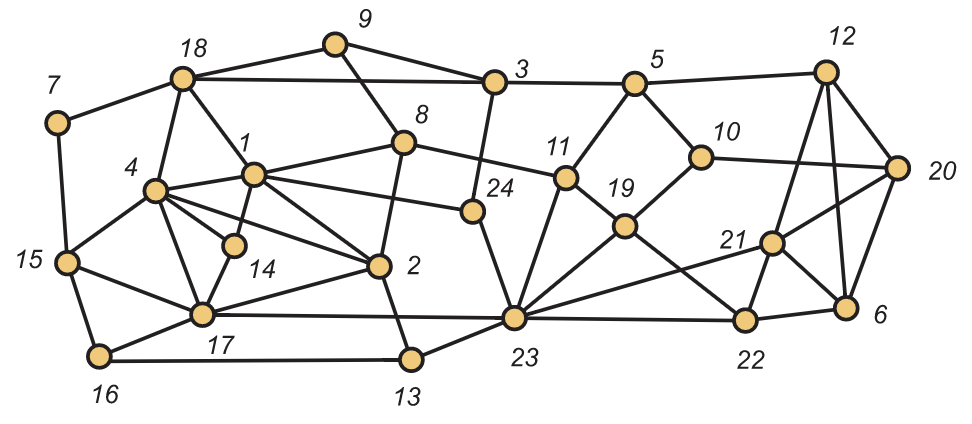
1. ¿Cuál es el mayor\(k\) para el que\(G\) tiene una trayectoria de longitud\(k\)?
2. ¿Cuál es el mayor\(k\) para el que\(G\) tiene un ciclo de duración\(k\)?
3. ¿Cuál es el más grande\(k\) para el que\(G\) tiene una camarilla de tamaño\(k\)?
4. ¿Cuál es el más grande\(k\) para el que\(G\) tiene un conjunto independiente de tamaño\(k\)?
5. ¿Cuál es el camino más corto del vértice 7 al vértice 6?

Supongamos que le dimos a la clase un archivo de datos de texto para una gráfica en 1500 vértices y preguntamos si la gráfica contiene un ciclo de longitud de al menos 500. Raoul dice que sí y Carla dice que no. ¿Cómo decidimos quién tiene razón?

Supongamos que en cambio preguntamos si la gráfica tiene una camarilla de tamaño 500. Helene dice que no lo cree, pero no está segura. ¿Es razonable que sus compañeras insistan en que ella tome una decisión, de una manera u otra? Es determinar si esta gráfica tiene una camarilla de tamaño 500 más dura, más fácil o más o menos lo mismo que determinar si tiene un ciclo de tamaño 500.

Frecuentemente estudiaremos problemas en los que las gráficas surgen de una manera muy natural. He aquí un ejemplo.

Ejemplo 1.5

En la Figura 1.6, se muestra la ubicación de algunas estaciones de radio en el avión, junto con una escala que indica una distancia de 200 millas. Las estaciones de radio que estén a menos de 200 millas de distancia deben transmitir en diferentes frecuencias para evitar interferencias.

Figura\(\PageIndex{1.6}\): Estaciones de radio

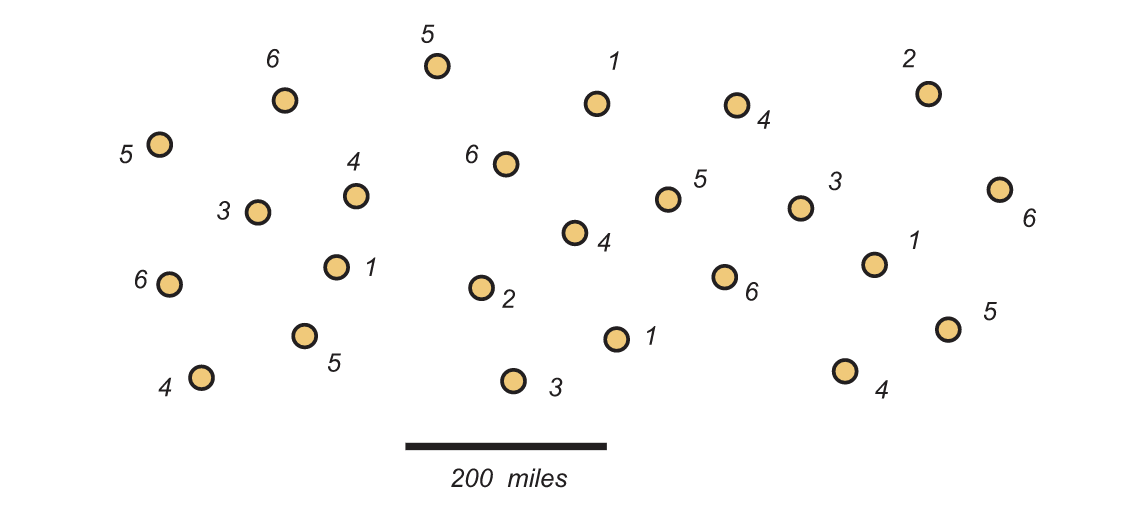
Hemos demostrado que son suficientes 6 frecuencias diferentes. ¿Puedes hacerlo mejor?

¿Puedes encontrar 4 estaciones cada una de las cuales se encuentra a 200 millas de las otras 3? ¿Puedes encontrar 8 estaciones cada una de ellas a más de 200 millas de distancia de las otras 7? ¿Existe una manera natural de definir una gráfica asociada a este problema?

Ejemplo 1.7

Qué tan grande debe ser una clase de combinatoria aplicada para que haya (a) seis alumnos con cada pareja habiendo tomado al menos otra clase juntos, o (b) seis estudiantes con cada pareja juntos en una clase por primera vez. ¿Es esto realmente un problema difícil o podemos resolverlo en solo unos minutos, garabateando en una servilleta?