2.1: Cuerdas- Un primer vistazo
- Page ID
- 118279
Dejar\(n\) ser un entero positivo. A lo largo de este texto, usaremos la notación\([n]\) taquigráfica para denotar el conjunto\(n\) -element\(\{1,2,...,n\}\). Ahora vamos a\(X\) ser un conjunto. Entonces una función también\(s:[n] \rightarrow X\) se llama una\(X\) -cadena de longitud\(n\). En las discusiones de\(X\) -cadenas, es costumbre referirse a los elementos de\(X\) como caracteres, mientras que el elemento\(s(i)\) es el\(i^{th}\) carácter de\(s\). Siempre que sea práctico, preferimos denotar una cadena\(s\) escribiendo\(s = "x_1x_2x_3...x_n"\), en lugar de la notación más engorrosa\(s(1) = x_1, s(2) = x_2, ..., s(n) = x_n\).
Hay una serie de alternativas para la notación y terminología asociadas a las cadenas. Primero, los caracteres de una cadena\(s\) se escriben frecuentemente usando subíndices como\(s_1,s_2,...,s_n\), por lo que el\(i^{th}\) término -term de se\(s\) puede denotar\(s_i\) en lugar de\(s(i)\). Las cadenas también se llaman secuencias, especialmente cuando\(X\) es un conjunto de números y la función\(s\) está definida por una regla algebraica. Por ejemplo, la secuencia de enteros impares se define por\(s_i = 2i - 1\).
Alternativamente, las cadenas se llaman palabras, el conjunto\(X\) se llama alfabeto y los elementos de\(X\) se llaman letras. Por ejemplo,\(aababbccabcbb\) es una palabra de 13 letras en el alfabeto de 3 letras\(\{a,b,c\}\).
En muchos lenguajes de computación, las cadenas se llaman matrices. Además, cuando el carácter\(s(i)\) está restringido para pertenecer a un subconjunto\(X_i \subseteq X\), una cadena puede considerarse como un elemento del producto cartesiano\(X_1 \times X_2 \times ... \times X_n\), que normalmente se ve como\(n\) -tuplas de la forma\((x_1,x_2,...,x_n)\) tal que\(x_i \in X_i\) para todos\(i \in [n]\).
En el estado de Georgia, las placas constan de cuatro dígitos seguidos de un espacio seguido de tres letras mayúsculas. El primer dígito no puede ser un 0. ¿Cuántas placas son posibles?
- Solución
-
Dejar\(X\) consistir en los dígitos\(\{0,1,2,...,9\}\), dejar\(Y\) ser el conjunto singleton cuyo único elemento es un espacio, y dejar\(Z\) denotar el conjunto de letras mayúsculas. Una placa válida es solo una cadena de
\((X - \{0\}) \times X \times X \times X \times Y \times Z \times Z \times Z\)
por lo que el número de placas diferentes es\(9 \times 10^3 \times 1 \times 26^3 = 158 184 000\), ya que el tamaño de un producto de juegos es el producto de los tamaños de los conjuntos. Podemos tener una idea de por qué este es el caso centrándonos solo en la parte del dígito de la cadena aquí. Podemos pensar en la porción de dígitos como cuatro espacios en blanco que necesitan ser llenados. El primer espacio en blanco tiene 9 opciones (los dígitos del 1 al 9). Si nos enfocamos solo en las cadenas de dígitos que comienzan con 1, una perspectiva es que van desde 1000 hasta 1999, por lo que hay 1000 de ellas. Sin embargo, también podríamos pensar en que hay 10 opciones para el segundo lugar, 10 opciones para el tercer lugar y 10 opciones para el cuarto. Multiplicando\(10 \times 10 \times 10\) da\(1000\). Dado que nuestro análisis de llenar los espacios en blanco de dígitos restantes no dependía de nuestra elección de un 1 para la primera posición, vemos que cada una de las 9 opciones de dígito inicial da 1000 cadenas, para un total de\(9000 = 9 \times 10^3 \).
En el caso de que\(X = \{0,1\}\), una\(X\) cadena -se denomina cadena 0-1 (también una cadena binaria o cadena de bits). Cuando\(X = \{0,1,2\}\), una\(X\) cadena -también se llama cadena ternaria.
Una instrucción de máquina en un sistema operativo de 32 bits es solo una cadena de bits de longitud 32. Así, hay 2 opciones para cada uno de los 32 puestos a llenar, haciendo el número de tales cadenas\(2^{32} = 4 294 967 296\). En general, el número de cadenas de bits de longitud\(n\) es\(2^n\).
Supongamos que un sitio web permite a sus usuarios elegir sus propios nombres de usuario para las cuentas, pero impone algunas restricciones. El primer carácter debe ser una letra mayúscula del alfabeto inglés. Los caracteres del segundo al sexto pueden ser letras (permitidas tanto en mayúsculas como en minúsculas) en el alfabeto inglés o dígitos decimales (0—9). La séptima posición debe ser '@' o '.'. Las posiciones octava a duodécima permiten letras inglesas minúsculas, '*', '%' y '#'. La decimotercera posición debe ser un dígito. ¿De cuántos usuarios puede aceptar registros el sitio web?
- Solución
-
Podemos visualizar las opciones pensando en las 13 posiciones en la cadena como espacios en blanco que necesitan ser rellenados y poniendo las opciones para ese espacio en blanco arriba. En la Figura 2.4, hemos usado U para denotar el conjunto de letras mayúsculas, L para el conjunto de letras minúsculas y D para el conjunto de dígitos.
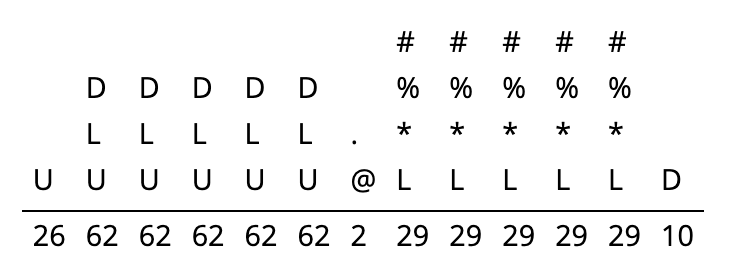
Figura 2.4: Plantilla de cadena Debajo de cada posición en la cadena, hemos escrito el número de opciones para esa posición. (Por ejemplo, hay 62 opciones para la segunda posición, ya que hay 52 letras una vez que se contabilizan ambos casos y 10 dígitos. Entonces multiplicamos estas posibilidades juntas, ya que cada elección es independiente de las demás. Por lo tanto, tenemos
\(26 \times 62^5 \times 2 \times 29^5 \times 10 = 9 771 287 890 863 360\)
total de nombres de usuario posibles.


