5.1: Notación y Terminología Básicas para Gráficas

Un gráfico\(G\) es un par\((V,E)\) donde\(V\) es un conjunto (casi siempre finito) y\(E\) es un conjunto de subconjuntos de 2 elementos de\(V\). Los elementos de\(V\) se llaman vértices y los elementos de\(E\) se llaman bordes. Llamamos\(V\) al conjunto de vértices de\(G\) y\(E\) es el conjunto de bordes. Para mayor comodidad, se acostumbra abreviar el borde\(\{x,y\}\) como justo\(xy\). Recuerda aunque eso\(xy \in E\) significa exactamente lo mismo que\(yx \in E\). Si\(x\) y\(y\) son vértices distintos de\(V, x\) y\(y\) son adyacentes cuando\(xy \in E\); de lo contrario, decimos que no son adyacentes. Decimos que el borde\(xy\) es incidente a los vértices\(x\) y\(y\).

Por ejemplo, podríamos definir una gráfica\(G=(V,E)\) con conjunto de vértices\(V=\{a,b,c,d,e\}\) y conjunto de bordes\(E=\{\{a,b\},\{c,d\},\{a,d\}\}\). Observe que ningún borde es incidente a, e, lo cual es perfectamente permisible en base a nuestra definición. Es bastante común identificar una gráfica con una visualización en la que dibujamos un punto para cada vértice y una línea que conecta dos vértices si son adyacentes. La gráfica\(G\) que acabamos de definir se muestra en la Figura 5.1. Es importante recordar que si bien un dibujo de una gráfica es una herramienta útil, no es lo mismo que la gráfica. Podríamos dibujar\(G\) en cualquiera de varias formas diferentes sin cambiar lo que es como gráfica.

Figura 5.1. Un gráfico en 5 vértices

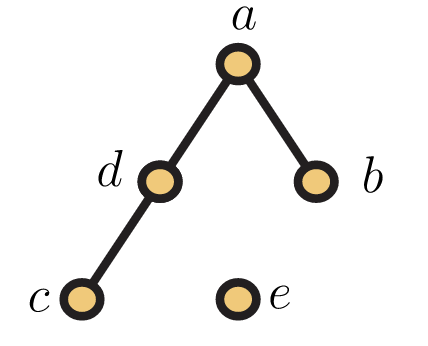
Como suele ser el caso en ciencias y matemáticas, diferentes autores utilizan notación y terminología ligeramente diferentes para las gráficas. Como ejemplo, algunos usan nodos y arcos en lugar de vértices y aristas. Otros se refieren a los vértices como puntos y en este caso, a menudo se refieren a líneas más que a aristas. Intentaremos apegarnos a vértices y aristas pero confesar que ocasionalmente podemos caer en referirnos a vértices como puntos. También, siguiendo los patrones de muchos otros, también diremos que los vértices adyacentes son vecinos. Y usaremos la terminología más o menos estándar que la vecindad de un vértice\(x\) es el conjunto de vértices adyacentes a\(x\). Así, usando la gráfica que\(G\) hemos representado en la Figura 5.1, los vértices\(d\) y\(a\) son vecinos, y el vecindario de\(d\) es\(\{a,c\}\) mientras que el vecindario de\(e\) es el conjunto vacío. También, el grado de un vértice\(v\) en una gráfica\(G\), denotado\(deg_G⁡(v)\), es entonces el número de vértices en su vecindad, o equivalentemente, el número de aristas que inciden en él. Por ejemplo, tenemos\(deg_G⁡(d)=deg_G⁡(a)=2, ,deg_G⁡(c)=deg_G⁡(b)=1\), y\(deg_G⁡(e)=0\). Si la gráfica que se está discutiendo es clara desde el contexto, no es raro omitir el subíndice y simplemente escribir\(deg⁡(v)\) para el grado de\(v\).

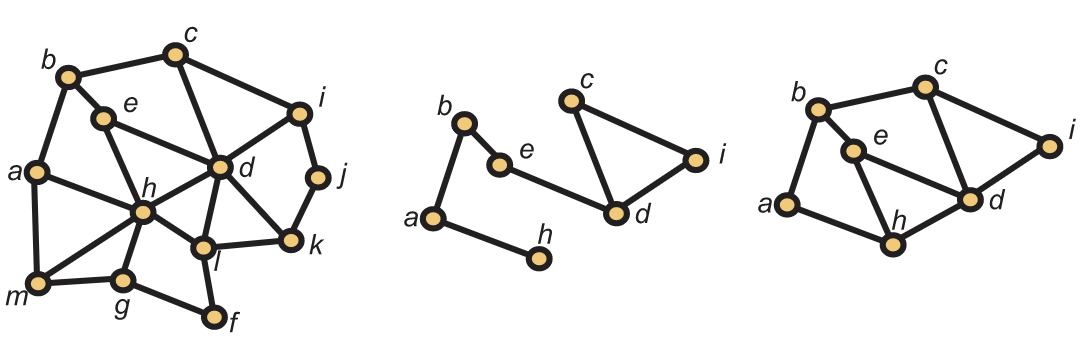
Cuando G\(= (V,E)\) y H\(= (W,F)\) son gráficas, decimos que H es un subgrafo de G cuando\(W \subseteq V\) y\(F \subseteq E\). Decimos que H es una subgrafía inducida cuando\(W \subseteq V\) y\(F=\{xy \in E:x,y \in W\}\). En otras palabras, una subgrafía inducida se define completamente por su conjunto de vértices y la gráfica original G. Decimos que H es un subgrafo abarcador cuando\(W=V\). En la Figura 5.2, se muestra una gráfica, una subgráfica y una subgráfica inducida. Ninguna de estas subgráficas es una subgráfica abarcadora.

Figura 5.2. Una Gráfica, una Subgrafía y una Subgrafía Inducida

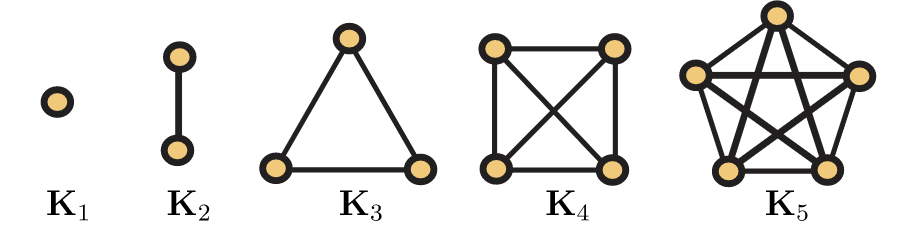
Una gráfica G\(=(V,E)\) se denomina gráfica completa cuando\(xy\) es un borde en G para cada par distinto\(x,y \in V\). Por el contrario, G es una gráfica independiente si\(xy \in E\), por cada par distinto\(x,y \in V\). Se acostumbra denotar una gráfica completa en\(n\) vértices por\(K_n\) y una gráfica independiente sobre\(n\) vértices por\(I_n\). En la Figura 5.3, se muestran las gráficas completas con como máximo 5 vértices.

Figura 5.3. Gráficas pequeñas y completas

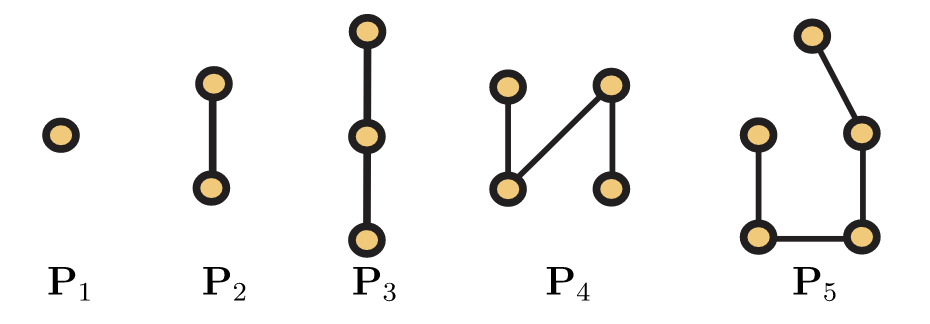
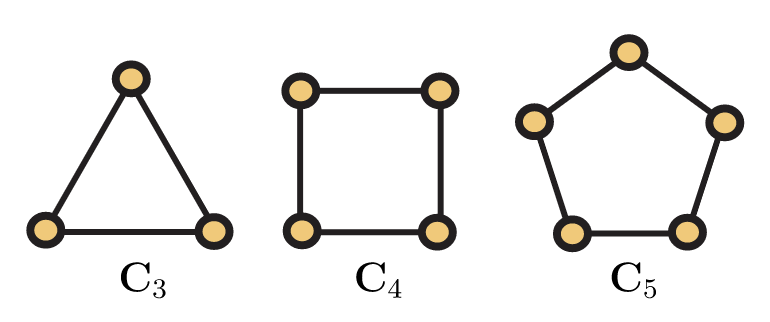
Una secuencia\((x_1,x_2,…,x_n)\) de vértices en una gráfica G =\((V,E)\) se llama paseo cuando\(x_ix_{i+1}\) es un borde para cada uno\(i=1,2,…,n−1\). Tenga en cuenta que los vértices en una caminata no necesitan ser distintos. Por otro lado, si los vértices son distintos, entonces la secuencia se llama camino, y muchas veces para enfatizar dónde comienza y termina un camino, diremos que una secuencia\((x_1,x_2,…,x_n)\) de vértices distintos es un camino de\(x_1\) a\(x_n\) en G. Del mismo modo\(n \geq 3\), cuando, una ruta\((x_1,x_2,…,x_n)\) de vértices\(n\) distintos se denomina ciclo cuando también\(x_1x_n\) es un borde en G. Se acostumbra denotar un camino en n vértices por\(P_n\), mientras que\(C_n\) denota un ciclo en\(n\) vértices. La longitud de un camino o un ciclo es el número de aristas que contiene. Por lo tanto, la longitud de\(P_n\) es\(n−1\) y la longitud de\(C_n\) es\(n\). En la Figura 5.4, mostramos los caminos de longitud como máximo 4, y en la Figura 5.5, mostramos los ciclos de longitud como máximo 5.

Figura 5.4. Caminos cortos

Figura 5.5. Ciclos pequeños

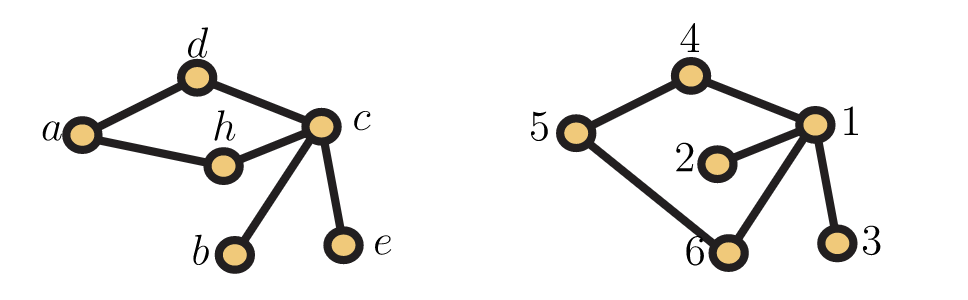
Si\(G = (V,E)\) y\(H = (W,F)\) son gráficas, decimos que\(G\) es isomórfico a\(H\) y escribimos\(G≅H\) cuando existe una biyección para\(f: V \xrightarrow[onto]{1-1} W\) que\(x\) sea adyacente a\(y\) in\(G\) si y solo si\(f(x)\) es adyacente a \(f(y)\)pulg\(H\). A menudo los escritores dirán que\(G\) “contiene”\(H\) cuando hay un subgrafo del\(G\) cual es isomorfo a\(H\). En particular, es costumbre decir que\(G\) contiene el ciclo\(C_n\) (mismo para\(P_n\) y\(K_n\)) cuando\(G\) contiene una subgrafía isomórfica a\(C_n\). Las gráficas de la Figura 5.6 son isomórficas. Un isomorfismo entre estas gráficas viene dado por

\(f(a) = 5, f(b) = 3, f(c)=1, f(d)=6, f(e)=2, f(h)=4\).

Figura 5.6. Un par de gráficas isomórficas

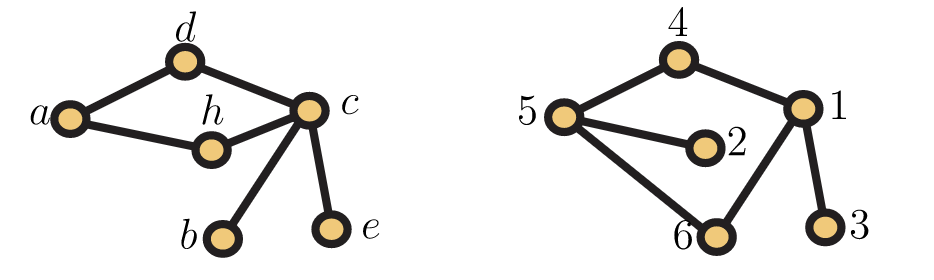
Por otro lado, las gráficas que se muestran en la Figura 5.7 no son isomórficas, aunque tengan el mismo número de vértices y el mismo número de aristas. ¿Se puede decir por qué?

Figura 5.7. Un par de gráficas no isomórficas

Una gráfica\(G\) se conecta cuando hay un camino de\(x\) a\(y\) adentro\(G\), para cada\(x,y \in V\); de lo contrario, decimos que\(G\) está desconectado. La gráfica de la Figura 5.1 está desconectada (una justificación suficiente para ello es que no hay camino de\(e\) a\(c\)), mientras que las de la Figura 5.6 están conectadas. Si\(G\) está desconectado, llamamos a un subgrafo conectado máximo de\(G\) un componente. Con esto queremos decir que un subgrafo\(H\) de\(G\) es un componente de\(G\) siempre que no exista un subgrafo conectado\(H′\) de\(G\) tal que\(H\) sea un subgrafo de\(H'\).

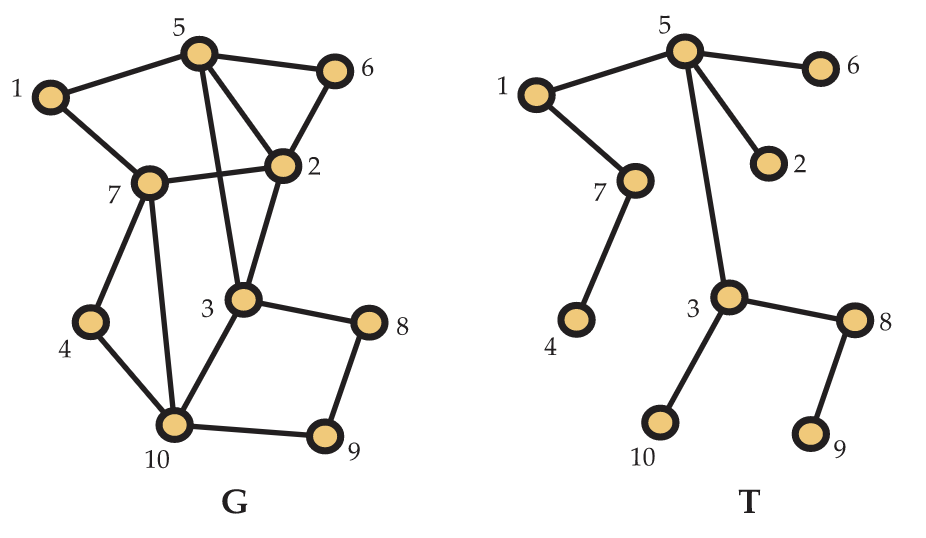
Una gráfica es acíclica cuando no contiene ningún ciclo en tres o más vértices. Las gráficas acíclicas también se llaman bosques. Una gráfica acíclica conectada se llama árbol. Cuando\(G=(V,E)\) es un grafo conectado, un subgrafo\(H=(W,F)\) de\(G\) se llama árbol de expansión si\(H\) es tanto un subgrafo de\(G\) expansión como un árbol. En la Figura 5.8, se muestra una gráfica y uno de sus árboles de expansión. Volveremos al tema de los árboles de expansión en el Capítulo 12.

Figura 5.8. Un gráfico y un árbol de expansión

El siguiente teorema es muy elemental, y algunos autores se refieren a él como el “primer teorema de la teoría gráfica”. Sin embargo, este resultado básico puede ser sorprendentemente útil.

Teorema 5.9.

Dejar\(degG⁡(v)\) denotar el grado de vértice\(v\) en la gráfica\(G=(V,E)\). Entonces

\(\displaystyle \sum_{v \in V} deg_G(v) = 2|E|\).

Prueba

Consideramos cuántas veces un borde\(e=vw \in E\) contribuye a cada lado de (5.1.1). Los\(deg_G⁡(y)\) términos\(deg_G⁡(x)\) y en el lado izquierdo cuentan cada uno\(e\) una vez, por lo que\(e\) se cuenta dos veces en ese lado. En el lado derecho,\(e\) se cuenta claramente dos veces. Por lo tanto, tenemos la igualdad reclamada.

Corolario 5.10.

Para cualquier gráfica, el número de vértices de grado impar es par.

Volveremos más adelante al tema de los árboles, pero antes de seguir adelante, probemos una proposición elemental sobre los árboles. Primero, una hoja en un árbol T es un vértice\(v\) con\(deg_T(v) = 1\).

Proposición 5.11

Cada árbol en\(n \geq 2\) vértices tiene al menos dos hojas.

Prueba

Nuestra prueba es por inducción en\(n\). Porque\(n=2\), hay precisamente un árbol, que es isomórfico a\(K_2\). Ambos vértices en esta gráfica son hojas, por lo que la proposición es válida\(n=2\). Ahora supongamos que para algún entero\(m \geq 2\), cada árbol en como máximo\(m\) vértices tiene al menos dos hojas y deja\(T=(V,E)\) ser un árbol sobre\(m+1\) vértices. Elija una arista\(e \in E\) y forme una nueva gráfica\(T′=(V′,E′)\) eliminando\(e\) de\(T\). Es decir,\(V′=V\) y\(E′=E−\{e\}\). Ahora como\(T′\) no contiene una ruta de un punto final de\(e\) a su otro punto final, no\(T′\) está conectado. Sin embargo, eliminar una arista no puede crear un ciclo, también lo\(T′\) es un bosque. Además, tiene precisamente dos componentes, cada uno de los cuales es un árbol con como máximo m vértices. Si cada componente tiene al menos dos vértices, entonces por inducción, cada uno tiene al menos dos hojas. En el peor de los casos, dos de estas hojas son los puntos finales de\(e\), por lo que al menos dos de los vértices son hojas adentro\(T\), también. Si cada componente de\(T′\) tiene solo un vértice, entonces\(T≅K_2\), que tiene dos hojas. Si exactamente uno de los componentes tiene un solo vértice, entonces debe ser una hoja adentro\(T\). Así, aplicar la hipótesis inductiva al otro componente asegura que haya una segunda hoja en\(T\).