5.9: Ejercicios
- Page ID
- 118442
- Las preguntas de este ejercicio pertenecen a la gráfica G que se muestra en la Figura 5.46.
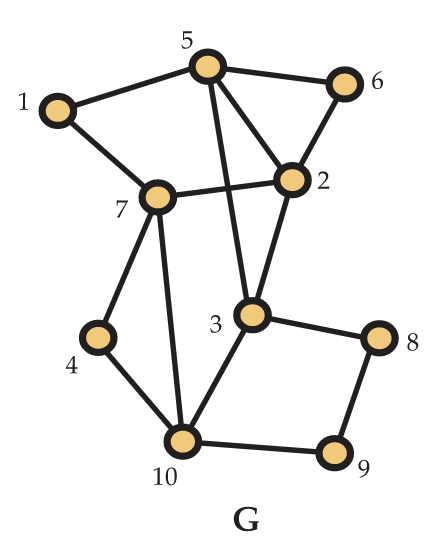
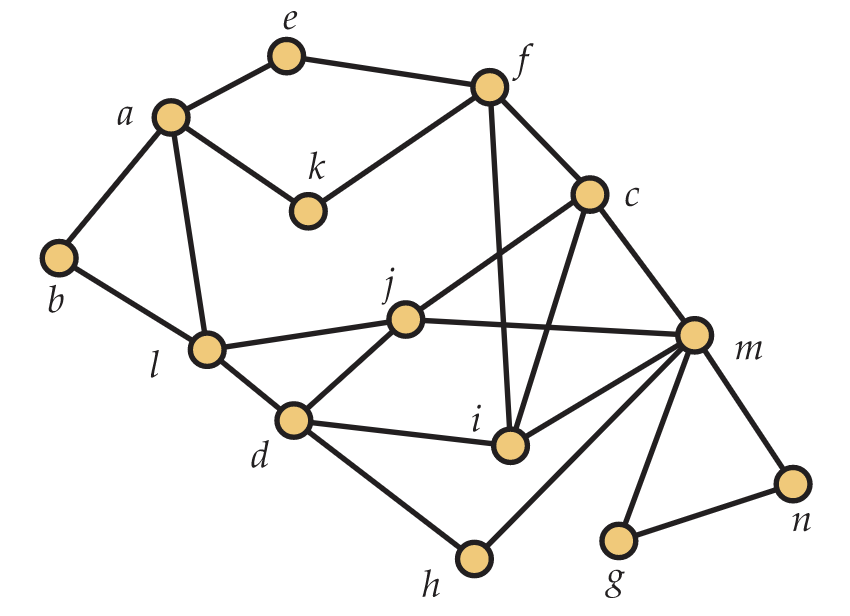
a. ¿Cuál es el grado de vértice 8?
b. ¿Cuál es el grado de vértice 10?
c. ¿Cuántos vértices de grado 2 hay en\(G\)? Enumerarlos.
d. encontrar un ciclo de 8 pulg\(G\).
e. ¿Cuál es la longitud de un camino más corto de 3 a 4?
f. ¿Cuál es la longitud de un camino más corto de 8 a 7?
g. Encuentra una trayectoria de longitud 5 desde el vértice 4 hasta el vértice 6.
2. Dibuja una gráfica con 8 vértices, todos de grado impar, que no contenga una trayectoria de longitud 3 o explique por qué no existe tal gráfica.
3. Dibuja una gráfica con 6 vértices que tengan grados 5, 4, 4, 2, 1 y 1 o explique por qué no existe tal gráfica.
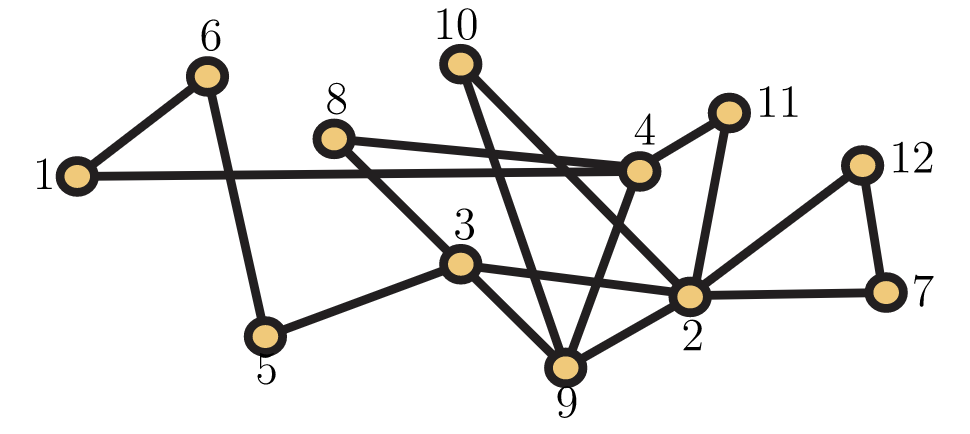
4. Para los próximos Juegos Olímpicos de Invierno, los organizadores desean ampliar el número de equipos que compiten en curling. Desean que entren 14 equipos, divididos en dos grupos de siete equipos cada uno. Ahora mismo, están pensando en exigir que en juego preliminar cada equipo juegue siete partidos contra distintos oponentes. Cinco de los oponentes vendrán de su propio grupo y dos de los oponentes vendrán del otro grupo. Están teniendo problemas para establecer un horario así, así que han acudido a ti. Mediante el uso de un modelo gráfico teórico apropiado, o bien argumentan que no pueden usar su plan actual o idear una manera para que lo hagan.
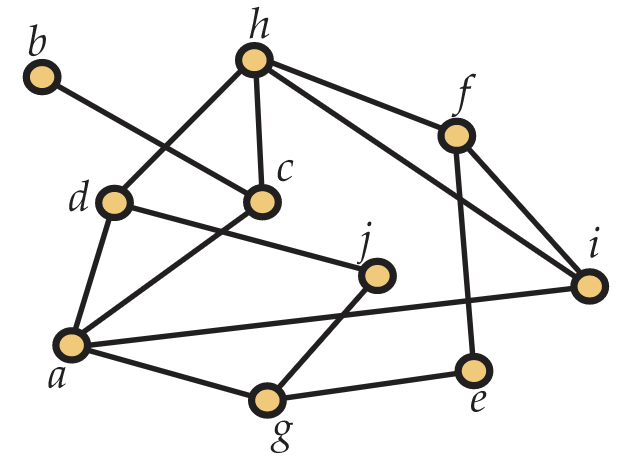
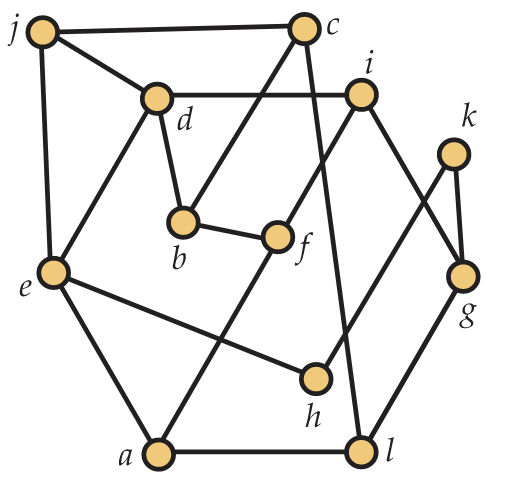
5. Para este ejercicio, considere la gráfica\(G\) en la Figura 5.47.
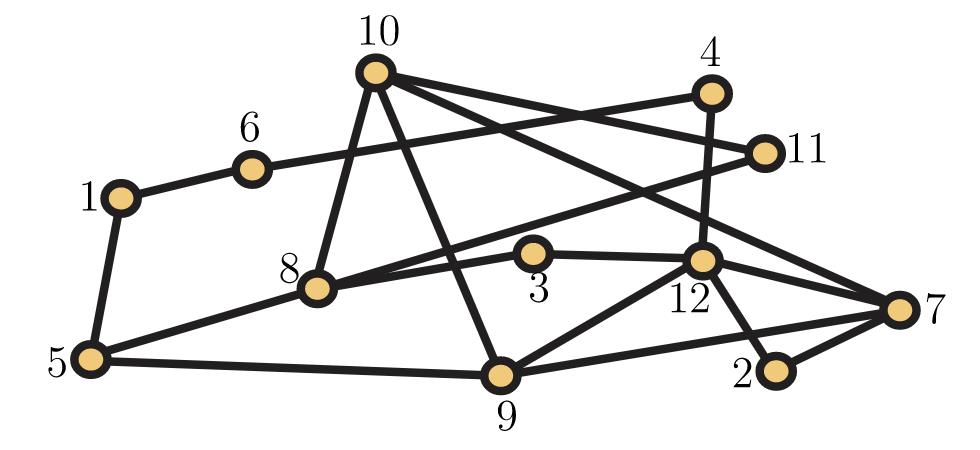
a. dejar\(V_1 = \{g,j,c,h,e,f\}\) y\(E_1 = \{ge,jg,ch,ef\}\). Es\((V_1, E_1)\) un subgrafo de\(G\)?
b. dejar\(V_2 = \{g,j,c,h,e,f\}\) y\(E_2 = \{ge,jg,ch,ef,cj\}\). Es\((V_2,E_2)\) un subgrafo de\(G\)?
c. Dejar\(V_3 = \{a,d,c,h,b\}\) y\(E_3 = \{ch,ac,ad,bc\}\). ¿Es\((V_3,E_3)\) una subgrafía inducida de\(G\)?
d. Dibujar el subgrafo de\(G\) inducido por\(\{g,j,d,a,c,i\}\).
e. Dibujar el subgrafo de\(G\) inducido por\(\{c,h,f,i,j\}\).
f. Dibujar un subgrafo de\(G\) tener un conjunto de vértices\(\{e,f,b,c,h,j\}\) que no sea un subgrafo inducido.
g. Dibuja un subgrafo de extensión\(G\) con exactamente 10 bordes.
6. Demostrar que cada árbol en\(n\) vértices tiene exactamente\(n−1\) bordes.
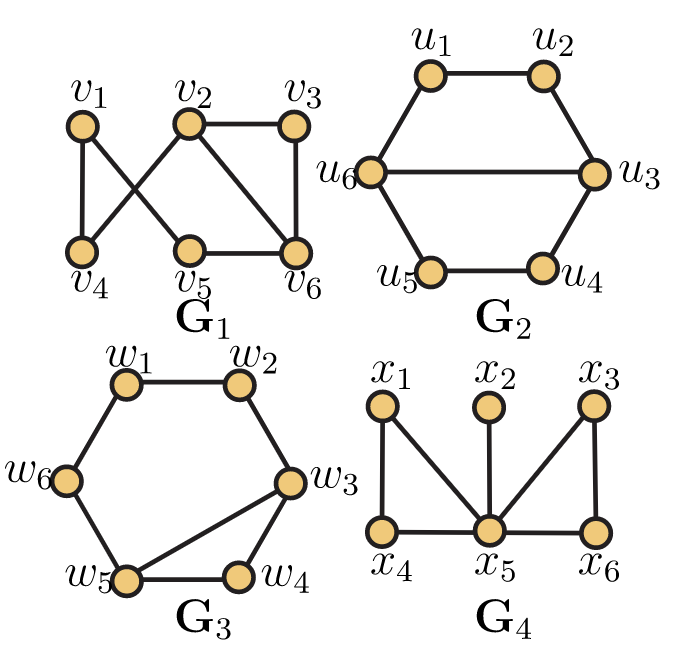
7. La Figura 5.48 contiene cuatro gráficas en seis vértices. Determinar cuáles (si los hay) pares de gráficos son isomórficos. Para los pares que son isomórficos, dar un isomorfismo entre las dos gráficas. Para parejas que no son isomórficas, explica por qué.
8. Encuentra un circuito euleriano en la gráfica\(G\) de la Figura 5.49 o explica por qué no existe uno.
9. Considera la gráfica\(G\) en la Figura 5.50. Determinar si la gráfica es euleriana. Si es así, encuentra un circuito euleriano. Si no lo es, explique por qué no lo es. Determinar si la gráfica es hamiltoniana. Si es así, encuentra un ciclo hamiltoniano. Si no lo es, explique por qué no lo es.
10. Explica por qué la gráfica\(G\) de la Figura 5.51 no tiene un circuito euleriano, sino que demuestra que al sumar un solo borde, puedes hacerlo euleriano.
11. Un sendero euleriano se define de la misma manera que un circuito euleriano (ver Sección 5.3) excepto que bajamos la condición de que\(x_0=x_t\). Demostrar que una gráfica tiene un rastro euleriano si y solo si está conectado y tiene como máximo dos vértices de grado impar.
12. Alice y Bob están discutiendo una gráfica que tiene 17 vértices y 129 aristas. Bob sostiene que la gráfica es hamiltoniana, mientras que Alice dice que se equivoca. Sin saber nada más sobre la gráfica, ¿uno de ellos debe tener razón? Si es así, ¿quién y por qué, y si no, por qué no?
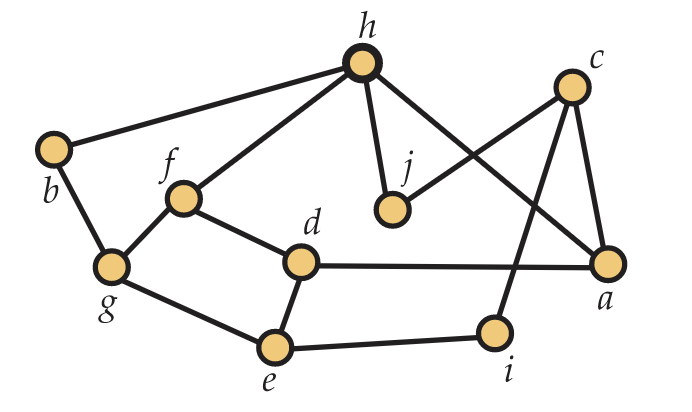
13. Encuentra el número cromático de la gráfica\(G\) en la Figura 5.52 y una coloración usando\(\chi(G)\) colores.
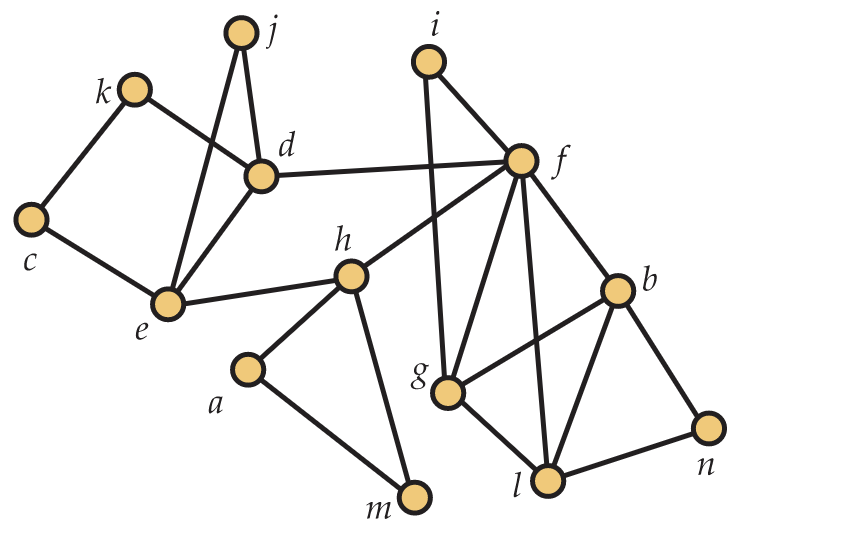
14. Encuentra el número cromático de la gráfica\(G\) en la Figura 5.53 y una coloración usando\(\chi(G)\) colores.
15. Un fabricante farmacéutico está construyendo un nuevo almacén para almacenar su suministro de 10 productos químicos que utiliza en la producción. Sin embargo, algunos de los químicos no se pueden almacenar en la misma habitación debido a reacciones indeseables que se producirán. La matriz de abajo tiene un 1 en posición\((i,j)\) si y sólo si\(j\) no se pueden almacenar químicos\(i\) y químicos en la misma habitación. Desarrollar un modelo teórico gráfico apropiado y determinar el menor número de habitaciones en las que pueden dividir su almacén para que puedan almacenar de manera segura los 10 productos químicos en el almacén.

16. Una escuela está preparando el horario de clases para el próximo curso académico. A ellos les preocupa programar clases de cálculo, física, inglés, estadística, economía, química y alemán, planeando ofrecer una sola sección de cada una. A continuación se presentan las listas de cursos que cada uno de los seis alumnos debe cursar para poder graduarse con éxito. Determinar el menor número de períodos de clase que se pueden utilizar para programar estos cursos si cada estudiante puede tomar como máximo un curso por período de clase. Explique por qué no se pueden utilizar menos periodos de clase.
| Alumno | Cursos |
| 1 | Química, Física, Economía |
| 2 | Inglés, Alemán, Estadísticas |
| 3 | Estadística, Cálculo, Alemán |
| 4 | Química, Física |
| 5 | Inglés, Química |
| 6 | Química, Economía |
17. Todos los árboles con más de un vértice tienen el mismo número cromático. ¿Qué es y por qué?
18. Encuentra una\((t+1)\) coloración adecuada de la gráfica\(G_{t+1}\) en la prueba de Mycielski de la Proposición 5.25. Esto establece que\(\chi(G_{t+1}) < t+1\).
19. ¿Cuántos vértices tiene la gráfica\(G_4\) de la prueba de Kelly y Kelly de la Proposición 5.25?
20. Construir y dibujar la gráfica\(G_5\) a partir de la prueba de Mycielski de la Proposición 5.25.
21. Encuentra una fórmula recursiva para el número de vértices nt en la gráfica\(G_t\) de la prueba de Kelly y Kelly de la Proposición 5.25.
22. \(b_t\)Sea el número de vértices en la gráfica\(G_t\) a partir de la prueba de Mycielski de la Proposición 5.25. Encuentra una fórmula recursiva para\(b_t\).
23. La circunferencia de una gráfica\(G\) es el número de vértices en un ciclo más corto de\(G\). Encuentra la circunferencia de la gráfica\(G_t\) en la prueba de Kelly y Kelly de la Proposición 5.25 y prueba que tu respuesta es correcta. Como reto, ver si se puede modificar la construcción de\(G_t\) para aumentar la circunferencia. Si es así, ¿hasta dónde puedes aumentarlo?
24. Utilice el algoritmo First Fit para colorear la gráfica de la Figura 5.26 usando los dos ordenamientos diferentes del conjunto de vértices que se muestra allí.
25. Dibuja la gráfica de intervalos correspondiente a los intervalos de la Figura 5.54.
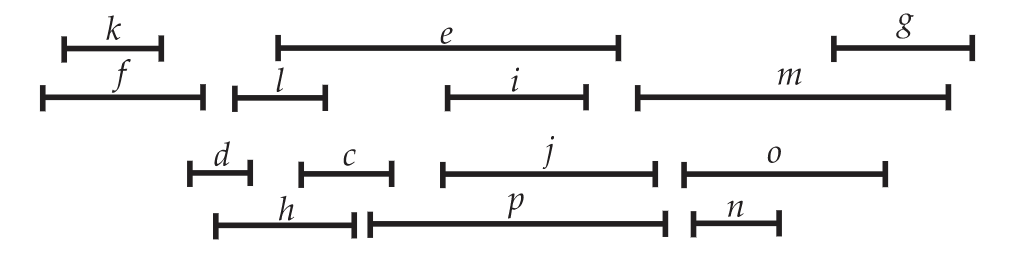
26. Utilice el algoritmo de coloración First Fit para encontrar el número cromático de la gráfica de intervalos cuya representación de intervalos se muestra en la Figura 5.54 así como una coloración adecuada utilizando la menor cantidad de colores posible.
27.
a. del Ejercicio 5.9.24 sabes que elegir un mal ordenamiento de los vértices de una gráfica puede llevar a que el algoritmo de coloración First Fit produzca una coloración que está lejos de ser óptima. Sin embargo, puedes usar este algoritmo para probar un límite en el número cromático. Demostrar que si cada vértice de\(G\) tiene grado como máximo\(D\), entonces\(\chi(G) \leq D + 1\).
b. Dar un ejemplo de una gráfica bipartita con\(D=1000\) para mostrar que este encuadernado no necesita ser ajustado.
28. ¿La gráfica de la Figura 5.53 es plana? Si es así, encuentra un dibujo sin cruces de bordes. Si no se da una razón por la que no lo es.
29. ¿La gráfica de la Figura 5.55 es plana? Si es así, encuentra un dibujo sin cruces de bordes. Si no se da una razón por la que no lo es.
30. Encuentra un dibujo plano de la gráfica\(K_{5−e}\), con lo cual nos referimos a la gráfica formada a partir de la gráfica completa en 5 vértices eliminando cualquier arista.
31. Exhibir un dibujo plano de una gráfica plana euleriana con 10 vértices y 21 aristas.
32. Demuestre que cada gráfico plano tiene un vértice que incide como máximo en cinco bordes.
33. Dejar\(G=(V,E)\) ser una gráfica con\(V=\{v_1,v_2,…,v_n\}\). Su secuencia de grados es la lista de los grados de sus vértices, dispuestos en orden no creciente. Es decir, la secuencia de grados de\(G\) es\((deg_G(v_1),deg_G(v_2),…,deg_G(v_n))\) con los vértices dispuestos de tal manera que\(deg_G(v_1) \geq deg_G(v_2) \geq \cdot \cdot \cdot \geq deg_G(v_n). Below are five sequences of integers (along with \(n\), el número de enteros en la secuencia). Identificar
- la única secuencia que no puede ser la secuencia de grados de ninguna gráfica
- las dos secuencias que podrían ser la secuencia de grados de una gráfica plana
- la única secuencia que podría ser la secuencia de grados de un árbol
- la única secuencia que es la secuencia de grados de una gráfica euleriana
- la única secuencia que es la secuencia de grados de una gráfica que debe ser hamiltoniana
Explique sus respuestas. (Tenga en cuenta que una secuencia obtendrá dos etiquetas desde arriba).
a.\(n=10: (4,4,2,2,1,1,1,1,1,1)\)
b.\(n=9: (8,8,8,6,4,4,4,4,4)\)
c.\(n=7: (5,4,4,3,2,1,0)\)
d.\(n=10: (7,7,6,6,6,6,5,5,5,5)\)
e.\(n=6: (5,4,3,2,2,2)\)
34. A continuación se presentan tres secuencias de longitud .10. Una de las secuencias no puede ser la secuencia de grados (ver Ejercicio 5.9.33) de ninguna gráfica. Identifíquelo y diga por qué. Para cada uno de los otros dos, di por qué (si tienes suficiente información) una gráfica conectada con esa secuencia de grados
- definitivamente es hamiltoniano/no puede ser hamiltoniano
- definitivamente es euleriano/no puede ser euleriano
- es definitivamente un árbol/no puede ser un árbol
- es definitivamente plano/no puede ser plano
(Si no tiene suficiente información para tomar una determinación para una secuencia sin tener gráficas específicas con esa secuencia de grados, escriba “no suficiente información” para esa propiedad).
a.\((6,6,4,4,4,4,2,2,2,2)\)
b.\((7,7,7,7,6,6,6,2,1,1)\)
c.\((8,6,4,4,4,3,2,2,1,1)\)
35. Para las secuencias de dos grados en el Ejercicio 5.9.34 que corresponden a gráficas, hubo algunas propiedades para las cuales la secuencia de grados no fue suficiente información para determinar si la gráfica tenía esa propiedad. Para cada una de esas situaciones, vea si puede dibujar tanto una gráfica que tenga la propiedad como una gráfica que no tenga la propiedad.
36. Dibuja los 16 árboles etiquetados en 4 vértices.
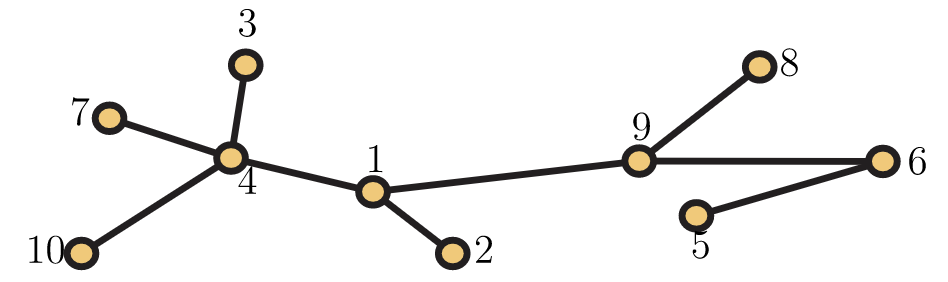
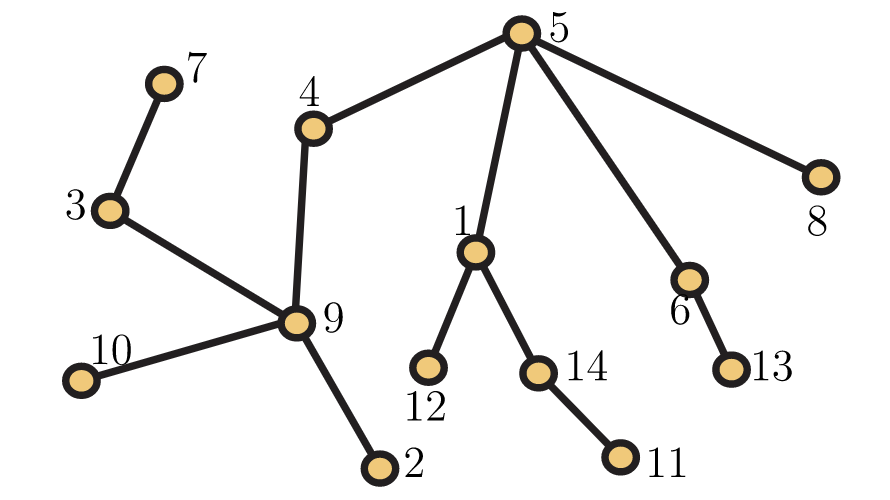
37. Determinar prüfer (T) para el árbol\(T\) en la Figura 5.56.
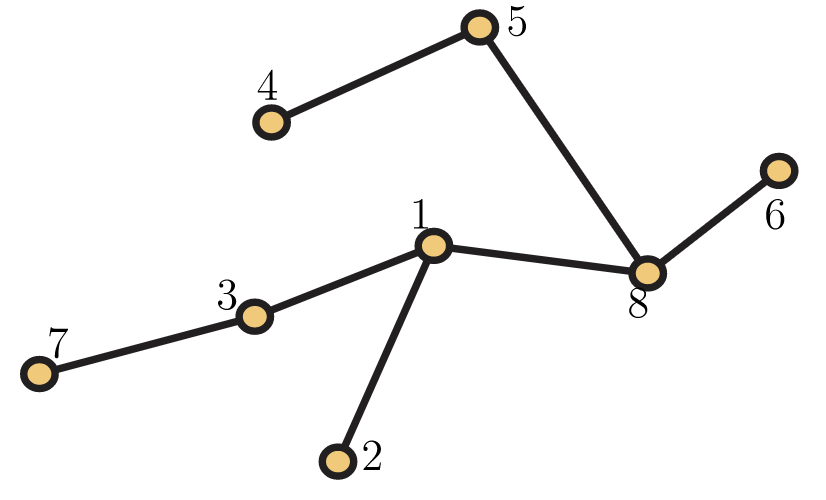
38. Determinar prüfer (T) para el árbol\(T\) en la Figura 5.57.
39. Determinar prüfer (T) para el árbol\(T\) Figura 5.58.
40. Construye el árbol etiquetado\(T\) con el código Prüfer 96113473.
41. Construye el árbol etiquetado\(T\) con el código Prüfer 23134.
42. Construye el árbol etiquetado\(T\) con código Prüfer (usando comas para separar símbolos en la cadena, ya que tenemos etiquetas mayores que 9)
\(10,1,7,4,3,4,10,2,2,8\)
43. (Problema de desafío)
Cuando\(G=(V,E)\) es una gráfica, vamos a\(Δ(G)\) denotar el grado máximo en\(G\). Demostrar el teorema de Brooks': Si\(G\) está conectado y\(Δ(G)=k\), entonces\(\chi(G) \leq k+1\). Además, la igualdad se mantiene si y sólo si (a)\(k=2\) y\(G\) es un ciclo impar, o (b)\(k \neq 2\) y\(G = K_{k+1}\).
- Pista
-
Es claro que\(\chi(G) \leq k+1\) (de hecho, esto ya estaba asignado como ejercicio). Supongamos que\(\chi(G)=k+1\) pero que ni la conclusión a) ni b) sostiene. Tome un árbol que abarca\(G\) y un orden apropiado de los vértices, con dos hojas del árbol primero. Después demuestre que una coloración First Fit de la gráfica solo utilizará\(k\) colores.


