7.1: Introducción

Última actualización
Guardar como PDF

Page ID: 118497

Mitchel T. Keller & William T. Trotter
Georgia Tech & Morningside College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Iniciamos este capítulo con un ejemplo elemental.

Ejemplo 7.1

$X$Sea el conjunto de 63 alumnos en un curso de combinatoria aplicada en una gran universidad tecnológica. Supongamos que hay 47 carreras de informática y 51 estudiantes varones. Además, sabemos que hay 45 estudiantes varones con especialización en ciencias de la computación. ¿Cuántos alumnos de la clase son mujeres estudiantes que no se especializan en ciencias de la computación?

Solución

Aunque los diagramas de Venn que probablemente hayas visto dibujados muchas veces a lo largo de los años no siempre son las mejores ilustraciones (especialmente si intentas pensar con algún tipo de escala), usemos uno para comenzar. En la Figura 7.2, vemos cómo los grupos en el escenario podrían superponerse.

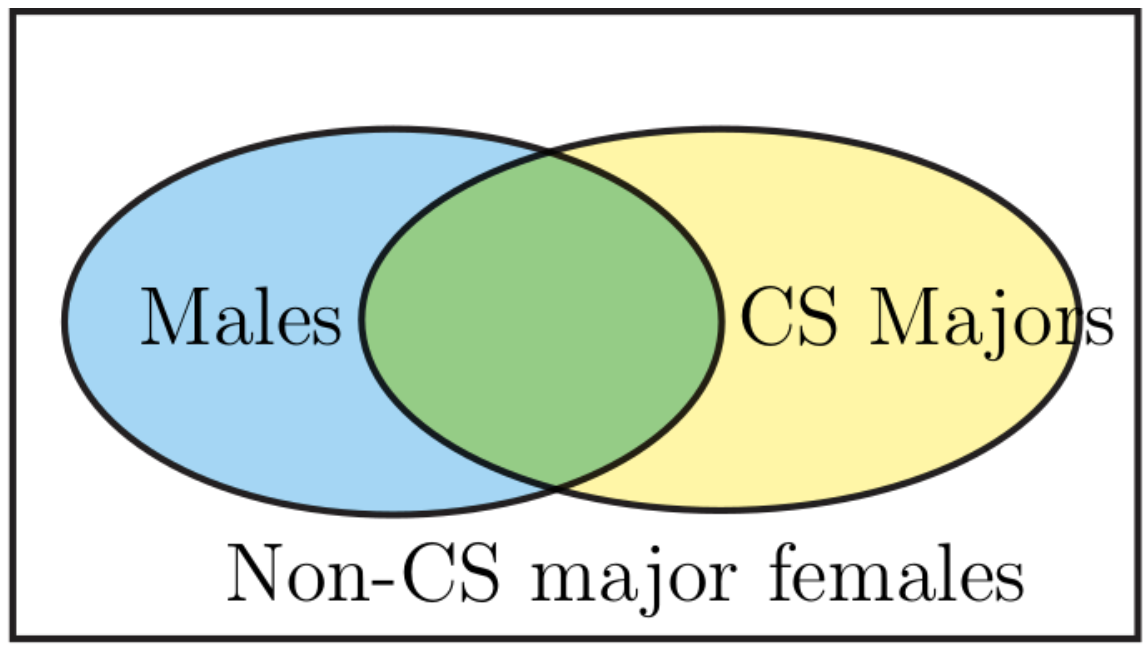
Screen Shot 2022-03-04 en 2.34.12 PM.png — Figura **7.2.** Un diagrama de Venn para una clase combinatoria aplicada

Ahora podemos ver que estamos tras el número de alumnos en el rectángulo blanco pero fuera de los dos óvalos sombreados, que son las alumnas que no se especializan en informática. Para calcular esto, podemos comenzar restando el número de estudiantes varones (la región azul) del número total de estudiantes en la clase y luego restando el número de carreras de ciencias de la computación (la región amarilla). Sin embargo, ahora hemos restado la región superpuesta (las carreras masculinas de informática) dos veces, por lo que debemos volver a sumar ese número. Así, el número de alumnas en la clase que no se especializan en informática es

$63-51-47+45=10$

Ejemplo 7.3

Otro tipo de problema donde podemos ver fácilmente cómo tal técnica es aplicable es una generalización del problema de enumerar soluciones enteras de ecuaciones. En el Capítulo 2, discutimos cómo contar el número de soluciones a una ecuación como

$x_1 + x_2 + x_3 + x_4 = 100$,

dónde$x_1>0, x_2,x_3 \geq 0$ y$2 \leq x_4 \leq 10$. No obstante, nos alejamos de la situación en la que agregamos la restricción adicional que$x_3 \leq 7$. El ejemplo anterior sugiere una manera de abordar este problema modificado.

Primero, vamos a configurar el problema para que el límite inferior de cada variable sea de la forma$x_i \geq 0$. Esto nos lleva al problema revisado de enumerar las soluciones enteras para

$x_1' + x_2 + x_3 + x_4' = 97$

con$x_1′,x_2,x_3,x_4′ \geq 0, x_3 \leq 7$, y$x_4′ \leq 8$. (Entonces tendremos$x_1=x_1′+1$ y$x_4=x_4′+2$ para obtener nuestra solución deseada.) Para contar el número de soluciones enteras a esta ecuación con$x_3 \leq 7$ y$x_4′ \leq 8$, debemos excluir cualquier solución en la que$x_3>7$ o$x_4′>8$. Hay$C(92,3)$ soluciones con$x_3>7$, y el número de soluciones en las que$x_4′>8$ se encuentra$C(91,3)$. En este punto, podría ser tentador simplemente restar$C(92,3)$ y$C(91,3)$ de$C(100,3)$, el número total de soluciones con todas las variables no negativas. Sin embargo, se requiere atención. Si lo hiciéramos, eliminaríamos las soluciones con ambos$x_3>7$ y$x_4′>8$ dos veces. Para dar cuenta de esto, notamos que hay$C(83,3)$ soluciones con ambos$x_3>7$ y$x_4′>8$. Si volvemos a sumar este número después de restar, nos hemos asegurado de que las soluciones con ambos$x_3>7$ y no$x_4′>8$ se incluyen en el recuento total y no se excluyen más de una vez. Así, el número total de soluciones es

$\dbinom{100}{3} - \dbinom{92}{3} - \dbinom{91}{3} + \dbinom{83}{3} = 6516$.

A partir de estos ejemplos, se debe comenzar a ver un patrón emergente que lleve a un escenario más general. En plena generalidad, consideraremos un conjunto$X$ y una familia$\mathcal{P}=\{P_1,P_2,…,P_m\}$ de propiedades. Tenemos la intención de que para todos$x \in X$ y cada uno$i=1,2,…,m$, o bien$x$ satisfaga$P_i$ o no lo hace. No hay ambigüedad. En última instancia, nos interesa determinar el número de elementos de los$X$ cuales no satisfacen ninguna de las propiedades en$\mathcal{P}$. En el Ejemplo 7.1, podríamos haber hecho que la propiedad$P_1$ “es una especialidad en informática” y la propiedad$P_2$ “es masculina”. Entonces el número de estudiantes que no satisfacen$P_1$ ni$P_2$ sería el número de alumnas que se especializan en algo distinto a la informática, exactamente el número que nos pidieron determinar. ¿Cuáles serían las propiedades$P_1$ y$P_2$ serían para el Ejemplo 7.3?

Consideremos tres ejemplos de conjuntos de propiedades más grandes. Estas propiedades volverán a aparecer durante el resto del capítulo a medida que aplicamos inclusión-exclusión a algunas situaciones más involucradas. Recordemos que a lo largo de este libro, utilizamos la notación$[n]$ para el conjunto$\{1,2,…,n\}$ cuando$n$ es un entero positivo.

Ejemplo 7.4

Dejar$m$ y$n$ ser fijos enteros positivos y dejar$X$ consistir en todas las funciones de$[n]$ a$[m]$. Entonces para cada uno$i=1,2,…,m$, y cada función$f \in X$, decimos que$f$ satisface$P_i$ si no hay$j$ así que eso$f(j)=i$. En otras palabras, no$i$ está en la imagen o salida de la función$f$.

Como ejemplo específico, supongamos que$n=5$ y$m=3$. Entonces la función dada por la siguiente tabla satisface$P_1$ pero no$P_2$ o$P_3$.

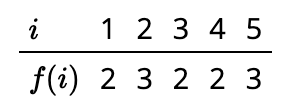
$Screen Shot 2022-03-04 en 2.47.42 PM.png$

Ejemplo 7.5

Dejar$m$ ser un entero positivo fijo y dejar$X$ consistir en todas las bijecciones de$[m]$ a$[m]$. Los elementos de$X$ se llaman permutaciones. Entonces para cada uno$i=1,2,…,m$, y cada permutación$ \sigma \in X$, decimos que$\sigma$ satisface$P_i$ si$\sigma(i)=i$.

Por ejemplo, la permutación$\sigma$ de$[5]$ dada en por la siguiente tabla satisface$P_3$ y$P_5$ y ninguna otra$P_i$.

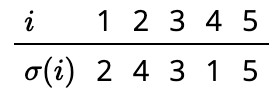
$Screen Shot 2022-03-04 en 2.52.26 PM.png$

Tenga en cuenta que en el ejemplo anterior, podríamos haber dicho que$\sigma$ satisface la propiedad$P_i$ si$\sigma(i) \neq i$. Pero recordando que nuestro objetivo es contar el número de elementos que satisfacen ninguna de las propiedades, entonces estaríamos contando el número de permutaciones satisfactorias$\sigma(i)=i$ para cada uno$i=1,2,…,n$, y tal vez no necesitamos mucha teoría para lograr esta tarea, el número es uno, por supuesto.

Ejemplo 7.6

Dejar$m$ y$n$ ser fijos enteros positivos y dejar$X=[n]$. Entonces para cada uno$i=1,2,…,m$, y cada uno$j \in X$, decimos que$j$ satisface$P_i$ si$i$ es un divisor de$j$. Dicho de otra manera, los enteros positivos que satisfacen la propiedad$P_i$ son precisamente aquellos que son múltiplos de$i$.

Al principio este puede parecer el más complicado de los conjuntos de propiedades que hemos discutido hasta ahora. No obstante, ser concreto debería ayudar a aclarar cualquier confusión. Supongamos que$n=m=15$. ¿Qué propiedades satisface 12? Los divisores de 12 son 1, 2, 3, 4, 6, y 12, por lo que 12 satisface$P_1, P_2, P_3, P_4, P_6$, y$P_{12}$. En el otro extremo del espectro, observe que 7 satisface sólo propiedades$P_1$ y$P_7$, ya que esos son sus únicos divisores.