7.7: Ejercicios

Última actualización
Guardar como PDF

Page ID: 118507

Mitchel T. Keller & William T. Trotter
Georgia Tech & Morningside College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1. Una escuela cuenta con 147 alumnos de tercer grado. Los maestros de tercer grado han planeado un regalo especial para el último día de clases y han traído helado para sus alumnos. Hay tres sabores: chip de menta, chocolate y fresa. Supongamos que a 60 estudiantes les gusta (al menos) las chispas de menta, a 103 les gusta el chocolate, a 50 les gustan las fresas, a 30 les gustan las chispas de menta y a la fresa, a 40 les gustan las chispas de menta y al chocolate, a 25 les gustan ¿A cuántos alumnos no les gusta ninguno de los sabores disponibles?

2. Hay 1189 estudiantes que se especializan en ciencias de la computación en una universidad en particular. Se les encuestó sobre su conocimiento de tres lenguajes de programación: C++, Java y Python. Los resultados de la encuesta reflejan que 856 estudiantes conocen C++, 792 conocen Java y 692 conocen Python. Adicionalmente, 639 estudiantes conocen tanto C++ como Java, 519 conocen tanto C++ como Python, y 632 conocen tanto Java como Python. Hay 488 alumnos que reportan conocer los tres idiomas. ¿Cuántos alumnos informaron que no conocían ninguno de los tres lenguajes de programación?

3. ¿Cuántos enteros positivos menores o iguales a 100 son divisibles por 2? ¿Cuántos enteros positivos menores o iguales a 100 son divisibles por 5? Utilice esta información para determinar cuántos enteros positivos menores o iguales a 100 no son divisibles ni por 2 ni por 5.

4. ¿Cuántos enteros positivos menores o iguales a 100 son divisibles por ninguno de 2, 3 y 5?

5. ¿Cuántos enteros positivos menores o iguales a 1000 son divisibles por ninguno de 3, 8 y 25?

6. El Estado de Georgia está distribuyendo 173 millones de dólares en fondos a los condados de Fulton, Gwinnett, DeKalb, Cobb y Clayton (en millones de dólares). ¿De cuántas maneras se puede hacer esta distribución, suponiendo que cada condado reciba al menos $1 millón, el condado de Clayton reciba como máximo $10 millones y el condado de Cobb reciba como máximo $30 millones? ¿Y si agregamos la restricción de que el condado de Fulton es recibir al menos 5 millones de dólares (en lugar de al menos $1 millón)?

7. ¿Cuántas soluciones enteras hay a la ecuación$x_1+x_2+x_3+x_4=32$ con$0 \leq x_i \leq 10$ for$i = 1,2,3,4$?

8. ¿Cuántas soluciones enteras hay para la desigualdad?

$y_1+y_2+y_3+y_4<184$

con$y_1>0$,$0<y_2 \leq 10$,$0 \leq y_3≤17$, y$0 \leq y_4<19$?

9. Un estudiante de posgrado almuerza en el patio de comidas del campus todos los martes en el transcurso de un semestre de 15 semanas. Se le une cada semana algún subconjunto de un grupo de seis amigos de todo el campus. En el transcurso de un semestre, comió con cada amigo 11 veces, cada par 9 veces, y cada triple 6 veces. Almorzó con cada grupo de cuatro amigos 4 veces y cada grupo de cinco amigos 4 veces. Los siete comieron juntos solo una vez ese semestre. ¿El estudiante de posgrado alguna vez almorzó solo? Si es así, ¿cuántas veces?

10. Se encuestó a un grupo de 268 estudiantes sobre su capacidad para hablar mandarín, coreano y japonés. Hay 37 alumnos que no hablan ninguno de los tres idiomas encuestados. El mandarín es hablado por 174 de los estudiantes, el japonés es hablado por 139 de los estudiantes, y el coreano es hablado por 112 de los estudiantes. Los resultados de la encuesta también reflejan que 102 estudiantes hablan mandarín y japonés, 81 estudiantes hablan mandarín y coreano, y 71 estudiantes hablan japonés y coreano. ¿Cuántos estudiantes hablan los tres idiomas?

11. Al igual que en el Ejemplo 7.4, let$X$ be the set of functions from$[n]$ to$[m]$ and let a function$f \in X$ satisfy property$P_i$ if there is not$j$ such that$f(j)=i$.

a. Que la función$f:[8] \rightarrow [7]$ sea definida por la Figura 7.18. ¿$f$Satisface la propiedad$P_2$? ¿Por qué o por qué no? ¿Qué pasa con la propiedad$P_3$? Listar todas las propiedades$P_i$ (con$i \leq 7$) satisfechas por$f$.

b. ¿Es posible definir una función$g:[8] \rightarrow [7]$ que no satisfaga ninguna propiedad$P_i$,$i \leq 7$? Si es así, dar un ejemplo. Si no, explica por qué no.

c. ¿Es posible definir una función$h:[8] \rightarrow [9]$ que no satisfaga ninguna propiedad$P_i$,$i \leq 9$? Si es así, dar un ejemplo. Si no, explica por qué no.

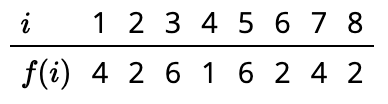
Screen Shot 2022-03-05 a las 12.14.56 PM.png — Figura **7.18.** Una función definida por una tabla

12. Al igual que en el Ejemplo 7.5, deja$X$ ser el conjunto de permutaciones de$[n]$ y decir que$\sigma \in X$ satisface la propiedad$P_i$ si$\sigma(i)=i$.

a. Que la permutación$\sigma:[8] \rightarrow [8]$ sea definida por la Figura 7.19. ¿La σ satisface la propiedad$P_2$? ¿Por qué o por qué no? ¿Qué pasa con la propiedad$P_6$? Listar todas las propiedades$P_i$ (con$i \leq 8$) satisfechas por$\sigma$.

b. Dar un ejemplo de una permutación$\mathcal{τ}:[8] \rightarrow [8]$ que satisfaga propiedades$P_1, P_4, and P_8$ y ninguna otra propiedad$P_i$ con$1 \leq i \leq 8$.

c. Dar un ejemplo de una permutación$\pi:[8] \rightarrow [8]$ que no satisfaga a ningún bien$P_i$ con$1 \leq i \leq 8$.

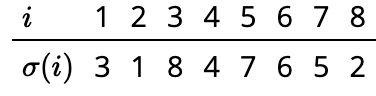
Screen Shot 2022-03-05 a las 12.20.55 PM.png — Figura **7.19.** Una permutación definida por una tabla

13. Al igual que en el Ejemplo 7.6, let$m$ y$n$ ser enteros positivos y$X=[n]$. Decir que$j \in X$ satisface propiedad$P_i$ para un$i$ con$1 \leq i \leq m$ si$i$ es un divisor de$j$.

a. vamos$m=n=15$. ¿12 satisface la propiedad$P_3$? ¿Por qué o por qué no? ¿Qué pasa con la propiedad$P_5$? Enumere las propiedades$P_i$ con$1 \leq i \leq 15$ que 12 satisfaga.

b. Dar un ejemplo de un entero$j$ con$1 \leq j \leq 15$ que satisfaga exactamente dos propiedades$P_i$ con$1 \leq i \leq 15$.

c. Dar un ejemplo de un entero$j$ con$1 \leq j \leq 15$ que satisfaga exactamente cuatro propiedades$P_i$ con$1 \leq i \leq 15$ o explicar por qué no existe tal entero.

d. Dé un ejemplo de un entero$j$ con$1 \leq j \leq 15$ que satisfaga exactamente tres propiedades$P_i$ con$1 \leq i \leq 15$ o explique por qué tal entero no existe.

14. ¿Cuántas surjecciones hay de un conjunto de ocho elementos a un conjunto de seis elementos?

15. Una maestra tiene 10 libros (todos diferentes) que quiere distribuir a John, Paul, Ringo y George, asegurando que cada uno de ellos obtenga al menos un libro. ¿De cuántas maneras puede hacer esto?

16. Un supervisor tiene nueve tareas que deben ser cumplidas y cinco empleados a quienes puede asignárselas. Si desea asegurarse de que a cada empleado se le asigne al menos una tarea a realizar, ¿cuántas formas hay de asignar las tareas a los empleados?

17. Un profesor está trabajando con seis estudiantes de investigación de pregrado. Tiene 12 temas que le gustaría que estos alumnos comiencen a investigar. Como ha estado trabajando con Katie durante varios términos, quiere asegurarse de que se le dé el tema más desafiante (y posiblemente otros). Sujeto a esto, ¿de cuántas formas puede asignar los temas a sus alumnos si a cada alumno se le debe asignar al menos un tema?

18. Enumere todos los desórdenes de$[4]$. (Por brevedad, puede escribir una permutación$\sigma$ como una cadena)$\sigma(1) \sigma(2) \sigma(3) \sigma(4)$.

19. ¿Cuántos desórdenes de un conjunto de nueve elementos hay?

20. El gerente de equipo de un equipo de futbol tiene prisa por distribuir uniformes a los seis últimos jugadores para presentarse antes de un partido. En lugar de asegurarse de que cada jugador reciba su propio uniforme, simplemente le entrega un uniforme a cada uno de los seis jugadores. ¿De cuántas maneras podría repartir los uniformes para que ningún jugador reciba su propio uniforme? (Supongamos que los seis uniformes restantes pertenecen a los últimos seis jugadores en llegar.)

21. Un empleado de nómina descuidado está colocando los cheques de pago de los empleados en sobres que han sido preetiquetados. Los sobres se sellan antes de que el secretario se dé cuenta de que no coincidió con los nombres en los cheques de pago con los nombres en los sobres. Si hay siete empleados, ¿de cuántas maneras podría haber colocado los cheques de pago en los sobres para que exactamente tres empleados reciban el cheque correcto?

22. El principio de inclusión-exclusión no es el único enfoque disponible para contabilizar los desórdenes. Eso lo sabemos$d_1=0$ y$d_2=1$. Utilizando esta información inicial, es posible dar una forma recursiva para$d_n$. En este ejercicio, consideramos dos recurrencias para$d_n$.

a. dar un argumento combinatorio para probar que el número de desórdenes satisface la fórmula recursiva$d_n=(n−1)(d_{n−1}+d_{n−2})$ para$n \geq 2$.

b. Demostrar que el número de desórdenes también satisface la fórmula recursiva$d_n=nd_{n−1}+(−1)^n$ para$n \geq 2$.

Pista

a. Para un desajuste$\sigma$, considere el entero$k$ con$\sigma(k)=1$. Argumentar con base en el número de opciones para$k$ y luego si$\sigma(1)=k$ o no.

b. Puede resultarle más fácil demostrarlo utilizando la otra fórmula recursiva e inducción matemática.

23. Determine$\phi(18)$ enumerando los enteros que cuenta así como usando la fórmula del Teorema 7.14.

24. Cómputos$\phi(756)$.

25. Teniendo en cuenta que$1625190883965792=(2)^5(3)^4(11)^2(13)(23)^3(181)^2$, computar

$\phi(1625190883965792)$.

26. Demostrar Proposición 7.15.

27. En una escuela muy pequeña, hay una clase con nueve alumnos en ella. Los alumnos, a quienes denotaremos como A, B, C, D, E, F, G, H y yo, caminan desde su salón de clases hasta el comedor en el orden ABCDEFGHI. (Digamos que A está al frente de la línea.) En el camino de regreso a su salón de clases después del almuerzo, les gustaría caminar en orden para que ningún estudiante camine inmediatamente detrás del mismo compañero de clase que él o ella estaba detrás de camino a almorzar. (Por ejemplo, ACBDIHGFE e IHGFEDCBA cumplirían con sus criterios. No obstante, no estarían contentos con CEFGBADHI ya que contiene FG y HI, por lo que G está siguiendo de nuevo a F y yo estoy siguiendo de nuevo a H.)

a. Un estudiante reflexiona sobre cuántas formas posibles habría para que se alineen cumpliendo con este criterio. Ayúdale determinando el valor exacto de este número.

b. ¿Este número es mayor, menor o igual al número de formas en que podrían regresar para que ningún alumno camine en la misma posición que antes (es decir, A no es el primero, B no es el segundo,..., y yo no es el último)?

c. ¿Qué fracción (darle como decimal) del número total de formas en las que podrían alinearse cumple con su criterio de que ningún estudiante siga inmediatamente detrás del mismo estudiante en el viaje de regreso?