9.1: Introducción
- Page ID
- 118570
9.1.1 Números de Fibonacci
Una de las recidivas más conocidas surge de una sencilla historia. Supongamos que un científico introduce a un par de conejos recién nacidos en una isla aislada. Esta especie de conejos es incapaz de reproducirse hasta su tercer mes de vida, pero después de eso produce un nuevo par de conejos cada mes. Así, en el primer y segundo meses, hay un par de conejos en la isla, pero en el tercer mes, hay dos parejas de conejos, ya que el primer par tiene un par de crías. En el cuarto mes, la pareja original de conejos sigue ahí, al igual que su primer par de crías, que aún no están lo suficientemente maduras para reproducirse. Sin embargo, la pareja original da a luz a otro par de conejos, lo que significa que la isla ahora tiene tres pares de conejos. Asumiendo que no hay depredadores que matan conejos en la isla y los conejos tienen una vida indefinida, ¿cuántas parejas de conejos hay en la isla en el décimo mes?
Veamos cómo podemos obtener una recurrencia a partir de esta historia. Que fn denote el número de parejas de conejos en la isla en mes\(n\). Así,\(f_1=1, f_2=1, f_3=2\), y\(f_4=3\) de nuestra cuenta anterior. ¿Cómo podemos computar\(f_n\)? Bueno, en el\(n^{th}\) mes tenemos todas las parejas de conejos que estuvieron ahí durante el mes anterior, que es\(f_{n−1}\); sin embargo, algunas de esas parejas de conejos también se reproducen durante este mes. Sólo los que nacieron antes del mes anterior son capaces de reproducirse durante el mes\(n\), por lo que hay\(f_{n−2}\) parejas de conejos que son capaces de reproducirse, y cada uno produce un nuevo par de conejos. Así, tenemos que el número de conejos en mes\(n\) es\(f_n=f_{n−1}+f_{n−2}\) para\(n \geq 3\) con\(f_1=f_2=1\). La secuencia de números {\(f_n:n \geq 0\)} (tomamos\(f_0=0\), que satisface nuestra recurrencia) se conoce como la secuencia de Fibonacci después de Leonardo de Pisa, más conocido como Fibonacci, un matemático italiano que vivió desde aproximadamente 1170 hasta aproximadamente 1250. Los términos\(f_0,f_1,…,f_{20}\) de la secuencia de Fibonacci son
\(0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765\).
Así, la respuesta a nuestra pregunta sobre el número de parejas de conejos en la isla en el décimo mes es de 55. Eso es realmente fácil de calcular, pero ¿y si pidiéramos el valor de\(f_{1000}\) en la secuencia de Fibonacci? ¿Podrías siquiera decir si la siguiente desigualdad es verdadera o falsa, sin realmente encontrarla\(f_{1000}\)?
\(f_{1000}<232748383849990383201823093383773932\)
Considerar la secuencia\(\{f_{n+1}/f_n:n \geq 1\}\) de proporciones de términos consecutivos de la secuencia de Fibonacci. La Figura 9.1 muestra estas proporciones para\(n \leq 18\).

Las proporciones parecen estar convergiendo a un número. ¿Podemos determinar este número? ¿Este número tiene algo que ver con una fórmula explícita para\(f_n\) (si existe alguna)?
La secuencia de Fibonacci no estaría tan bien estudiada como si solo fuera buena para contar parejas de conejos en una isla hipotética. Aquí hay otra instancia que nuevamente resulta en la secuencia de Fibonacci. Vamos a\(c_n\) contar el número de formas en que un\(2 \times n\) tablero de ajedrez puede ser cubierto por\(2 \times 1\) azulejos. Entonces\(c_1=1\) y\(c_2=2\) mientras la recurrencia es justa\(c_{n+2}=c_{n+1}+c_n\), ya que o bien la columna más a la derecha del tablero de ajedrez contiene un mosaico vertical (y por lo tanto el resto se puede enmarcar de\(c_{n+1}\) maneras) o las dos columnas más a la derecha contienen dos mosaicos horizontales (y así el resto de ella se puede enmarcar en \(c_n\)maneras).
9.1.2 Recurrencia para cadenas
En el Capítulo 3, vimos varias veces cómo podíamos encontrar recurrencias que nos dieron el número de cadenas binarias o ternarias de longitud\(n\) cuando colocamos una restricción sobre ciertos patrones que aparecen en la cadena. Recordemos un par de esos tipos de preguntas para ayudar a generar más recurrencias con las que trabajar.
Vamos a\(a_n\) contar el número de cadenas binarias de longitud\(n\) en las que no hay dos caracteres consecutivos 1. Evidentemente,\(a_1=2\) ya que ambas cadenas binarias de longitud 1 son “buenas”. Además,\(a_2=3\) ya que solo una de las cuatro cadenas binarias de longitud 2 es “mala”, es decir (1,1). Y\(a_3=5\), dado que de las 8 cadenas binarias de longitud 3, las siguientes tres cadenas son “malas”:
\((1,1,0),(0,1,1),(1,1,1)\).
De manera más general, es fácil ver que la secuencia satisface la recurrencia\(a_{n+2}=a_{n+1}+a_n\), ya que podemos particionar el conjunto de todas las cadenas “buenas” en dos conjuntos, las que terminan en 0 y las que terminan en 1. Si el último bit es 0, entonces en las primeras\(n+1\) posiciones, podemos tener cualquier cadena de longitud “buena”\(n+1\). Sin embargo, si el último bit es 1, entonces el bit anterior debe ser 0, y luego en las primeras\(n\) posiciones podemos tener cualquier cadena de longitud “buena”\(n\).
Como resultado, esta secuencia es solo los números de Fibonacci, aunque compensados por 1 posición, es decir,\(a_n=f_{n+1}\).
Vamos a\(t_n\) contar el número de cadenas ternarias en las que nunca tenemos (2,0) ocurriendo como una subcadena en dos posiciones consecutivas. Ahora\(t_1=3\) y\(t_2=8\), a partir de las 9 cuerdas ternarias de longitud 2, exactamente una de ellas es “mala”. Ahora considere el conjunto de todas las cadenas buenas agrupadas según el último carácter. Si este carácter es un 2 o un 1, entonces los\(n+1\) caracteres anteriores pueden ser cualquier cadena “buena” de longitud\(n+1\). Sin embargo, si el último carácter es un 0, entonces los primeros\(n+1\) caracteres forman una buena cadena de longitud\(n+1\) que no termina en un 2. El número de tales cadenas es\(t_{n+1}−t_n\). En consecuencia, la recurrencia es\(t_{n+2}=3t_{n+1}−t_n\). En particular,\(t_3=21\).
9.1.3 Líneas y regiones en el plano
Nuestro siguiente ejemplo nos lleva de vuelta a uno de los problemas motivadores discutidos en el Capítulo 1. En la Figura 9.5, se muestra una familia de 4 líneas en el plano. Cada par de líneas se cruza y ningún punto en el plano pertenece a más de dos líneas. Estas líneas determinan 11 regiones.
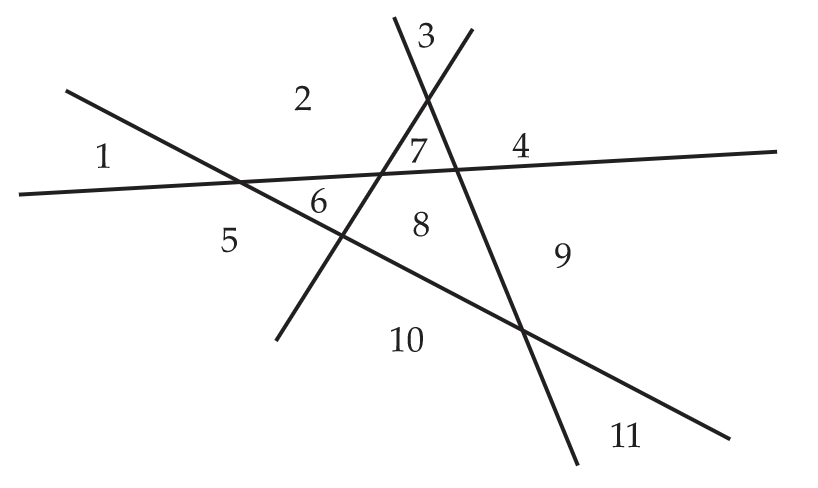
Nos preguntamos cuántas regiones determinaría una familia de 1000 líneas, dadas estas mismas restricciones sobre cómo se cruzan las líneas. De manera más general, vamos a\(r_n\) denotar el número de regiones determinadas por\(n\) líneas. Evidentemente,\(r_1=2, r_2=4, r_3=7\) y\(r_4=11\). Ahora es fácil ver que tenemos la recurrencia\(r_{n+1}=r_n+n+1\). Para ver esto, elige cualquiera de las\(n+1\) líneas y llámalo\(l\). La línea l cruza cada una de las otras líneas y dado que ningún punto en el plano pertenece a tres o más líneas, los puntos donde se\(l\) cruza con las otras líneas son distintos. Etiquetarlos consecutivamente como\(x_1,x_2,…,x_n\). Entonces estos puntos\(l\) dividen la línea en\(n+1\) segmentos, dos de los cuales (primero y último) son infinitos. Cada uno de estos segmentos divide una de las regiones determinadas por las otras\(n\) líneas en dos partes, lo que significa que tenemos las\(r_n\) regiones determinadas por las otras\(n\) líneas y\(n+1\) nuevas regiones que\(l\) crea.


