12.1: Árboles de expansión de peso mínimo
- Page ID
- 118513
En esta sección, consideramos pares\((\textbf{G},w)\) donde\(\textbf{G}=(V,E)\) es una gráfica conectada y\(w:E \rightarrow \mathbb{N}_0\). Para cada borde\(e \in E\), la cantidad\(w(e)\) se llama el peso de\(e\). Dado un conjunto\(S\) de aristas, definimos el peso de\(S\), denotado\(w(S)\), por ajuste\(w(S)= \sum_{e \in S} w(e)\). En particular, el peso de un árbol de expansión\(T\) es solo la suma de los pesos de los bordes en\(T\).
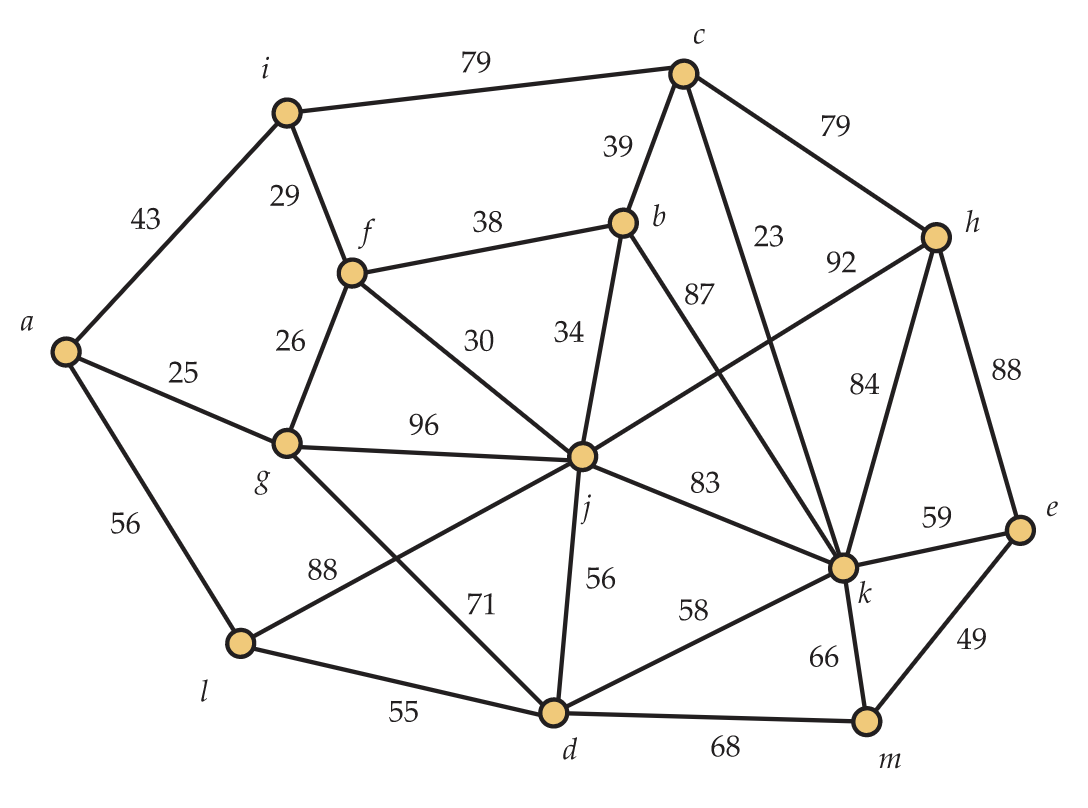
Las gráficas ponderadas surgen en muchos contextos. Una de las más naturales es cuando los pesos en los bordes son distancias o costos. Por ejemplo, considere la gráfica ponderada en la Figura 12.1. Supongamos que los vértices representan nodos de una red y los bordes representan la capacidad de establecer conexiones físicas directas entre esos nodos. Los pesos asociados a los bordes representan el costo (digamos en miles de dólares) de construir esas conexiones. A la compañía que establece la red entre los nodos solo le importa que haya una manera de obtener datos entre cada par de nodos. Cualquier enlace adicional crearía redundancia en la que no están interesados en este momento. Un árbol de expansión de la gráfica asegura que cada nodo pueda comunicarse con cada uno de los demás y no tenga redundancia, ya que al eliminar cualquier borde lo desconecta. Así, para minimizar el costo de construir la red, queremos encontrar un árbol de expansión de peso mínimo (o costo).
Para ello, esta sección considera el siguiente problema:
Encuentra un árbol que abarca el peso mínimo\(\textbf{T}\) de\(\textbf{G}\).
Para resolver este problema, desarrollaremos dos algoritmos de gráficos eficientes, cada uno con ciertas ventajas y desventajas computacionales. Antes de desarrollar los algoritmos, necesitamos establecer algunos preliminares sobre la expansión de árboles y bosques.
12.1.1 Preliminares
La siguiente proposición sobre el número de componentes en un bosque de expansión de una gráfica\(\textbf{G}\) tiene una prueba inductiva fácil. Se le pide que lo proporcione en los ejercicios.
Proposición 12.3
Dejar\(\textbf{G}=(V,E)\) ser una gráfica sobre\(n\) vértices, y dejar\(\textbf{H}=(V,S)\) ser un bosque que abarca. Entonces\(0 \leq |S| \leq n−1\). Además, si\(|S|=n−k\), entonces\(\textbf{H}\) tiene\(k\) componentes. En particular,\(\textbf{H}\) es un árbol de expansión si y sólo si contiene\(n−1\) aristas.
La siguiente propuesta establece una manera de tomar un árbol de expansión de una gráfica, eliminar una arista de ella y agregar una arista de la gráfica que no está en el árbol de expansión para crear un nuevo árbol de expansión. Efectivamente, el proceso intercambia dos aristas para formar el nuevo árbol de expansión, por lo que llamamos a esto el principio de intercambio.
Dejar\(\textbf{T}=(V,S)\) ser árbol de expansión en una gráfica\(\textbf{G}\), y dejar\(e=xy\) ser un borde del\(\textbf{G}\) cual no pertenece\(\textbf{T}\). Entonces
- Hay un camino único\(P=(x_0,x_1,x_2,…,x_t)\) con (a)\(x=x_0\) ; (b)\(y=x_t\) ; y (c)\(x_ix_{i+1} \in S\) para cada\(i=0,1,2,…,t−1\) .
- Para cada uno\(i=0,1,2,…,t−1\) , dejar\(f_i=x_ix_{i+1}\) y luego establecer
\(S_i = \{e\} \cup \{g \in S : g \neq f_i\}\),
es decir, intercambiamos borde\(f_i\) por borde\(e\). Entonces\(\textbf{T}_i=(V,S_i)\) es un árbol que abarca de\(\textbf{G}\).
- Prueba
-
Para el primer hecho, basta con señalar que si hubiera más de un camino distinto de\(x\) a\(y\) en\(\textbf{T}\), podríamos encontrar un ciclo en\(\textbf{T}\). Esto es imposible ya que es un árbol. Para el segundo, nos referimos a la Figura 12.5. Los bordes negro y verde en la gráfica que se muestra a la izquierda representan el árbol de expansión\(\textbf{T}\). Así,\(f\) yace en el camino único de\(x\) a\(y\) dentro\(\textbf{T}\) y\(e=xy\) es un borde de\(\textbf{G}\) no adentro\(\textbf{T}\). Agregar\(e\) a\(\textbf{T}\) crea una gráfica con un ciclo único, ya que\(\textbf{T}\) tenía un camino único desde\(x\) hasta\(y\). Quitar\(f\) (que podría ser cualquier borde\(f_i\) del camino, como se afirma en la proposición) destruye este ciclo. Así\(\textbf{T}_i\) es un subgrafo acíclico conectado de\(\textbf{G}\) con\(n−1+1−1=n−1\) bordes, por lo que es un árbol de expansión.
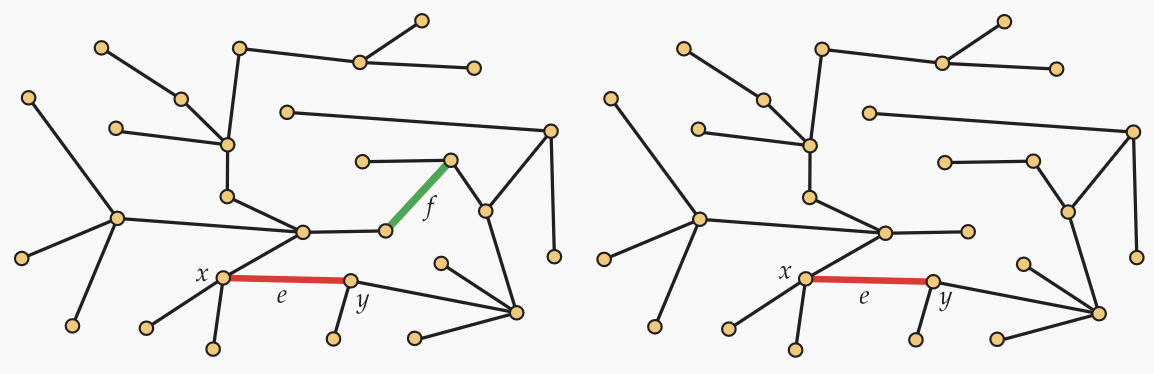
Figura 12.5. El principio de intercambio
Para ambos algoritmos que desarrollamos, el argumento para mostrar que el algoritmo es óptimo se basa en el siguiente lema técnico. Para evitar trivialidades, asumimos\(n \geq 3\).
Dejar\(\textbf{F}\) ser un bosque que abarca\(\textbf{G}\) y dejar\(C\) ser un componente de\(\textbf{F}\). También, deja\(e=xy\) ser un borde de peso mínimo entre todos los bordes con un punto final adentro\(C\) y el otro no adentro\(C\). Entonces entre todos los árboles que atraviesan\(\textbf{G}\) que contienen el bosque\(\textbf{F}\), hay uno de peso mínimo que contiene el borde\(e\).
- Prueba
-
\(\textbf{T}=(V,S)\)Sea cualquier árbol de expansión de peso mínimo entre todos los árboles de expansión que contienen el bosque\(\textbf{F}\), y supongamos que no\(e=xy\) es un borde en\(\textbf{T}\). (Si fuera una ventaja en\(\textbf{T}\), habríamos terminado.) Entonces deja\(P=(x_0,x_1,x_2,…,x_t)\) ser el camino único en\(\textbf{T}\) con (a)\(x=x_0\); (b)\(y=x_t\); y (c)\(x_ix_{i+1} \in S\) para cada uno\(i=0,1,2,…,t−1\). Sin pérdida de generalidad, podemos suponer que\(x=x_0\) es un vértice en el\(C\) tiempo que\(y=x_t\) no pertenece\(C\). Entonces hay un número entero menos no negativo\(i\) para el cual\(x_i\) está en\(C\) y no\(x_{i+1}\) está en\(C\). De ello se deduce que\(x_j\) está en\(C\) para todos\(j\) con\(0≤j≤i\).
Vamos\(f=x_ix_{i+1}\). El borde e tiene un peso mínimo entre todos los bordes con un punto final adentro\(C\) y el otro no adentro\(C\), entonces\(w(e)≤w(f)\). Ahora deja\(\textbf{T}_i\) ser el árbol obtenido intercambiando el borde\(f\) por borde\(e\). De ello se deduce que\(w(\textbf{T}_i)=w(\textbf{T})−w(f)+w(e)≤w(\textbf{T})\). Además,\(\textbf{T}_i\) contiene el bosque que abarca así\(\textbf{F}\) como el borde\(e\). Por lo tanto, es el árbol de expansión de peso mínimo que buscamos.
Aunque la intuición combinatoria de Bob ha mejorado a lo largo del curso, no entiende muy bien por qué necesitamos algoritmos especiales para encontrar árboles que abarcan el peso mínimo. Se da cuenta de que no puede haber tantos árboles que atraviesen, así que solo quiere escribirlos. Alice gime al sentir que Bob debió haber estado ausente cuando se discutió el material de la Sección 5.6. En esa sección, aprendimos que una gráfica sobre\(n\) vértices puede tener tantos como árboles de\(n^{n−2}\) expansión (u horrores, el instructor puede haberlo dejado fuera del plan de estudios). Independientemente, este enfoque exhaustivo ya es inutilizable cuando\(n=20\). Dave murmura algo sobre ser codicioso y simplemente agregar los bordes más ligeros uno por uno mientras nunca agrega un borde que haría un ciclo. Zori recuerda una estrategia como esta trabajando para encontrar la altura de un poset, pero está preocupada por la situación de pesadilla que aprendimos con el uso de FirstFit para colorear gráficos. Alice está de acuerdo en que los algoritmos codiciosos tienen un historial inconsistente pero sugiere que Lemma 12.6 puede ser suficiente para que uno tenga éxito aquí.
12.1.2 Algoritmo de Kruskal
En esta sección, desarrollamos uno de los algoritmos más conocidos para encontrar un árbol de expansión de peso mínimo. Se le conoce como Algoritmo de Kruskal, aunque algunos prefieren la etiqueta descriptiva Evitar Ciclos por la forma en que construye el árbol de expansión.
Para iniciar el algoritmo de Kruskal, ordenamos los bordes según el peso. Para ser más precisos, vamos a denotar m el número de aristas en\(\textbf{G}=(V,E)\). Después etiquetar los bordes como\(e_1,e_2,e_3,…,e_m\) para que\(w(e_1)≤w(e_2)≤ \cdot \cdot \cdot ≤w(e_m)\). Cualquiera de los muchos algoritmos de clasificación eficientes disponibles se puede utilizar para realizar este paso.
Una vez que se ordenan los bordes, el algoritmo de Kruskal procede a un paso de inicialización y luego construye inductivamente el árbol de expansión\(\textbf{T}=(V,S)\):
Inicialización. Set\(S = \emptyset\) y\(i = 0\)
Paso Inductivo. Mientras\(|S| < n - 1\), deja\(j\) ser el menor número entero no negativo para que\(j > i\) y no haya ciclos en\(S \cup \{e_j\}\). Luego (usando pseudo-código) establecer
\(i = j\)y\(S = S \cup \{j\}\).
La corrección del Algoritmo de Kruskal se desprende de un argumento inductivo. Primero, el conjunto\(S \) se inicializa como el conjunto vacío, por lo que ciertamente hay un árbol de expansión de peso mínimo que contiene todos los bordes en\(S\). Ahora supongamos que para algunos\(i\) con\(0≤i<n\),\(|S|=i\) y hay un árbol de expansión de peso mínimo que contiene todos los bordes en\(S\). Dejar\(\textbf{F}\) ser el bosque de expansión determinado por los bordes en\(S\), y dejar\(C_1,C_2,…,C_s\) ser los componentes de\(\textbf{F}\). Para cada uno\(k=1,2,…,s\), deje\(f_k\) ser un borde de peso mínimo con un punto final adentro\(C_k\) y el otro no adentro\(C_k\). Entonces el borde\(e\) agregado\(S\) por el Algoritmo de Kruskal es solo el borde\(\{f_1,f_2,…,f_s\}\) que tiene un peso mínimo. Aplicando Lema 12.6 y la hipótesis inductiva, sabemos que todavía habrá un árbol de expansión de peso mínimo de\(\textbf{G}\) contener todos los bordes de\(S \cup \{e\}\).
Veamos qué hace el algoritmo de Kruskal en la gráfica ponderada en la Figura 12.1. Primero ordena todos los bordes por peso. Aquí no vamos a reproducir la lista, ya que no la necesitaremos de toda. El borde de menor peso es\(ck\), que tiene peso 23. Continúa sumando el borde de menor peso, sumando\(ag, fg, fi, fj\), y\(bj\). No obstante, después de hacer esto, el borde de menor peso es\(fb\), que tiene peso 38. Este borde no se puede agregar, ya que hacerlo haría\(fjb\) un ciclo. Así, el algoritmo lo pasa por alto y agrega\(bc\). A continuación\(ai\) se inspecciona Edge, pero también crearía un ciclo y se elimina de la consideración. Después\(em\) se agrega, seguido de\(dl\). Ahora hay dos bordes de peso 56 a considerar:\(al\) y\(dj\). Nuestro algoritmo de clasificación de alguna manera ha decidido que uno de ellos debería aparecer primero, así que digamos que es\(dj\). Después de agregar\(dj\), no podemos agregar\(al\), como\(agfjdl\) formaría un ciclo. A continuación\(dk\) se considera Edge, pero también formaría un ciclo. Sin embargo, se\(ek\) pueden agregar. Bordes\(km\) y luego\(dm\) se pasan por alto. Finalmente, el borde\(ch\) se agrega como el duodécimo y último borde para este árbol de expansión de 13 vértices. La lista completa de aristas agregadas (en orden) se muestra a la derecha. El peso total de este árbol de expansión es 504.

12.1.3 Algoritmo de Prim
Ahora desarrollamos el Algoritmo de Prim para encontrar un árbol de expansión de peso mínimo. Este algoritmo también es conocido por una etiqueta más descriptiva: Build Tree. Comenzamos por elegir un vértice raíz\(r\). Nuevamente, el algoritmo procede con una etapa de inicialización seguida de una serie de pasos inductivos.
Inicialización. Set\(W = \{r\}\) y\(S = \emptyset\)
Paso Inductivo. Mientras\(|W| < n\), deja\(e\) ser un borde de peso mínimo entre todos los bordes con un punto final adentro\(W\) y el otro no adentro\(W\). Si\(e = xy, x \in W\) y\(y \notin W\), actualizar\(W\) y\(S\) configurando (usando pseudo-código)
\(W = W \cup \{y\}\)y\(S = S \cup \{e\}\).
La corrección del algoritmo de Prim sigue inmediatamente de Lemma 12.6.
Veamos qué hace el algoritmo de Prim en la gráfica ponderada en la Figura 12.1. Comenzamos con vértice\(a\) como vértice raíz. El borde más ligero que conecta\(a\) (el único vértice en el árbol hasta ahora) con el resto de la gráfica es\(ag\). A continuación,\(fg\) se agrega. Esto es seguido por\(fi, fj, bj\), y\(bc\). A continuación, el algoritmo se identifica\(ck\) como el borde más ligero\(\{a,g,i,f,j,b,c\}\) que se conecta a los vértices restantes. Observe que esto es considerablemente posterior a que el algoritmo de Kruskal encuentre el mismo borde. El algoritmo entonces determina eso\(al\) y\(jd\), ambos de peso 56 son los bordes más ligeros que conectan vértices en el árbol con los otros vértices. Se escoge arbitrariamente, así que digamos que se necesita\(al\). A continuación se encuentra\(dl\), entonces\(ek\), y después\(em\). El borde final agregado es\(ch\). La lista completa de aristas agregadas (en orden) se muestra a la derecha. El peso total de este árbol de expansión es 504. Este (no es sorprendente) el mismo peso que obtuvimos usando el algoritmo de Kruskal. Sin embargo, observe que el árbol de expansión encontrado es diferente, ya que este contiene al en lugar de\(dj\). Esto no es un problema, claro, ya que en ambos casos se hizo una elección arbitraria entre dos aristas de igual peso.
a g 25 f g 26 f i 29 f j 30 b j 34 b c 39 c k 23 a l 56 d l 55 e k 59 e m 49 c h 79
12.1.4 Comentarios en Eficiencia
Una implementación del algoritmo de Kruskal parece requerir que se ordenen los bordes. Si la gráfica tiene\(n\) vértices y\(m\) aristas, esto requiere\(m \log m\) operaciones solo para la ordenación. Pero una vez que se realiza la ordenación, el proceso solo toma\(n−1\) pasos, siempre que realice un seguimiento de los componentes a medida que se expande el bosque que abarca. Independientemente, es fácil ver que en la mayoría de\(O(n^2 \log n)\) las operaciones se requieren.
Por otro lado, una implementación del algoritmo de Prim requiere que el programa realice un seguimiento conveniente de los bordes incidentes con cada vértice y siempre sea capaz de identificar el borde con menor peso entre los subconjuntos de estos bordes. En informática, la estructura de datos que permite llevar a cabo esta tarea se denomina montón.


