12.3: Algoritmo de Dijkstra para caminos más cortos
- Page ID
- 118504
Al igual que con las gráficas, es útil asignar pesos a los bordes dirigidos de un dígrafo. Específicamente, en esta sección consideramos un par\((\textbf{G},w)\) donde\(\textbf{G}=(V,E)\) es un dígrafo y\(w:E \rightarrow \mathbb{N}_0\) es una función asignando a cada borde dirigido\((x,y)\) un peso no negativo\(w(x,y)\). Sin embargo, en esta sección, interpretamos el peso como distancia por lo que ahora\(w(x,y)\) se llama la longitud del borde\((x,y)\). Si\(P=(r=u_0,u_1,…,u_t=x)\) es una ruta dirigida de\(r\) a\(x\), entonces la longitud de la ruta\(P\) es solo la suma de las longitudes de los bordes en el camino,\(\sum_{i=0}^{t-1} w(u_iu_{i+1})\). La distancia desde\(r\) a\(x\) se define entonces para que sea la longitud mínima de una trayectoria dirigida desde\(r\) hasta\(x\). Nuestro objetivo en esta sección es resolver el siguiente problema natural, el cual tiene muchas aplicaciones:
Para cada vértice\(x\), encuentra la distancia de\(r\) a\(x\). También, encontrar un camino más corto de\(r\) a\(x\).
12.3.1 Descripción del Algoritmo
Para describir el algoritmo de Dijkstra de manera compacta, es útil ampliar la definición de la función\(w\). Hacemos esto configurando\(w(x,y)= \infty\) cuándo\(x \neq y\) y no\((x,y)\) es un borde dirigido de\(\textbf{G}\). De esta manera, trataremos\(\infty\) como si se tratara de un número (¡aunque no lo es!).
Ahora estamos preparados para describir el Algoritmo de Dijkstra.
Vamos\(n=|V|\). En Step\(i\)\(1≤i≤n\), donde, habremos determinado:
- Una secuencia\(σ=(v_1,v_2,v3,…,v_i)\) de vértices distintos de\(\textbf{G}\) con\(r=v_1\) . Estos vértices se denominan vértices permanentes, mientras que los vértices restantes se denominarán vértices temporales.
- Para cada vértice\(x∈V\) , habremos determinado un número\(δ(x)\) y una ruta\(P(x)\) de\(r\) a\(x\) de longitud \(δ(x)\).
Inicialización (Paso 1)
Set\(i=1\). Establecer\(δ(r)=0\) y dejar\(P(r)=(r)\) ser el camino trivial de un punto. También, set\(σ=(r)\). Para cada uno\(x≠r\), conjunto\(δ(x)=w(r,x)\) y\(P(x)=(r,x)\). Dejar\(x\) ser un vértice temporal para el cual\(δ(x)\) es mínimo. Establecer\(v_2=x\) y actualizar\(σ\) anexando\(v_2\) al final de la misma. Incremento\(i\).
Paso inductivo (paso\(i, i > 1\))
Si \(i<n\), entonces para cada temporal\(x\), vamos
\(δ(x)=min\{δ(x),δ(v_i)+w(v_i,x)\}\).
Si esta asignación resulta en una reducción en el valor de\(δ(x)\), deja\(P(x)\) ser la ruta obtenida sumando\(x\) al final de\(P(v_i)\).
Dejar\(x\) ser un vértice temporal para el cual\(δ(x)\) es mínimo. Establecer\(v_{i+1}=x\) y actualizar\(σ\) agregando\(v_{i+1}\) a él. Incremento\(i\).
12.3.2 Ejemplo del algoritmo de Dijkstra
Antes de establecer por qué funciona el algoritmo de Dijkstra, puede ser útil ver un ejemplo de cómo funciona. Para ello, considere el dígrafo que\(\textbf{G}\) se muestra en la Figura 12.15. Para mayor claridad visual, hemos elegido un dígrafo que es una gráfica orientada, es decir, para cada par distinto\(x,y\) de vértices, la gráfica contiene como máximo uno de los dos posibles bordes dirigidos\((x,y)\) y\((y,x)\).
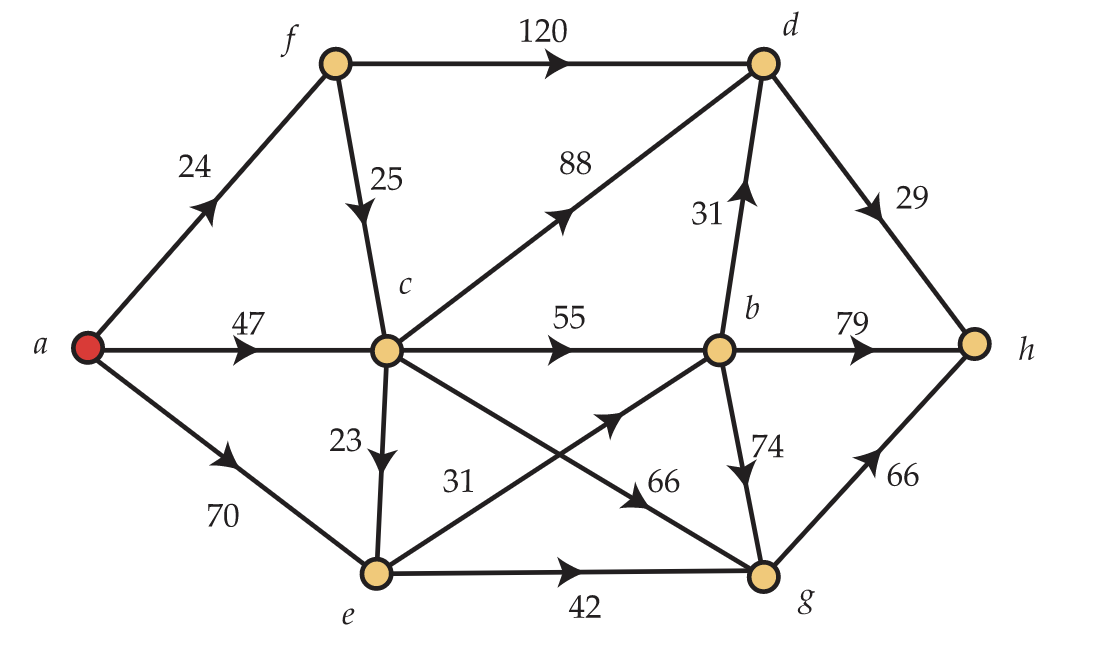
Supongamos que el vértice raíz\(r\) es el vértice etiquetado\(a\). El paso de inicialización del algoritmo de Dijkstra da como resultado los siguientes valores para\(δ\) y\(P\):
Paso 1. Inicialización.
\(σ=(a)\)
\(δ(a)=0;P(a)=(a)\)
\(δ(b)= \infty ;P(b)=(a,b)\)
\(δ(c)=47;P(c)=(a,c)\)
\(δ(d)= \infty ;P(d)=(a,d)\)
\(δ(e)=70;P(e)=(a,e)\)
\(δ(f)=24;P(f)=(a,f)\)
\(δ(g)= \infty ;P(g)=(a,g)\)
\(δ(h)= \infty ;P(h)=(a,h)\)
Antes de terminar el Paso 1, el algoritmo identifica el vértice\(f\) como el más cercano\(a\) y lo agrega\(σ\), haciéndolo\(a\) permanente. Al ingresar al Paso 2, el algoritmo de Dijkstra intenta encontrar caminos más cortos desde\(a\) hasta cada uno de los vértices temporales atravesando\(f\). A este proceso lo llamamos “escaneo desde vértice”\(f\). En este escaneo, se actualiza la ruta al vértice\(d\), ya que\(δ(f) + w(f,d) = 24 + 120 = 144 < \infty = w(a,d)\).
Paso 2. Escanear desde el vértice\(f\).
\(σ=(a,f)\)
\(δ(a)=0;P(a)=(a)\)
\(δ(b)= \infty;P(b)=(a,b)\)
\(δ(c)=47;P(c)=(a,c)\)
\(δ(d)=144=24+120=δ(f)+w(f,d);P(d)=(a,f,d)\)actualizado
\(δ(e)=70;P(e)=(a,e)\)
\(δ(f)=24;P(f)=(a,f)\)
\(δ(g)= \infty ;P(g)=(a,f)\)
\(δ(h)= \infty ;P(h)=(a,h)\)
Antes de pasar al siguiente paso, el vértice\(c\) se hace permanente al hacerlo\(v_3\). En el Paso 3, por lo tanto, el escaneo es de vértice\(c\). Vértices\(b, d\), y\(g\) tener sus caminos actualizados. Sin embargo, aunque\(δ(c)+w(c,e)=47+23=70=δ(e)\), no cambiamos\(P(e)\) ya que no\(δ(e)\) se disminuye por el enrutamiento\(P(e)\) a través\(c\).
Paso 3. Escanear desde el vértice\(c\).
\(σ=(a,f,c)\)
\(δ(a)=0;P(a)=(a)\)
\(δ(b)=102=47+55=δ(c)+w(c,b);P(b)=(a,c,b)\)actualizado
\(δ(c)=47;P(c)=(a,c)\)
\(δ(d)=135=47+88=δ(c)+w(c,d);P(d)=(a,c,d)\)actualizado
\(δ(e)=70;P(e)=(a,e)\)
\(δ(f)=24;P(f)=(a,f)\)
\(δ(g)=113=47+66=δ(c)+w(c,g);P(g)=(a,c,g)\)actualizado
\(δ(h)= \infty;P(h)=(a,h)\)
Ahora el vértice\(e\) se hace permanente.
Paso 4. Escanear desde el vértice e.
\(σ=(a,f,c,e)\)
\(δ(a)=0;P(a)=(a)\)
\(δ(b)=101=70+31=δ(e)+w(e,b);P(b)=(a,e,b)\)actualizado
\(δ(c)=47;P(c)=(a,c)\)
\(δ(d)=135;P(d)=(a,c,d)\)
\(δ(e)=70;P(e)=(a,e)\)
\(δ(f)=24;P(f)=(a,f)\)
\(δ(g)=112=70+42=δ(e)+w(e,g);P(g)=(a,e,g)\)actualizado
\(δ(h)= \infty;P(h)=(a,h)\)
Ahora el vértice\(b\) se hace permanente.
Paso 5. Escanear desde el vértice b.
\(σ=(a,f,c,e,b)\)
\(δ(a)=0;P(a)=(a)\)
\(δ(b)=101;P(b)=(a,e,b)\)
\(δ(c)=47;P(c)=(a,c)\)
\(δ(d)=132=101+31=δ(b)+w(b,d);P(d)=(a,e,b,d)\)actualizado
\(δ(e)=70;P(e)=(a,e)\)
\(δ(f)=24;P(f)=(a,f)\)
\(δ(g)=112;P(g)=(a,e,g)\)
\(δ(h)=180=101+79=δ(b)+w(b,h);P(h)=(a,e,b,h)\)actualizado
Ahora el vértice\(g\) se hace permanente.
Paso 6. Escanear desde el vértice g.
\(σ=(a,f,c,e,b,g)\)
\(δ(a)=0;P(a)=(a)\)
\(δ(b)=101;P(b)=(a,e,b)\)
\(δ(c)=47;P(c)=(a,c)\)
\(δ(d)=132;P(d)=(a,e,b,d)\)
\(δ(e)=70;P(e)=(a,e)\)
\(δ(f)=24;P(f)=(a,f)\)
\(δ(g)=112;P(g)=(a,e,g)\)
\(δ(h)=178=112+66=δ(g)+w(g,h);P(h)=(a,e,g,h)\)actualizado
Ahora el vértice\(d\) se hace permanente.Paso 7. Escanear desde el vértice d.
\(σ=(a,f,c,e,b,g,d)\)
\(δ(a)=0;P(a)=(a)\)
\(δ(b)=101;P(b)=(a,e,b)\)
\(δ(c)=47;P(c)=(a,c)\)
\(δ(d)=132;P(d)=(a,e,b,d)\)
\(δ(e)=70;P(e)=(a,e)\)
\(δ(f)=24;P(f)=(a,f)\)
\(δ(g)=112;P(g)=(a,e,g)\)
\(δ(h)=161=132+29=δ(d)+w(d,h);P(h)=(a,e,b,d,h)\)actualizado
Ahora el vértice\(h\) se hace permanente. Dado que este es el último vértice, el algoritmo se detiene y devuelve lo siguiente:
Resultados finales del Algoritmo de Dijkstra.
\(σ=(a,f,c,e,b,g,d,h)\)
\(δ(a)=0;P(a)=(a)\)
\(δ(b)=101;P(b)=(a,e,b)\)
\(δ(c)=47;P(c)=(a,c)\)
\(δ(d)=132;P(d)=(a,e,b,d)\)
\(δ(e)=70;P(e)=(a,e)\)
\(δ(f)=24;P(f)=(a,f)\)
\(δ(g)=112;P(g)=(a,e,g)\)
\(δ(h)=161;P(h)=(a,e,b,d,h)\)
12.3.3 La corrección del algoritmo de Dijkstra
Ahora que hemos ilustrado el algoritmo de Dijkstra, es hora de demostrar que realmente hace lo que afirmamos que hace: encontrar la distancia desde el vértice raíz a cada uno de los otros vértices y un camino de esa longitud. Para ello, primero señalamos dos proposiciones elementales. El primero es sobre los caminos más cortos en general, mientras que el segundo es específico de la secuencia de vértices permanentes producidos por el algoritmo de Dijkstra.
Dejar\(x\) ser un vértice y dejar\(P=(r=u_0,u_1,…,u_t=x)\) ser un camino más corto de\(r\) a\(x\). Entonces para cada entero\(j\) con\(0<j<t\),\((u_0,u_1,…,u_j)\) es un camino más corto de\(r\) a\(u_j\) y\((u_j,u_{j+1},…,u_t)\) es un camino más corto de\(u_j\) a\(u_t\)
Cuando el algoritmo se detiene, vamos\(σ=(v_1,v_2,v_3,…,v_n)\). Entonces
\(δ(v_1) \leq δ(v_2) \leq \cdot \cdot \cdot \leq δ(v_n)\).
Ahora estamos listos para probar la exactitud del algoritmo. La prueba que damos será inductiva, pero la inducción no tendrá nada que ver con el número total de vértices en el dígrafo o el número de paso en el que se encuentra el algoritmo.
El algoritmo de Dijkstra produce las rutas más cortas para cada vértice\(x\) en\(\textbf{G}\). Es decir, cuando el algoritmo de Dijkstra termina, para cada uno\(x \in V\), el valor\(δ(x)\) es la distancia de\(r\) a\(x\) y\(P(x)\) es un camino más corto de\(r\) a\(x\).
- Prueba
-
El teorema sostiene trivialmente cuándo\(x=r\). Entonces consideramos el caso donde\(x \neq r\). Argumentamos que\(δ(x)\) es la distancia de\(r\) a\(x\) y que\(P(x)\) es un camino más corto de\(r\) a\(x\) por inducción en el número mínimo\(k\) de aristas en un camino más corto de\(r\) a\(x\). Cuando\(k=1\), el borde\((r,x)\) es un camino más corto de\(r\) a\(x\). Ya que\(v_1=r\), vamos a establecer\(δ(x)=w(r,x)\) y\(P(x)=(r,x)\) en el Paso 1.
Ahora arregla un entero positivo\(k\). Supongamos que si el número mínimo de aristas en un camino más corto de\(r\) a\(x\) es como máximo\(k\), entonces\(δ(x)\) es la distancia de\(r\) a\(x\) y\(P(x)\) es un camino más corto de\(r\) a\(x\). Let\(x\) Ser un vértice para el cual\(x\) es el número mínimo de aristas en una trayectoria más corta de\(r\) a\(k+1\). Arreglar un camino más corto\(P=(u_0,u_1,u_2,…,u_{k+1})\) de\(r=u_0\) a\(x=u_{k+1}\). Entonces\(Q=(u_0,u_1,…,u_k)\) es un camino más corto de\(r\) a\(u_k\). (Ver Figura 12.19.)
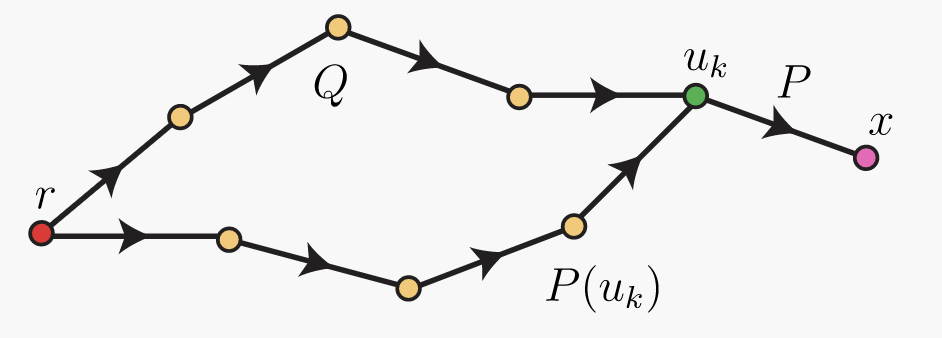
Figura 12.19. Caminos más cortos Por la hipótesis inductiva,\(δ(u_k)\) es la distancia de\(r\) a\(u_k\), y\(P(u_k)\) es un camino más corto de\(r\) a\(u_k\). Tenga en cuenta que no es\(P(u_k)\) necesario que sea lo mismo que path\(Q\), como sugerimos en la Figura 12.19. Sin embargo, si son distintos, los dos caminos tendrán la misma longitud, a saber\(δ(u_k)\). También, la distancia de\(r\) a\(x\) es\(δ(u_k)+w(u_k,x) \geq δ(u_k)\) ya que\(P\) es un camino más corto de\(r\) a\(x\) y\(w(u_k,x)≥0\).
Dejar\(i\) y\(j\) ser los enteros únicos para los cuales\(u_k=v_i\) y\(x=v_j\). Si\(j<i\), entonces
\(δ(x)=δ(v_j)≤δ(v_i)=δ(u_k)≤δ(u_k)+w(u_k)\).
Por lo tanto, el algoritmo ha encontrado una ruta\(P(x)\) de\(r\) a\(x\) tener longitud\(δ(x)\) que es como máximo la distancia de\(r\) a\(x\). Claramente, esto implica que\(δ(x)\) es la distancia de\(r\) a\(x\) y que\(P(x)\) es un camino más corto.
Por otro lado, si\(j>i\), entonces el paso inductivo en Step\(i\) da como resultado
\(δ(x)≤δ(v_i)+w(v_i,y)=δ(u_k)+w(u_k,x)\).
Como antes, esto implica que\(δ(x)\) es la distancia de\(r\) a\(x\) y que\(P(x)\) es un camino más corto.


