12.5: Ejercicios
- Page ID
- 118505
1. Para la gráfica de la Figura 12.20, utilice el algoritmo de Kruskal (“evitar ciclos”) para encontrar un árbol de expansión de peso mínimo. Tu respuesta debe incluir una lista completa de los bordes, indicando qué bordes tomas para tu árbol y cuáles (si los hay) rechazas en el curso de ejecutar el algoritmo.
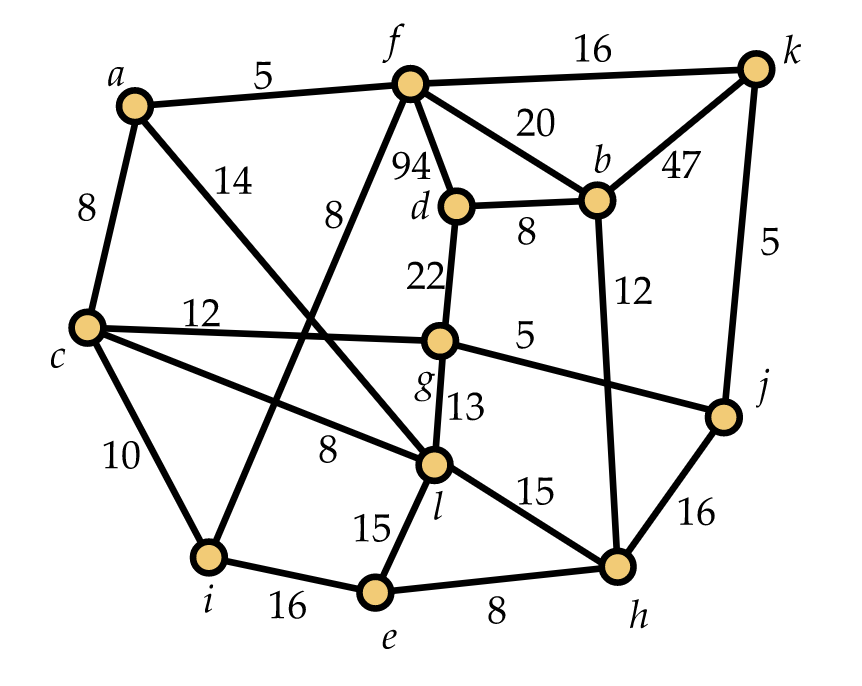
2. Para la gráfica de la Figura 12.20, use el algoritmo de Prim (“build tree”) para encontrar un árbol de expansión de peso mínimo. Su respuesta debe enumerar los bordes seleccionados por el algoritmo en el orden en que fueron seleccionados.
3. Para la gráfica de la Figura 12.21, utilice el algoritmo de Kruskal (“evitar ciclos”) para encontrar un árbol de expansión de peso mínimo. Tu respuesta debe incluir una lista completa de los bordes, indicando qué bordes tomas para tu árbol y cuáles (si los hay) rechazas en el curso de ejecutar el algoritmo.
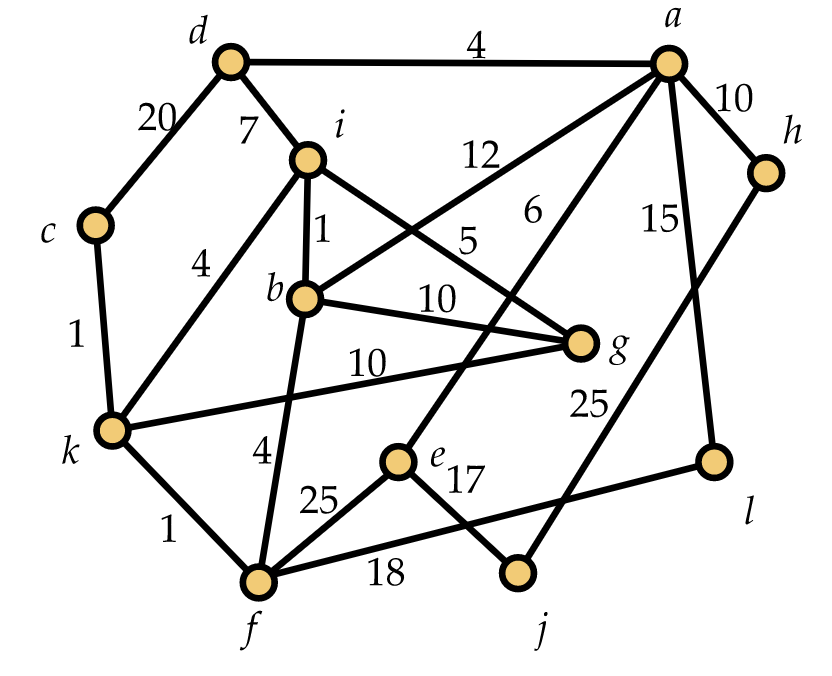
4. Para la gráfica de la Figura 12.21, use el algoritmo de Prim (“build tree”) para encontrar un árbol de expansión de peso mínimo. Su respuesta debe enumerar los bordes seleccionados por el algoritmo en el orden en que fueron seleccionados.
5. Para la gráfica de la Figura 12.22, utilice el algoritmo de Kruskal (“evitar ciclos”) para encontrar un árbol de expansión de peso mínimo. Tu respuesta debe incluir una lista completa de los bordes, indicando qué bordes tomas para tu árbol y cuáles (si los hay) rechazas en el curso de ejecutar el algoritmo.
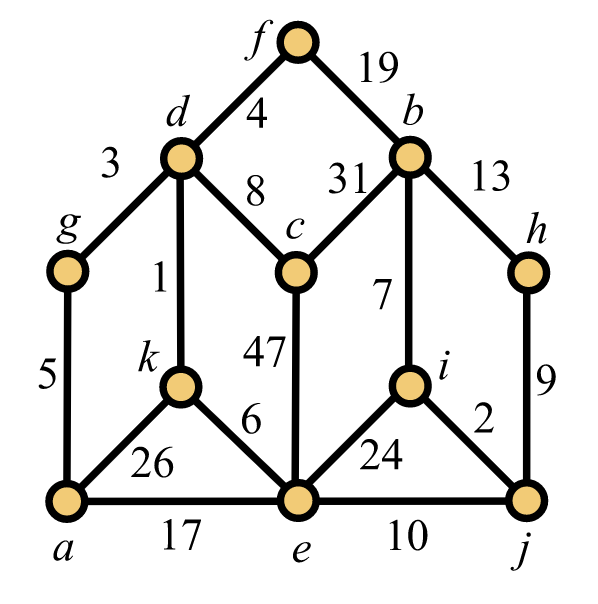
6. Para la gráfica de la Figura 12.22, use el algoritmo de Prim (“build tree”) para encontrar un árbol de expansión de peso mínimo. Su respuesta debe enumerar los bordes seleccionados por el algoritmo en el orden en que fueron seleccionados.
7. Se está creando un nuevo banco local que establecerá una sede\(h\), dos sucursales\(b_1\) y\(b_2\), y cuatro cajeros automáticos\(a_1\)\(a_2\),\(a_3\), y\(a_4\). Necesitan construir una red informática de tal manera que la sede, las sucursales y los cajeros automáticos puedan intercomunicarse. Además, deberán estar en red con el Banco de la Reserva Federal de Atlanta,\(f\). Los costos de las conexiones de red factibles (en unidades de $10,000) se enumeran a continuación:
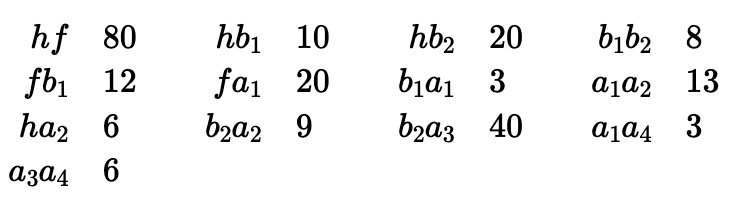
El banco desea minimizar el costo de construir su red (que debe permitir la conexión, posiblemente enrutada a través de otros nodos, de cada nodo a cada otro nodo), sin embargo debido a la necesidad de comunicación de alta velocidad, deben pagar para construir la conexión de\(h\) a \(f\)así como la conexión de\(b_2\) a\(a_3\). Dar una lista de las conexiones que el banco debe establecer para minimizar su costo total, sujeto a esta restricción. Asegúrese de explicar cómo seleccionó las conexiones y cómo sabe que se minimiza el costo total.
8. Un gráfico ponderado desconectado obviamente no tiene árboles de expansión. Sin embargo, es posible encontrar un bosque de expansión de peso mínimo en dicha gráfica. Explicar cómo modificar tanto el algoritmo de Kruskal como el algoritmo de Prim para hacer esto.
9. Demostrar Proposición 12.3.
10. En el artículo donde apareció por primera vez el algoritmo de Kruskal, consideró que el algoritmo era una ruta hacia una mejor prueba de que en una gráfica ponderada conectada sin dos aristas que tuvieran el mismo peso, existe un árbol de expansión de peso mínimo único. Demostrar este hecho usando el algoritmo de Kruskal.
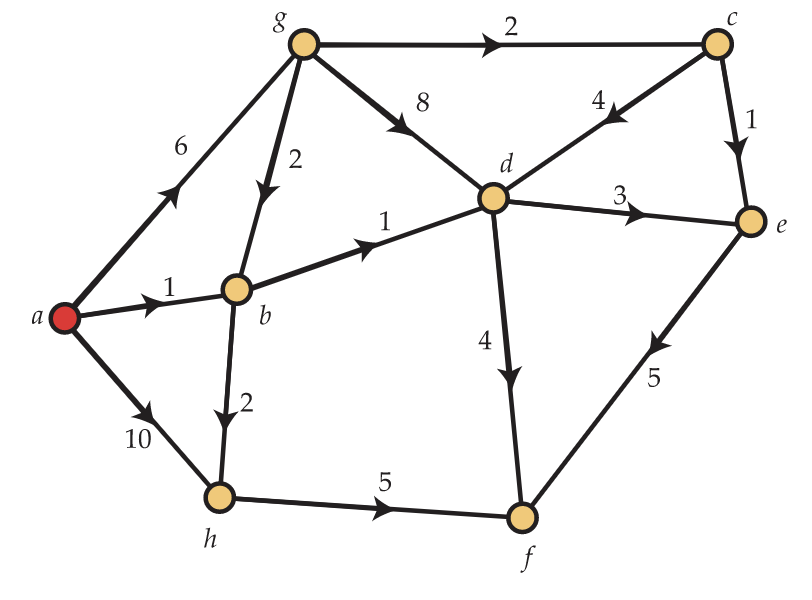
11. Utilice el algoritmo de Dijkstra para encontrar la distancia\(a\) entre vértices en el dígrafo que se muestra en la Figura 12.23 y una trayectoria dirigida de esa longitud.
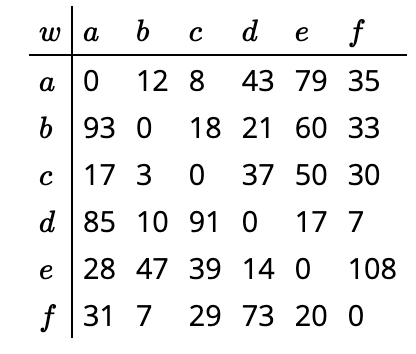
12. La Figura 12.24 contiene la longitud del borde dirigido\((x,y)\) en la intersección de fila\(x\) y columna\(y\) en un dígrafo con vértice establecido\(\{a,b,c,d,e,f\}\). Por ejemplo,\(w(b,d)=21\). (Por otro lado,\(w(d,b)=10\).) Usa estos datos y el algoritmo de Dijkstra para encontrar la distancia\(a\) de cada uno de los otros vértices y una ruta dirigida de esa longitud desde\(a\).
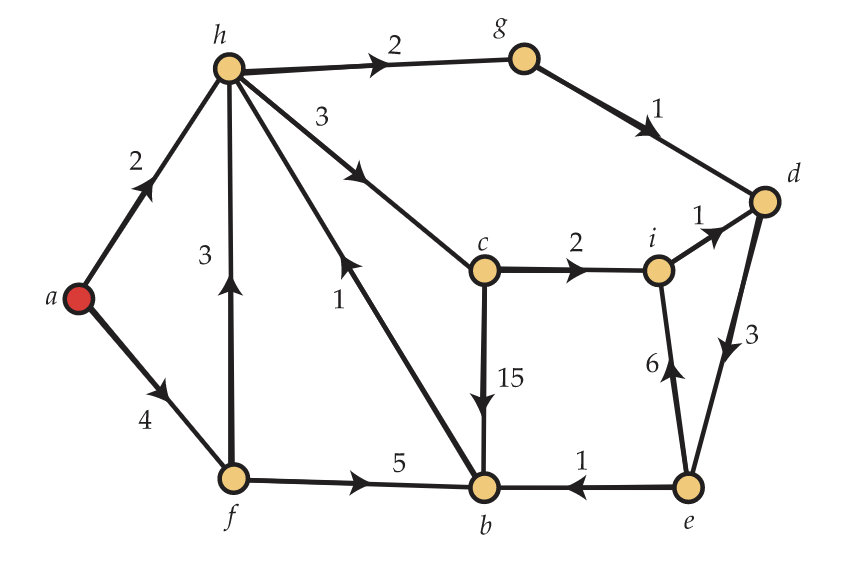
13. Utilice el algoritmo de Dijkstra para encontrar la distancia\(a\) entre vértices en el dígrafo que se muestra en la Figura 12.25 y una trayectoria dirigida de esa longitud.
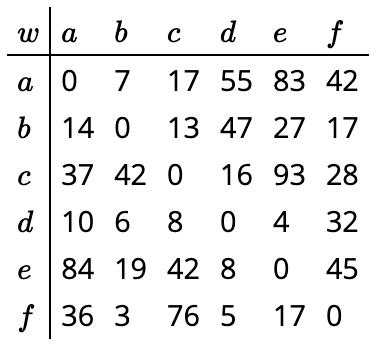
14. La Figura 12.26 contiene la longitud del borde dirigido\((x,y)\) en la intersección de fila\(x\) y columna\(y\) en un dígrafo con vértice establecido\(\{a,b,c,d,e,f\}\). Por ejemplo,\(w(b,d)=47\). (Por otro lado,\(w(d,b)=6\).) Usa estos datos y el algoritmo de Dijkstra para encontrar la distancia\(a\) de cada uno de los otros vértices y una ruta dirigida de esa longitud desde\(a\).
15. Dé un ejemplo de un dígrafo que tiene una ruta no dirigida entre cada par de vértices, pero que tiene un vértice raíz\(r\) para que el algoritmo de Dijkstra no pueda encontrar una ruta de longitud finita desde\(r\) hasta algún vértice\(x\).
16. Observe que en nuestra discusión sobre el algoritmo de Dijkstra, requerimos que los pesos de borde no fueran negativos. Si los pesos de los bordes son longitudes y están destinados a modelar la distancia, esto tiene mucho sentido. Sin embargo, en algunos casos, podría ser razonable permitir pesos de borde negativos. Por ejemplo, supongamos que un peso positivo significa que hay un costo para viajar a lo largo del borde dirigido, mientras que un peso de borde negativo significa que gana dinero para viajar a lo largo del borde dirigido. En este caso, un camino dirigido con peso total positivo da como resultado pagar para recorrerlo, mientras que uno con peso total negativo da como resultado una ganancia.
a. dé un ejemplo para mostrar que el algoritmo de Dijkstra no siempre encuentra la ruta de peso total mínimo cuando se permiten pesos de borde negativos.
b. Bob y Xing están considerando esta situación, y Bob sugiere que una pequeña modificación al algoritmo debería resolver el problema. Dice que si hay pesos negativos, solo tienen que encontrar el más pequeño (es decir, el peso más negativo) y sumar el valor absoluto de ese peso a cada borde dirigido. Por ejemplo, si\(w(x,y)≥−10\) por cada borde dirigido\((x,y)\), Bob está sugiriendo que agreguen 10 a cada peso de borde. Xing es escéptico, y por una buena razón. Da un ejemplo para mostrar por qué la modificación de Bob no va a funcionar.


