13.1: Notación y Terminología Básicas

Última actualización
Guardar como PDF

Page ID: 118261

Mitchel T. Keller & William T. Trotter
Georgia Tech & Morningside College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Una gráfica dirigida en la que por cada par de vértices x, y a lo sumo uno de los bordes dirigidos\((x,y)\) y\((y,x)\) entre ellos está presente se denomina gráfica orientada. La configuración básica para un problema de flujo de red comienza con una gráfica orientada\(G\), llamada red, en la que tenemos dos vértices especiales llamados el origen y el sumidero. Usamos la letra\(S\) para denotar la fuente, mientras que la letra\(T\) se usa para denotar el fregadero (término). Todos los bordes incidentes con la fuente están orientados lejos de la fuente, mientras que todos los bordes incidentes con el fregadero están orientados con el fregadero. Además, en cada borde, tenemos una capacidad no negativa, que funciona como una restricción sobre cuánto se puede transmitir a través del borde. La capacidad del borde\(e=(x,y)\) se denota\(c(e)\) o por\(c(x,y)\). En un programa de computadora, los nodos de una red pueden identificarse con claves enteras, pero en este texto, normalmente usaremos letras para etiquetar los nodos de una red. Esto ayuda a distinguir nodos de capacidades en diagramas de redes. Ilustramos una red en la Figura 13.1. Los números asociados a los bordes son sus capacidades, así, por ejemplo,\(c(E,B)=24\) y\(c(A,T)=56\).

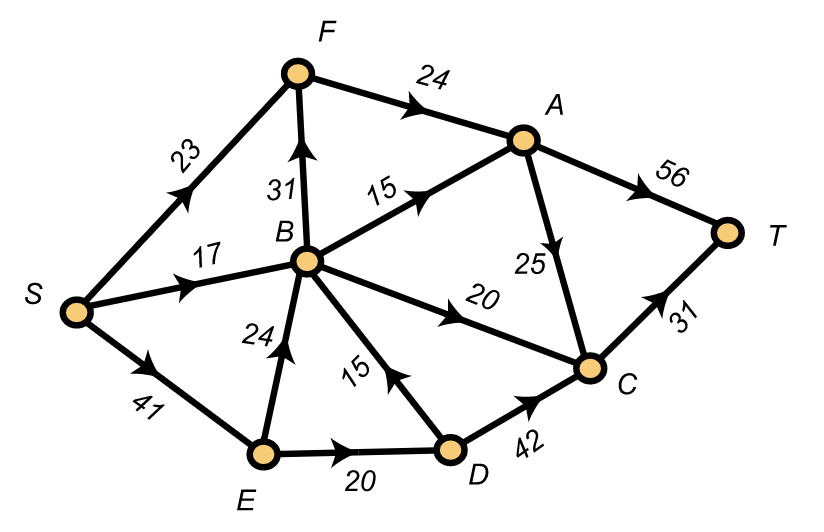
Screen Shot 2022-03-14 a las 10.30.14 PM.png — Figura **13.1.** Una Red

Un flujo\(ϕ\) en una red es una función que asigna a cada borde dirigido\(e=(x,y)\) un valor no negativo\(ϕ(e)=ϕ(x,y)≤c(x,y)\) para que se mantengan las siguientes leyes de conservación:

\(\sum_{x}ϕ(S,x)= \sum_{x}ϕ(x,T)\), es decir, la cantidad que sale de la fuente es igual a la cantidad que llega al fregadero. Esta cantidad se llama el valor del flujo\(ϕ\).
Por cada vértice\(y\) que no es ni la fuente ni el sumidero la cantidad que sale\(y\) es igual a la cantidad ingresada\(y\). Es decir,\(\sum_{x}ϕ(x,y)= \sum_{x}ϕ(y,x)\).

Ilustramos un flujo en una red en la Figura 13.2.

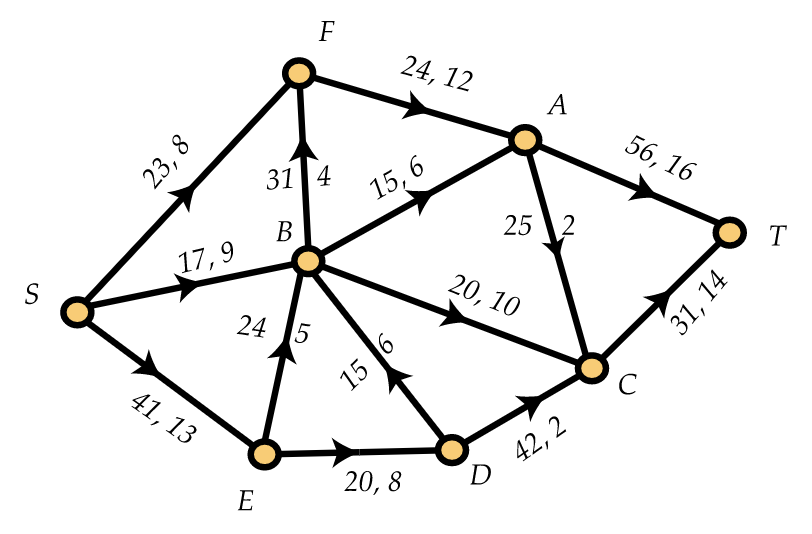
Screen Shot 2022-03-14 a las 10.32.50 PM.png — Figura **13.2.** Un flujo de red

En esta figura, los números asociados a cada borde son su capacidad y la cantidad de flujo que\(ϕ\) coloca en ese borde. Por ejemplo, el borde\((E,D)\) tiene capacidad 20 y actualmente lleva un flujo de 8. (Ya que\(ϕ(x,y)≤c(x,y)\), siempre es fácil determinar qué número es la capacidad y cuál es el flujo.) El valor de este flujo es\(30=ϕ(S,F)+ϕ(S,B)+ϕ(S,E)=ϕ(A,T)+ϕ(C,T)\). Para ver que la segunda ley de conservación se sostiene, por ejemplo, en el vértice\(B\), tenga en cuenta que el flujo de entrada\(B\) es\(ϕ(S,B)+ϕ(E,B)+ϕ(D,B)=20\) y el flujo de salida de\(B\) es\(ϕ(B,F)+ϕ(B,A)+ϕ(B,C)=20\).

Dada una red, es muy fácil encontrar un flujo. Simplemente asignamos\(ϕ(e)=0\) para cada borde\(e\). Es muy fácil subestimar la importancia de esta observación, en realidad. Los problemas de flujo de red son un caso especial de una clase más general de problemas de optimización conocidos como programas lineales, y en general, puede ser muy difícil encontrar una solución factible a un problema de programación lineal. De hecho, conceptualmente, encontrar una solución factible, cualquier solución, es tan difícil como encontrar una solución óptima.