15.1: Colorear los vértices de un cuadrado

Comencemos coloreando los vértices de un cuadrado usando blanco y dorado. Si fijamos la posición del cuadrado en el plano, hay\(2^4=16\) diferentes colorantes. Estos colorantes se muestran en la Figura 15.1.

Figura 15.1. Los 16 colorantes de los vértices de un cuadrado.

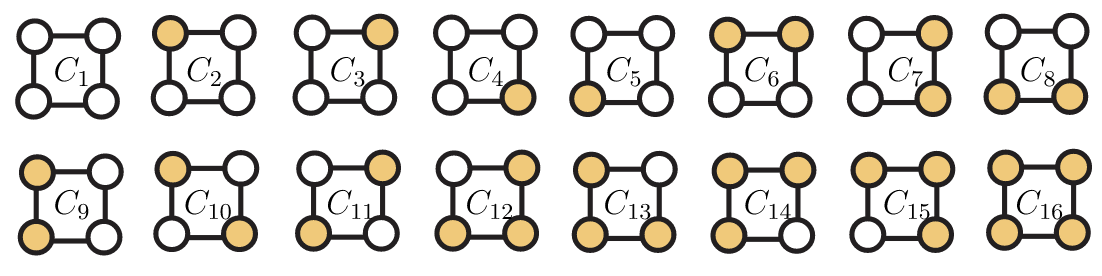
No obstante, si pensamos en el cuadrado como una estructura metálica con una cuenta blanca o una cuenta dorada en cada esquina y permitimos que el marco sea girado y volteado, nos damos cuenta de que muchos de estos colorantes son equivalentes. Por ejemplo, si volteamos coloreando\(C_7\) sobre la línea vertical que divide el cuadrado por la mitad, obtenemos coloración\(C_9\). Si giramos coloreando\(C_2\) en sentido horario por\(90^\circ\), obtenemos coloración\(C_3\). En muchos casos, queremos considerar tales colorantes equivalentes como un solo colorante. (Recordemos nuestro motivador ejemplo de collares hechos de cuentas de colores. Tiene poco sentido diferenciar entre dos collares si uno puede ser girado y volteado para convertirse en el otro.)

Para determinar sistemáticamente cuántos de los colorantes mostrados en la Figura 15.1 no son equivalentes, debemos pensar en las transformaciones que podemos aplicar al cuadrado y qué hace cada uno a los colorantes. Antes de examinar los efectos de las transformaciones en los colorantes, tomemos un momento para ver cómo reordenan los vértices. Para ello, consideramos que el vértice superior izquierdo es 1, el vértice superior derecho es 2, el vértice inferior derecho es 3 y el vértice inferior izquierdo es 4. Denotamos la rotación en sentido horario por\(90^\circ\) por\(r_1\) y vemos que\(r_1\) envía el vértice en la posición 1 a la posición 2, el vértice en la posición 2 a la posición 3, el vértice en la posición 3 a la posición 4, y el vértice en la posición 4 a la posición 1. Por brevedad, escribiremos\(r1(1)=2, r1(2)=3\), etc. también podemos rotar el cuadrado en sentido horario\(180^\circ\) y denotar esa rotación por\(r_2\). En este caso, nos encontramos con eso\(r2(1)=3, r2(2)=4, r2(3)=1\), y\(r2(4)=2\). Observe que podemos lograr la transformación\(r_2\) haciendo\(r_1\) dos veces seguidas. Además, la rotación en sentido horario por\(270^\circ]), \(r_3\), se puede lograr haciendo\(r_1\) tres veces seguidas. (Las rotaciones en sentido antihorario se pueden evitar al señalar que tienen el mismo efecto que una rotación en sentido horario, aunque con un ángulo diferente).

Cuando se trata de voltear el cuadrado, hay cuatro ejes sobre los que podemos voltearlo: vertical, horizontal, diagonal de pendiente positiva y diagonal de pendiente negativa. Denotamos estos volteos por\(v, h, p\), y\(n\), respectivamente. Ahora fíjate en eso\(v(1)=2, v(2)=1, v(3)=4\), y\(v(4)=3\). Para el volteo alrededor del eje horizontal, tenemos\(h(1)=4, h(2)=3, h(3)=2\), y\(h(4)=1\). Para\(p\), tenemos\(p(1)=3, p(2)=2, p(3)=1\), y\(p(4)=4\). Por último, para\(n\) que nos encontremos\(n(1)=1, n(2)=4, n(3)=3\), y\(n(4)=2\). Hay una transformación más que debemos mencionar; la transformación que no le hace nada a la plaza se llama transformación de identidad, denotada\(ι\). Tiene\(ι(1)=1, ι(2)=2, ι(3)=3\), y\(ι(4)=4\).

Ahora que hemos identificado las ocho transformaciones del cuadrado, hagamos una tabla que muestre qué colorantes de la Figura 15.1 quedan inalterados por la aplicación de cada transformación. No es sorprendente que la transformación de la identidad deje sin cambios todos los colorantes. Debido a que\(r_1\) mueve los vértices cíclicamente, vemos que sólo\(C_1\) y\(C_{16}\) permanecen sin cambios cuando se aplica. Cualquier coloración con más de un color tendría un vértice de un color movido a uno del otro color. Consideremos por qué colorantes se fijan\(v\), el volteo alrededor del eje vertical. Para que esto suceda, el color en la posición 1 debe ser el mismo que el color en la posición 2, y el color en la posición 3 debe ser el mismo que el color en la posición 4. Así, esperaríamos encontrar\(2 \cdot 2=4\) colorantes sin cambios por\(v\). Examinando la Figura 15.1, vemos que estos colorantes son\(C_1, C_6, C_8\), y\(C_{16}\). Realizar un análisis similar para las cinco transformaciones restantes conduce a la Figura 15.2.

Figura 15.2. Colorantes fijados por transformaciones del cuadrado

En este punto, es natural preguntar a dónde va esto. Después de todo, estamos tratando de contar el número de colorantes no equivalentes, y la Figura 15.2 no hace ningún esfuerzo por agrupar los colorantes en función de cómo una transformación cambia una coloración a otra. Resulta que existe una conexión útil entre contar los colorantes no equivalentes y determinar el número de colorantes fijados por cada transformación. Para desarrollar esta conexión, primero necesitamos discutir la relación de equivalencia creada por la acción de las transformaciones del cuadrado en el conjunto\(\mathcal{C}\) de todos los 2 colores del cuadrado. (Remítase a la Sección B.13 para un repaso sobre la definición de relación de equivalencia.) Para ello, observe que aplicar una transformación a un cuadrado con vértices coloreados da como resultado otro cuadrado con vértices coloreados. Por ejemplo, aplicar la transformación\(r_1\) a un cuadrado coloreado como en\(C_{12}\) da como resultado un cuadrado coloreado como en\(C_{13}\). Decimos que las transformaciones del cuadrado actúan sobre el conjunto\(\mathcal{C}\) de colorantes. Denotamos esta acción añadiendo una estrella al nombre de transformación. Por ejemplo,\(r_1^∗(C_{12})=C_{13}\) y\(v^∗(C_{10})=C_{11}\).

Si\(τ\) es una transformación del cuadrado con\(τ^∗(C_i)=C_j\), entonces decimos coloraciones\(C_i\) y\(C_j\) son equivalentes y escribimos\(C_i~C_j\). Ya que\(ι^∗(C)=C\) para todos\(C∈ \mathcal{C}\), ~ es reflexivo. Si\(τ_1^∗(C_i)=C_j\) y\(τ_2^∗(C_j)=C_k\), entonces\(τ_2^∗(τ_1^∗(C_i))=C_k\), entonces ~ es transitivo. Para completar nuestra verificación de que ∼ es una relación de equivalencia, debemos establecer que es simétrica. Para ello, requerimos de la noción de lo inverso de una transformación\(τ\), que es simplemente la transformación τ−1 que deshace lo que haya\(τ\) hecho. Por ejemplo, la inversa de\(r_1\) es la rotación en sentido contrario a las agujas del reloj por\(90^\circ\), que tiene el mismo efecto en la ubicación de los vértices que\(r_3\). Si\(τ^∗(C_i)=C_j\), entonces\(τ^{−1∗}(C_j)=C_i\), entonces ~ es simétrico.

Antes de proceder a establecer la conexión entre el número de colorantes no equivalentes (clases de equivalencia bajo ~) y el número de colorantes fijados por una transformación en plena generalidad, veamos cómo se ve para nuestro ejemplo. Al mirar la Figura 15.1, debe notar que ~\(\mathcal{C}\) divide en seis clases de equivalencia. Dos contienen una coloración cada una (todas las coloraciones blancas y todas doradas). Uno contiene dos colorantes (\(C_{10}\)y\(C_{11}\)). Finalmente, tres contienen cuatro colorantes cada uno (un vértice dorado, un vértice blanco y los cuatro restantes con dos vértices de cada color). Ahora mira de nuevo a la Figura 15.2 y suma el número de colorantes fijados por cada transformación. Al hacer esto, obtenemos 48, y cuando 48 se divide por el número de transformaciones (8), ¡obtenemos 6 (el número de clases de equivalencia)! Resulta que esto está lejos de ser una casualidad, como pronto veremos. Primero, sin embargo, introducimos el concepto de grupo de permutación para generalizar nuestro conjunto de transformaciones de la plaza.