15.6: Ejercicios

Última actualización
Guardar como PDF

Page ID: 118326

Mitchel T. Keller & William T. Trotter
Georgia Tech & Morningside College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1. Escribe las permutaciones que se muestran a continuación en notación de ciclo.

\ begin {pmatrix}

1 y 2 y 3 y 4 y 5 y 6\\

4 y 2 y 5 y 6 y 3 y 1

\ end {pmatrix}

2. Cómputos$\pi_1 \pi_2, \pi_2 \pi_1, \pi_3 \pi_4$, y$\pi_4 \pi_3$ para las permutaciones$\pi_i$ en el Ejercicio 15.6.1.

3. Encuentre$stab_{D_8}⁡(C_3)$ y$stab_{D_8}⁡(C_{16})$ para las coloraciones de los vértices del cuadrado que se muestra en la Figura 15.1 haciendo referencia a la Figura 15.2.

4. En la Figura 15.15, se muestra un pentágono regular con sus vértices etiquetados. Use este etiquetado para completar este ejercicio.

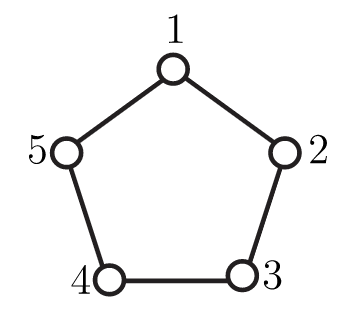
$Screen Shot 2022-03-20 en 5.04.02 PM.png$

Figura 15.15. Un pentágono con vértices etiquetados

a. El grupo diedro del pentágono,$D_{10}$, contiene 10 permutaciones. Dejar$r_1=(12345)$ ser la rotación en sentido horario por$72^\circ $ y$f_1=(1)(25)(34)$ ser el volteo alrededor de la línea que pasa por 1 y perpendicular al lado opuesto. Dejemos$r_2, r_3$, y$r_4$ sean las otras rotaciones adentro$D_{10}$. Denote el volteo alrededor de la línea que pasa por el vértice$i$ y perpendicular al otro lado por$f_i$,$1≤i≤5$. Escribe todos los 10 elementos de$D_{10}$ en notación de ciclo.

b. Supongamos que estamos coloreando los vértices del pentágono usando blanco y negro. Dibuja los colorantes fijados por$r_1$. Dibuja los colorantes fijados por$f_1$.

c. Encuentra$stab_{D_{10}}⁡(C)$ dónde$C$ está la coloración de los vértices del pentágono en los que los vértices 1, 2 y 5 son de color negro y los vértices 3 y 4 son de color blanco.

d. encontrar el índice de ciclo de$D_{10}$.

e. utilizar el índice de ciclo para determinar el número de colorantes no equivalentes de vértices del pentágono usando blanco y negro.

f. haciendo una sustitución apropiada para el índice$x_i$ en el ciclo, encontrar el número de colorantes no equivalentes de los vértices del pentágono en los que dos vértices son coloreados de negro y tres vértices son de color blanco. Dibuja estos colorantes.

5. Escribe todas las permutaciones en$C_{12}$, el grupo cíclico de orden 12, en notación de ciclo.

6. La escala occidental de 12 notas no es el único sistema en el que se basa la música. En la música clásica tailandesa se utiliza una escala con siete notas equiespaciadas por octava. Al igual que en la música occidental, una escala es un subconjunto de estas siete notas, y dos escalas son equivalentes si son transposiciones entre sí. Encuentra el número de escalas$k$ de notas en la música clásica tailandesa para$1 \leq k \leq 7$.

7. El xileno es un hidrocarburo aromático que tiene dos grupos metilo (y cuatro átomos de hidrógeno) unidos al anillo de carbono hexagonal. ¿Cuántos isómeros hay del xileno?

8. Encuentra las permutaciones en$S_4^{(2)}$ correspondientes a las permutaciones (1234) y (12) (34) en$S_4$. Confirmar que el primero consiste en un ciclo de 4 y uno de 2 ciclos y el segundo consta de dos ciclos de 2 y dos de 1 ciclo.

9. Dibuja las tres gráficas no isomórficas en cuatro vértices con 3 aristas y las dos gráficas no isomórficas en cuatro vértices con 4 aristas.

10.

a. Utilice el método de la Subsección 15.5.3 para encontrar el índice de ciclo del grupo$S_5^{(2)}$ de pares del grupo simétrico sobre cinco elementos.

b. utilizar el índice de ciclo del ítem 15.6.10.a para determinar el número de gráficas no isomórficas en cinco vértices. ¿Cuántos de ellos tienen 6 bordes?

11. Tic-tac-toe es un juego para dos jugadores que se juega en una grilla de 9×9. Los jugadores marcan los cuadrados de la cuadrícula con los símbolos X y O. Este ejercicio utiliza el teorema de enumeración de Pólya para investigar el número de diferentes tablas tic-tac-toe. (El análisis de los juegos es más complejo, ya que requiere atención al orden en que se marcan los cuadrados y detenerse cuando un jugador ha ganado el juego).

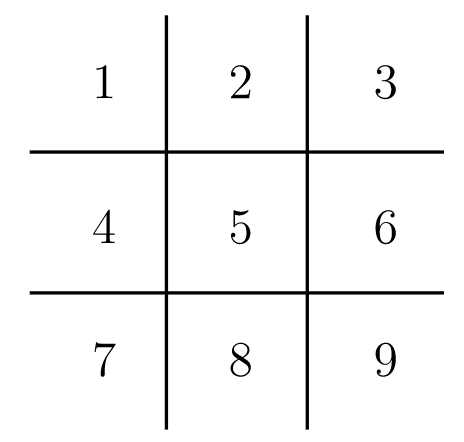
$Screen Shot 2022-03-20 a las 5.11.23 PM.png$

Figura 15.16. Cuadrados numerados de una tabla tic-tac-toe

a. Dos tablas tic-tac-toe son equivalentes si una puede obtenerse de la otra girando la placa o volteándola. (Imagínese que está dibujado sobre una pieza transparente de plástico.) Dado que la cuadrícula 9×9 es un cuadrado, el grupo que actúa sobre ella de esta manera es el grupo diedro$D_8$ que hemos estudiado en este capítulo. Sin embargo, al igual que con el conteo de gráficas no isomórficas, tenemos que tener cuidado para elegir la forma en que se representa este grupo en términos de ciclos. Aquí nos interesa cómo las permutaciones reordenan los nueve cuadrados del tablero tic-tac-toe numerados en la Figura 15.16. Por ejemplo, el efecto de la transformación$r_1$, que gira el tablero en$90^\circ$ sentido horario, puede representarse como una permutación de los nueve cuadrados como (13971) (2684) (5).

Escribe cada uno de los ocho elementos de$D_8$ como permutaciones de los nueve cuadrados de una tabla tic-tac-toe.

b. Encontrar el índice de ciclo de$D_8$ en términos de estas permutaciones.

c. Hacer una sustitución apropiada para$x_i$ en el índice de ciclo para encontrar una función generadora$t(X,O)$ en la que el coeficiente on$X^iO^j$ es el número de tablas tic-tac-toe no equivalentes que tienen$i$ cuadrados rellenos por el símbolo X y$j$ cuadrados rellenos por el símbolo O. (Observe que algunos ¡los cuadrados podrían estar en blanco!)

d. ¿Cuántas tablas tic-tac-toe no equivalentes hay?

e. ¿Cuántas tablas tic-tac-toe no equivalentes tienen tres X y tres O?

f. al jugar tic-tac-toe, los jugadores alternan turnos, cada uno dibujando su símbolo en una sola casilla desocupada durante un turno. Asumiendo que el primer jugador marca sus casillas con X y el segundo marca la suya con O, entonces en cada etapa del juego hay o bien el mismo número de X's y O's o una X más que O's. Usa este hecho y$t(X,O)$ para determinar el número de tablas tic-tac-toe no equivalentes que realmente se pueden obtener al jugar un juego, suponiendo que los jugadores continúen hasta que el tablero esté lleno, independientemente de que uno de ellos haya ganado el juego.

12. Supongamos que está pintando las caras de un cubo y tiene pintura blanca, dorada y azul disponible. Dos cubos pintados son equivalentes si puedes rotar uno de ellos para que todas las caras correspondientes estén pintadas del mismo color. Determine el número de formas no equivalentes en las que puede pintar las caras del cubo así como el número que tiene dos caras de cada color.

Insinuación: Puede ser útil etiquetar las caras como U (“arriba”), D (“abajo”), F (“frente”), B (“atrás”), L (“izquierda”) y R (“derecha”) en lugar de usar números enteros. Trabajar con un modelo tridimensional de un cubo también ayudará a identificar las permutaciones que necesita.