1.2: Ejemplos
- Page ID
- 117123
Supongamos que tenemos un tablero de ajedrez, y una colección de fichas, como dominó, cada una de las cuales es del tamaño de dos cuadrados en el tablero de ajedrez. ¿El tablero de ajedrez puede ser cubierto por los dominó? Primero tenemos que ser claros sobre las reglas: el tablero está cubierto si los dominó están dispuestos de manera que cada uno cubra exactamente dos cuadrados del tablero; no se superponen dominó; y cada cuadrado está cubierto. La respuesta es fácil: simplemente colocando 32 fichas de dominó en filas, la tabla puede cubrirse. Para que el problema sea más interesante, permitimos que el tablero sea rectangular de cualquier tamaño, y permitimos que se retiren algunos cuadrados del tablero. ¿Qué se puede decir sobre si se puede cubrir el tablero restante? Esta es una placa de este tipo, por ejemplo:
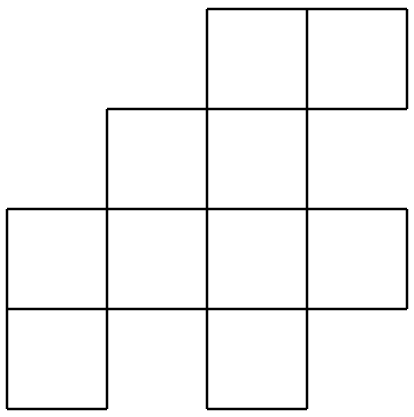
¿Qué podemos decir? Aquí hay una observación fácil: cada dominó debe cubrir dos cuadrados, por lo que el número total de cuadrados debe ser par; el tablero de arriba tiene un número par de cuadrados. ¿Eso es suficiente? No es demasiado difícil convencerse de que esta junta no puede ser cubierta; ¿hay algún principio general en funcionamiento? Supongamos que redibujamos el tablero para enfatizar que realmente es parte de un tablero de ajedrez:
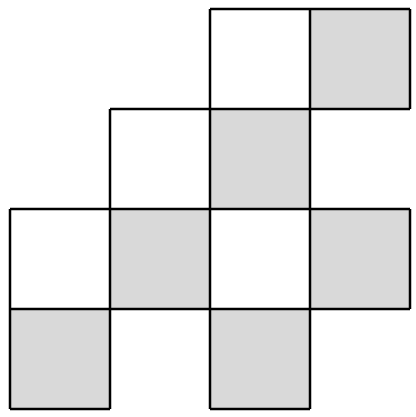
¡Ajá! Cada baldosa debe cubrir un cuadrado blanco y otro gris, pero hay cuatro de los primeros y seis de los segundos, por lo que es imposible. Ahora tenemos el cuadro completo? No; por ejemplo:
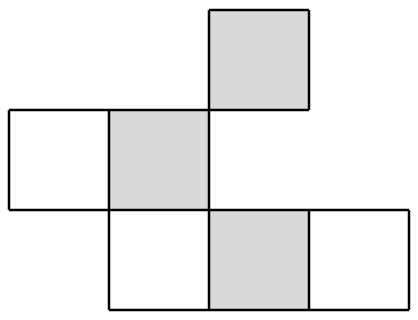
El cuadrado gris en la parte superior derecha claramente no puede cubrirse. Desafortunadamente no es fácil afirmar una condición que caracterice completamente a las tablas que se pueden cubrir; volveremos a ver este problema. Notemos, sin embargo, que este problema también puede representarse como un problema gráfico. Introducimos un vértice correspondiente a cada cuadrado, y conectamos dos vértices por un borde si sus cuadrados asociados pueden ser cubiertos por un solo dominó; aquí está el tablero anterior:
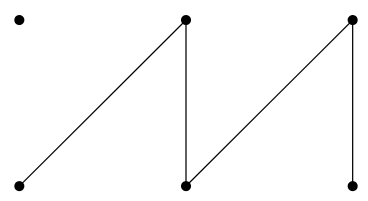
Aquí la fila superior de vértices representa los cuadrados grises, la fila inferior los cuadrados blancos. Un dominó corresponde ahora a un borde; una cubierta por dominó corresponde a una colección de aristas que no comparten puntos finales y que son incidentes con (es decir, tocan) los seis vértices. Dado que ningún borde incide con el vértice superior izquierdo, no hay cobertura.
Quizás el problema más famoso de la teoría gráfica se refiere a la coloración de mapas: Dado un mapa de algunos países, ¿cuántos colores se requieren para colorear el mapa para que los países que comparten una frontera obtengan colores diferentes? Durante mucho tiempo se conjeturó que cualquier mapa podía ser coloreado con cuatro colores, y esto finalmente se probó en 1976. Aquí hay un ejemplo de un pequeño mapa, coloreado con cuatro colores:
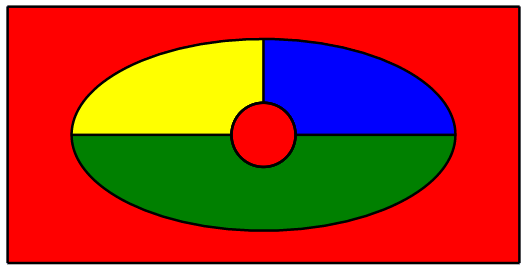
Typically this problem is turned into a graph theory problem. Suppose we add to each country a capital, and connect capitals across common boundaries. Coloring the capitals so that no two connected capitals share a color is clearly the same problem. For the previous map:
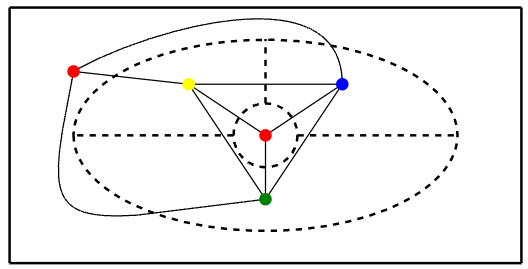
Any graph produced in this way will have an important property: it can be drawn so that no edges cross each other; this is a planar graph. Non-planar graphs can require more than four colors, for example this graph:
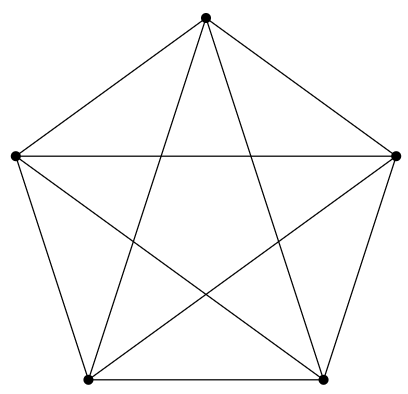
This is called the complete graph on five vertices, denoted \(K_5\); in a complete graph, each vertex is connected to each of the others. Here only the "fat'' dots represent vertices; intersections of edges at other points are not vertices. A few minutes spent trying should convince you that this graph cannot be drawn so that its edges don't cross, though the number of edge crossings can be reduced.


