5.3: Ciclos y caminos de Hamilton
- Page ID
- 117094
Aquí hay un problema similar al problema de los puentes Königsberg: supongamos que varias ciudades están conectadas por una red de carreteras. ¿Es posible visitar todas las ciudades exactamente una vez, sin recorrer ninguna carretera dos veces? Suponemos que estos caminos no se cruzan excepto en las ciudades. Nuevamente hay dos versiones de este problema, dependiendo de si queremos terminar en la misma ciudad en la que empezamos.
Este problema puede ser representado por una gráfica: los vértices representan ciudades, los bordes representan las carreteras. Queremos saber si esta gráfica tiene un ciclo, o camino, que usa cada vértice exactamente una vez. (Recordemos que un ciclo en una gráfica es un subgrafo que es un ciclo, y un camino es un subgrafo que es un camino.) No hay beneficio ni inconveniente en los bucles y múltiples aristas en este contexto: los bucles nunca se pueden usar en un ciclo o trayectoria de Hamilton (excepto en el caso trivial de una gráfica con un solo vértice), y como máximo se puede usar uno de los bordes entre dos vértices. Entonces asumimos para esta discusión que todas las gráficas son simples.
Definición\(\PageIndex{1}\): Hamilton path
Un ciclo que usa cada vértice en una gráfica exactamente una vez se llama ciclo Hamilton, y un camino que usa cada vértice en una gráfica exactamente una vez se llama camino de Hamilton.
Desafortunadamente, este problema es mucho más difícil que los correspondientes problemas de circuito y caminata de Euler; no hay una buena caracterización de gráficas con caminos y ciclos de Hamilton. Tenga en cuenta que si una gráfica tiene un ciclo Hamilton entonces también tiene un camino Hamilton.
Existen algunas condiciones útiles que implican la existencia de un ciclo o camino Hamilton, que suelen decir de alguna forma que hay muchos bordes en la gráfica. Un ejemplo extremo es la gráfica completa\(K_n\): tiene tantos bordes como cualquier gráfica simple en\(n\) vértices puede tener, y tiene muchos ciclos Hamilton. El problema para una caracterización es que hay gráficas con ciclos Hamilton que no tienen muchos bordes. El más simple es un ciclo,\(C_n\): esto solo tiene\(n\) bordes pero tiene un ciclo Hamilton. Por otro lado, la Figura\(\PageIndex{1}\) muestra gráficas con apenas unos pocos bordes más que el ciclo en el mismo número de vértices, pero sin ciclos Hamilton.

También hay gráficas que parecen tener muchos bordes, sin embargo no tienen ciclo Hamilton, como se indica en la Figura\(\PageIndex{2}\).
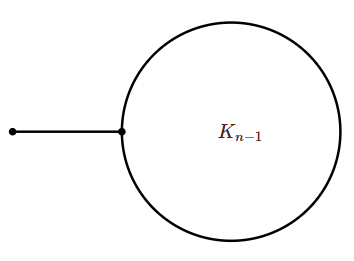
La clave para una condición exitosa suficiente para garantizar la existencia de un ciclo Hamilton es requerir muchos bordes en muchos vértices.
Teorema \(\PageIndex{1}\)
Si\(G\) es una gráfica simple sobre\(n\) vértices,\(n\ge3\), y\(\text{d}(v)+\text{d}(w)\ge n\) siempre\(v\) y no\(w\) son adyacentes, entonces\(G\) tiene un ciclo Hamilton.
- Prueba
-
Primero mostramos que\(G\) está conectado. Si no, dejar\(v\) y\(w\) ser vértices en dos componentes conectados diferentes de\(G\), y supongamos que los componentes tienen\(n_1\) y\(n_2\) vértices. Entonces\(\text{d}(v)\le n_1-1\) y\(\text{d}(w)\le n_2-1\), entonces\(\text{d}(v)+\text{d}(w)\le n_1+n_2-2< n\). Pero como\(v\) y no\(w\) son adyacentes, esto es una contradicción.
Ahora considere un camino más largo posible en\(G\):\(v_1,v_2,\ldots,v_k\). Supongamos, para una contradicción\(k< n\), que, entonces hay algún vértice\(w\) adyacente a uno de\(v_2,v_3,\ldots,v_{k-1}\), digamos a\(v_i\). Si\(v_1\) es adyacente a\(v_k\), entonces\(w,v_i,v_{i+1},\ldots,v_k,v_1,v_2,\ldots v_{i-1}\) es un camino de longitud\(k+1\), una contradicción. De ahí, no\(v_1\) es adyacente a\(v_k\), y así\(\text{d}(v_1)+\text{d}(v_k)\ge n\). Los vecinos de\(v_1\) están entre\(\{v_2,v_3,\ldots,v_{k-1}\}\) como están los vecinos de\(v_k\). Consideremos los vértices\[W=\{v_{l+1}\mid v_{l} \hbox{ is a neighbor of \(v_k\)}\}.\nonumber\] Entonces\(|N(v_k)|=|W|\)\(W\subseteq \{v_3,v_4,\ldots,v_k\}\) y y\(N(v_1)\subseteq \{v_2,v_3,\ldots,v_{k-1}\}\), entonces\(W\cup N(v_1)\subseteq \{v_2,v_3,\ldots,v_{k}\}\), un conjunto con\(k-1< n\) elementos. Ya que\(|N(v_1)|+|W|=|N(v_1)|+|N(v_k)|\ge n\),\(N(v_1)\) y\(W\) debe tener un elemento común,\(v_j\); tenga en cuenta que\(3\le j\le k-1\). Entonces este es un ciclo de longitud\(k\):\[v_1,v_j,v_{j+1},\ldots,v_k,v_{j-1},v_{j-2},\ldots,v_1.\nonumber\] Podemos remarcar los vértices por conveniencia:\[v_1=w_1,w_2,\ldots,w_k=v_2,w_1.\nonumber\] Ahora como antes,\(w\) es adyacente a algunos\(w_l\), y\(w,w_l,w_{l+1},\ldots,w_k,w_1,w_2,\ldots w_{l-1}\) es un camino de longitud\(k+1\), una contradicción. Así\(k=n\), y, renumerando los vértices para mayor comodidad, tenemos un camino Hamilton\(v_1,v_2,\ldots,v_n\). Si\(v_1\) es adyacente a\(v_n\), hay un ciclo Hamilton, según se desee.
Si no\(v_1\) es adyacente a\(v_n\), los vecinos de\(v_1\) se encuentran entre\(\{v_2,v_3,\ldots,v_{n-1}\}\) como están los vecinos de\(v_n\). Consideremos los vértices\[W=\{v_{l+1}\mid v_l \hbox{ is a neighbor of \(v_n\)}\}.\nonumber\] Entonces\(|N(v_n)|=|W|\) y\(W\subseteq \{v_3,v_4,\ldots,v_n\}\), y\(N(v_1)\subseteq \{v_2,v_3,\ldots,v_{n-1}\}\), entonces\(W\cup N(v_1)\subseteq \{v_2,v_3,\ldots,v_{n}\}\), un conjunto con\(n-1< n\) elementos. Ya que\(|N(v_1)|+|W|=|N(v_1)|+|N(v_k)|\ge n\),\(N(v_1)\) y\(W\) debe tener un elemento común,\(v_i\); tenga en cuenta que\(3\le i\le n-1\). Entonces este es un ciclo de duración\(n\):\[v_1,v_i,v_{i+1},\ldots,v_k,v_{i-1},v_{i-2},\ldots,v_1,\nonumber\] y es un ciclo de Hamilton.
La propiedad utilizada en este teorema se llama la propiedad Mineral; si una gráfica tiene la propiedad Mineral también tiene un camino Hamilton, pero podemos debilitar ligeramente la condición si nuestro objetivo es mostrar que hay un camino Hamilton. La prueba de este teorema es casi idéntica a la prueba anterior.
Teorema \(\PageIndex{2}\)
Si\(G\) es una gráfica simple sobre\(n\) vértices y\(\text{d}(v)+\text{d}(w)\ge n-1\) siempre\(v\) y no\(w\) son adyacentes, entonces\(G\) tiene un camino Hamilton.
Supongamos que no\(G\) es sencillo. La existencia de múltiples aristas y bucles no puede ayudar a producir un ciclo de Hamilton cuando\(n\geq 3\): si usamos un segundo borde entre dos vértices, o usamos un bucle, hemos repetido un vértice. Para extender el teorema del mineral a los multígrafos, consideramos la condensación de\(G\): Cuando\(n≥3\), la condensación de\(G\) es simple, y tiene un ciclo de Hamilton si y solo si\(G\) tiene un ciclo Hamilton. Entonces, si la condensación de\(G\) satisface la propiedad Mineral, entonces\(G\) tiene un ciclo Hamilton.


