5.2: Euler Circuitos y Paseos
- Page ID
- 117098
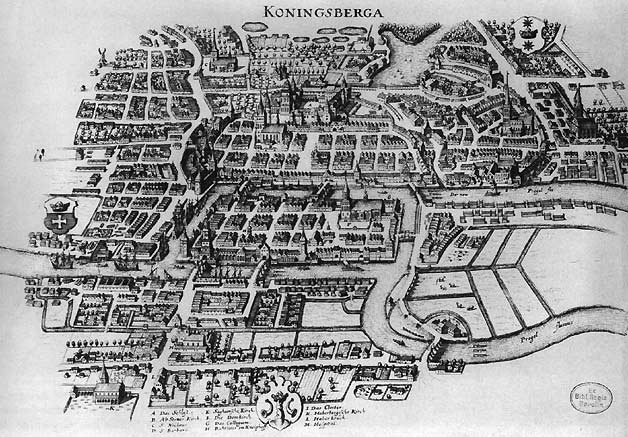
El primer problema en la teoría gráfica data de 1735, y se llama los Siete Puentes de Königsberg. En Königsberg había dos islas, conectadas entre sí y con el continente por siete puentes, como se muestra en la Figura\(\PageIndex{1}\). La pregunta, que llegó a Euler, era si era posible dar un paseo y cruzar cada puente exactamente una vez; Euler demostró que no es posible.
Podemos representar este problema como una gráfica, como en la Figura\(\PageIndex{2}\).
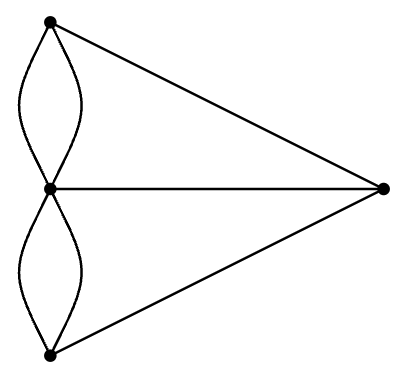
Los dos lados del río están representados por los vértices superior e inferior, y las islas por los dos vértices medios. Hay dos posibles interpretaciones de la pregunta, dependiendo de si el objetivo es terminar la caminata en su punto de partida. Quizás inspirado por este problema, un paseo en una gráfica se define de la siguiente manera.
Definition \(\PageIndex{1}\): Closed Walk or a Circuit
A walk in a graph is a sequence of vertices and edges, \[v_1,e_1,v_2,e_2,\ldots,v_k,e_k,v_{k+1}\nonumber\] such that the endpoints of edge \(e_i\) are \(v_i\) and \(v_{i+1}\). In general, the edges and vertices may appear in the sequence more than once. If \(v_1=v_{k+1}\), the walk is a closed walk or a circuit.
We will deal first with the case in which the walk is to start and end at the same place. A successful walk in Königsberg corresponds to a closed walk in the graph in which every edge is used exactly once.
What can we say about this walk in the graph, or indeed a closed walk in any graph that uses every edge exactly once? Such a walk is called an Euler circuit. If there are no vertices of degree 0, the graph must be connected, as this one is. Beyond that, imagine tracing out the vertices and edges of the walk on the graph. At every vertex other than the common starting and ending point, we come into the vertex along one edge and go out along another; this can happen more than once, but since we cannot use edges more than once, the number of edges incident at such a vertex must be even. Already we see that we're in trouble in this particular graph, but let's continue the analysis. The common starting and ending point may be visited more than once; except for the very first time we leave the starting vertex, and the last time we arrive at the vertex, each such visit uses exactly two edges. Together with the edges used first and last, this means that the starting vertex must also have even degree. Thus, since the Königsberg Bridges graph has odd degrees, the desired walk does not exist.
The question that should immediately spring to mind is this: if a graph is connected and the degree of every vertex is even, is there an Euler circuit? The answer is yes.
If \(G\) is a connected graph, then \(G\) contains an Euler circuit if and only if every vertex has even degree.
- Proof
-
We have already shown that if there is an Euler circuit, all degrees are even.
We prove the other direction by induction on the number of edges. If \(G\) has no edges the problem is trivial, so we assume that \(G\) has edges.
We start by finding some closed walk that does not use any edge more than once: Start at any vertex \(v_0\); follow any edge from this vertex, and continue to do this at each new vertex, that is, upon reaching a vertex, choose some unused edge leading to another vertex. Since every vertex has even degree, it is always possible to leave a vertex at which we arrive, until we return to the starting vertex, and every edge incident with the starting vertex has been used. The sequence of vertices and edges formed in this way is a closed walk; if it uses every edge, we are done.
Otherwise, form graph \(G'\) by removing all the edges of the walk. \(G'\) is not connected, since vertex \(v_0\) is not incident with any remaining edge. The rest of the graph, that is, \(G'\) without \(v_0\), may or may not be connected. It consists of one or more connected subgraphs, each with fewer edges than \(G\); call these graphs \(G_1\), \(G_2\),…,\(G_k\). Note that when we remove the edges of the initial walk, we reduce the degree of every vertex by an even number, so all the vertices of each graph \(G_i\) have even degree. By the induction hypothesis, each \(G_i\) has an Euler circuit. These closed walks together with the original closed walk use every edge of \(G\) exactly once.
Suppose the original closed walk is \(v_0,v_1,\ldots,v_m=v_0\), abbreviated to leave out the edges. Because \(G\) is connected, at least one vertex in each \(G_i\) appears in this sequence, say vertices \(w_{1,1}\in G_1\), \(w_{2,1}\in G_2\),…, \(w_{k,1}\in G_k\), listed in the order they appear in \(v_0,v_1,\ldots,v_m\). The Euler circuits of the graphs \(G_i\) are \[\eqalign{ &w_{1,1},w_{1,2},\ldots,w_{1,m_1}=w_{1,1}\cr &w_{2,1},w_{2,2},\ldots,w_{2,m_2}=w_{2,1}\cr &\vdots\cr &w_{k,1},w_{k,2},\ldots,w_{k,m_k}=w_{k,1}.\cr }\nonumber\] By pasting together the original closed walk with these, we form a closed walk in \(G\) that uses every edge exactly once: \[\eqalign{ v_0,v_1,&\ldots,v_{i_1}=w_{1,1},w_{1,2},\ldots,w_{1,m_1}=v_{i_1},v_{i_1+1},\cr &\ldots, v_{i_2}=w_{2,1},\ldots,w_{2,m_2}=v_{i_2},v_{i_2+1},\cr &\ldots,v_{i_k}=w_{k,1},\ldots,w_{k,m_k}=v_{i_k}, v_{i_k+1},\ldots,v_m=v_0.\cr }\nonumber \]
Now let's turn to the second interpretation of the problem: is it possible to walk over all the bridges exactly once, if the starting and ending points need not be the same? In a graph \(G\), a walk that uses all of the edges but is not an Euler circuit is called an Euler walk. It is not too difficult to do an analysis much like the one for Euler circuits, but it is even easier to use the Euler circuit result itself to characterize Euler walks.
Theorem \(\PageIndex{2}\): Euler Walks
A connected graph \(G\) has an Euler walk if and only if exactly two vertices have odd degree.
- Proof
-
Suppose first that \(G\) has an Euler walk starting at vertex \(v\) and ending at vertex \(w\). Add a new edge to the graph with endpoints \(v\) and \(w\), forming \(G'\). \(G'\) has an Euler circuit, and so by the previous theorem every vertex has even degree. The degrees of \(v\) and \(w\) in \(G\) are therefore odd, while all others are even.
Now suppose that the degrees of \(v\) and \(w\) in \(G\) are odd, while all other vertices have even degree. Add a new edge \(e\) to the graph with endpoints \(v\) and \(w\), forming \(G'\). Every vertex in \(G'\) has even degree, so by the previous theorem there is an Euler circuit which we can write as \[v,e_1,v_2,e_2,\ldots,w,e,v,\nonumber\] so that \[v,e_1,v_2,e_2,\ldots,w\nonumber\] is an Euler walk.


