5.7: Conectividad
- Page ID
- 117088
Hemos visto ejemplos de gráficas conectadas y gráficas que no están conectadas. Si bien “no conectado” es más o menos un callejón sin salida, hay mucho que decir sobre “cuán conectado” está un gráfico conectado. El enfoque más sencillo es observar lo difícil que es desconectar una gráfica eliminando vértices o aristas. Suponemos que todas las gráficas son simples.
Si es posible desconectar una gráfica quitando un solo vértice, llamado punto de corte, decimos que la gráfica tiene conectividad 1. Si esto no es posible, pero es posible desconectar la gráfica eliminando dos vértices, la gráfica tiene conectividad 2.
Definición\(\PageIndex{1}\): Cutset
Si una gráfica\(G\) está conectada, cualquier conjunto de vértices cuya eliminación desconecta la gráfica se denomina conjunto de cortes. \(G\)tiene conectividad\(k\) si hay un juego de corte de tamaño\(k\) pero no un juego de corte más pequeño. Si no hay cutset y\(G\) tiene al menos dos vértices, decimos que\(G\) tiene conectividad\(n-1\); si\(G\) tiene un vértice, su conectividad es indefinida. Si no\(G\) está conectado, decimos que tiene conectividad\(0\). \(G\)está\(k\) -conectado si la conectividad de\(G\) es al menos\(k\). Se denota\(G\) la conectividad de\(\kappa(G)\).
Como debe esperar de la definición, hay gráficas sin un juego de recortes: las gráficas completas\(K_n\). Si\(G\) está conectado pero no a\(K_n\), tiene vértices\(v\) y\(w\) que no son adyacentes, por lo que la eliminación de los\(n-2\) otros vértices deja una gráfica no conectada, y así la conectividad de\(G\) es como mucho\(n-2\). Así, solo las gráficas completas tienen conectividad\(n-1\).
Hacemos lo mismo para los bordes:
Definición\(\PageIndex{2}\): Cut
Si una gráfica\(G\) está conectada, cualquier conjunto de aristas cuya eliminación desconecte la gráfica se denomina corte. \(G\)tiene conectividad de borde\(k\) si hay un corte de tamaño\(k\) pero no menor; la conectividad de borde de un gráfico de un vértice no está definida. \(G\)está\(k\) -borde-conectado si la conectividad de borde de\(G\) es al menos\(k\). Se denota la conectividad perimetral\(\lambda(G)\).
Cualquier gráfico conectado con al menos dos vértices se puede desconectar eliminando bordes: al eliminar todos los bordes incidentes con un solo vértice, el gráfico se desconecta. Así,\(\lambda(G)\le \delta(G)\), donde\(\delta(G)\) está el grado mínimo de cualquier vértice en\(G\). Tenga en cuenta que\(\delta(G)\le n-1\), entonces\(\lambda(G)\le n-1\).
Al quitar un vértice también se eliminan todos los bordes que inciden con él, lo que sugiere que\(\kappa(G)\le\lambda(G)\). Esto resulta ser cierto, aunque no tan fácil como cabría esperar. Escribimos\(G-v\) para significar\(G\) con vértice\(v\) eliminado, y\(G-\{v_1,v_2,\ldots,v_k\}\) para significar\(G\) con todo\(\{v_1,v_2,\ldots,v_k\}\) eliminado, y de manera similar para bordes.
Teorema \(\PageIndex{1}\)
\(\kappa(G)\le\lambda(G)\).
- Prueba
-
Utilizamos inducción en\(\lambda=\lambda(G)\). Si\(\lambda=0\),\(G\) está desconectado, entonces\(\kappa=0\). Si\(\lambda=1\), eliminación de borde\(e\) con puntos finales\(v\) y\(w\) desconexiones\(G\). Si\(v\) y\(w\) son los únicos vértices de\(G\),\(G\) es\(K_2\) y tiene conectividad\(1\). De lo contrario, remoción de uno de\(v\) y\(w\) desconecta\(G\), así\(\kappa=1\).
Como caso especial señalamos que si\(\lambda=n-1\) entonces\(\delta=n-1\), así\(G\) es\(K_n\) y\(\kappa=n-1\).
Ahora supongamos\(n-1>\lambda=k>1\), y la eliminación de bordes\(e_1,e_2,\ldots,e_k\) se desconecta\(G\). Retire el borde\(e_k\) con puntos finales\(v\) y\(w\) para formar\(G_1\) con\(\lambda(G_1)=k-1\). Por la hipótesis de inducción, hay a lo sumo\(k-1\) vértices\(v_1,v_2,\ldots,v_j\) tales que\(G_2=G_1-\{v_1,v_2,\ldots,v_j\}\) se desconectan. Desde\(k< n-1\),\(k-1\le n-3\), y así\(G_2\) tiene al menos\(3\) vértices.
Si ambos\(v\) y\(w\) son vértices de\(G_2\), y si agregar\(e_k\) a\(G_2\) produce una gráfica conectada\(G_3\), entonces la eliminación de uno de\(v\) y\(w\) desconectará la\(G_3\) formación\(G_4\), y\(G_4=G-\{v_1,v_2,\ldots,v_j,v\}\) o\(G_4=G-\{v_1,v_2,\ldots,v_j,w\}\), es decir, la eliminación como máximo \(k\)vértices desconecta\(G\). Si\(v\) y\(w\) son vértices de\(G_2\) pero sumar\(e_k\) no produce una gráfica conectada, entonces eliminar las\(v_1,v_2,\ldots,v_j\) desconexiones\(G\). Por último, si al menos uno de\(v\) y no\(w\) está en\(G_2\), entonces\(G_2=G-\{v_1,v_2,\ldots,v_j\}\) y la conectividad de\(G\) es menor que\(k\). Entonces en todos los casos,\(\kappa\le k\).
Las gráficas que están conectadas en 2 son particularmente importantes, y el siguiente teorema simple es útil.
Teorema \(\PageIndex{2}\)
Si\(G\) tiene al menos tres vértices, los siguientes son equivalentes:
- \(G\)está 2-conectado
- \(G\)está conectado y no tiene ningún punto de corte
- Para todos los vértices distintos\(u\)\(v\),,\(w\) en\(G\) hay un camino desde\(u\) hasta\(v\) que no contiene\(w\).
- Prueba
-
\(\bf 1\Rightarrow3\): Dado que\(G\) es 2-conectado,\(G\) con\(w\) eliminado es una gráfica conectada\(G'\). Así, en\(G'\) hay un camino de\(u\) a\(v\), que en\(G\) es un camino de\(u\) a\(v\) evitar\(w\).
\(\bf 3\Rightarrow2\): Si\(G\) tiene propiedad 3 está claramente conectada. Supongamos que\(w\) es un punto de corte, así que eso\(G'=G-w\) está desconectado. Dejar\(u\) y\(v\) ser vértices en dos componentes diferentes de\(G'\), para que ningún camino los conecte en\(G'\). Entonces todo camino\(u\) que se une\(v\) en\(G\) debe usar\(w\), una contradicción.
\(\bf 2\Rightarrow1\): Dado que\(G\) tiene al menos 3 vértices y no tiene ningún punto de corte, su conectividad es al menos 2, por lo que está 2-conectada por definición.
Hay otras agradables caracterizaciones de 2 gráficas conectadas.
Teorema \(\PageIndex{3}\)
Si\(G\) tiene al menos tres vértices, entonces\(G\) es 2-conectado si y sólo si cada dos vértices\(u\) y\(v\) están contenidos en un ciclo.
- Prueba
-
if: Supongamos que\(w\) el vértice se elimina de\(G\), y considerar cualquier otro vértice\(u\) y\(v\). En\(G\),\(u\) y\(v\) se encuentran en un ciclo; aunque\(w\) también se encuentre en este ciclo, entonces\(u\) y todavía\(v\) están conectados por un camino cuando\(w\) se elimina.
sólo si: Dado\(u\) y\(v\) queremos mostrar hay un ciclo que contiene ambos. Dejar\(U\) ser el conjunto de vértices distintos a los\(u\) que están contenidos en un ciclo con\(u\). Primero, mostramos que no\(U\) está vacío. Dejar\(w\) estar adyacente a\(u\), y quitar el borde\(e\) entre ellos. Ya que\(\lambda(G)\ge \kappa(G)\ge 2\),\(G-e\) está conectado. Así, hay un camino de\(u\) a\(w\); junto con\(e\) este camino forma un ciclo que contiene\(u\) y\(w\), así\(w\in U\).
Por una contradicción, supongamos\(v\notin U\). Dejar entrar\(w\)\(U\) con\(\text{d}(w,v)\ge 1\) lo más pequeño posible, fijar un ciclo\(C\) que contiene\(u\) y\(w\) y una trayectoria\(P\) de longitud\(\text{d}(w,v)\) de\(w\) a\(v\). Por el teorema anterior, hay un camino\(Q\) desde\(u\) hasta\(v\) que no utiliza\(w\). Siguiendo este camino desde\(u\), hay un último vértice\(x\) en el camino que también está en el ciclo que contiene\(u\) y\(w\), y hay un primer vértice\(y\) en el camino, después\(x\), con\(y\) también en el camino de\(w\) a\(v\) (es posible eso\(y=v\), pero no eso\(y=w\)); ver Figura\(\PageIndex{1}\). Ahora a partir de\(u\), procediendo en ciclo\(C\) a\(x\) sin usar\(w\), luego de\(x\) a\(y\) adelante\(Q\), luego a\(w\) encendido\(P\), y finalmente de nuevo a\(u\) encendido\(C\), vemos eso\(y\in U\). Pero\(y\) está más cerca\(v\) de lo que es\(w\), una contradicción. De ahí\(v\in U\).
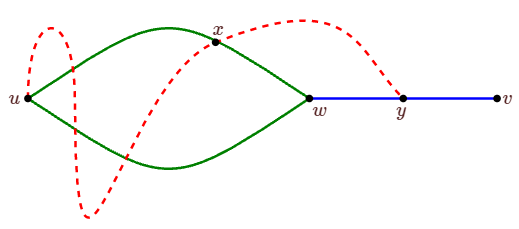
El siguiente corolario es una fácil reafirmación de este teorema.
Corolario \(\PageIndex{1}\)
Si\(G\) tiene al menos tres vértices, entonces\(G\) es 2-conectado si y sólo si entre cada dos vértices\(u\) y\(v\) hay dos caminos internamente disjuntos entre\(v\) y\(w\), es decir, caminos que comparten sólo los vértices\(v\) y\(w\).
Esta versión del teorema sugiere una generalización:
Teorema \(\PageIndex{4}\): Menger's Theorem
Si\(G\) tiene al menos\(k+1\) vértices, entonces\(G\) está\(k\) -conectado si y solo si entre cada dos vértices\(u\) y\(v\) hay caminos internamente disjuntos por\(k\) pares.
- Prueba
-
Supongamos primero que entre cada dos vértices\(v\) y\(w\) adentro\(G\) hay caminos\(k\) internamente disjuntos. Si no\(G\) está\(k\) -conectado, la conectividad de\(G\) es como mucho\(k-1\), y debido a que\(G\) tiene al menos\(k+1\) vértices, hay un cutset\(S\) de\(G\) con tamaño como máximo\(k-1\). Let\(v\) y\(w\) ser vértices en dos componentes diferentes de\(G-S\); en\(G\) estos vértices están unidos por caminos\(k\) internamente disjuntos. Como no hay camino de\(v\) a\(w\) adentro\(G-S\), cada uno de estos\(k\) caminos contiene un vértice de\(S\), pero esto es imposible ya que\(S\) tiene un tamaño menor que\(k\), y los caminos no comparten vértices distintos de\(v\) y\(w\). Esta contradicción muestra que\(G\) está\(k\) -conectado.
Ahora supongamos que\(G\) está\(k\) -conectado.
Si\(v\) y no\(w\) son adyacentes,\(\kappa_G(v,w)\ge k\) y por el teorema anterior hay caminos\(p_G(v,w)=\kappa_G(v,w)\) internamente disjuntos entre\(v\) y\(w\).
Si\(v\) y\(w\) están conectados por borde\(e\), considere\(G-e\). Si hay un cutset\(G-e\) de tamaño menor que\(k-1\), llámelo\(S\), entonces cualquiera\(S\cup\{v\}\) o\(S\cup\{w\}\) es un cutset\(G\) de tamaño menor que\(k\), una contradicción. (Dado que\(G\) tiene al menos\(k+1\) vértices,\(G-S\) tiene al menos tres vértices.) Así,\(\kappa_{G-e}(v,w)\ge k-1\) y por el teorema anterior hay al menos caminos\(k-1\) internamente disjuntos entre\(v\) y\(w\) en\(G-e\). Junto con el camino\(v\),\(w\) usando el borde\(e\), estos forman caminos\(k\) internamente disjuntos entre\(v\) y\(w\) dentro\(G\).
Primero probamos la versión original de Menger de esta, una versión “local”.
Definition \(\PageIndex{3}\): Separating Set
If \(v\) and \(w\) are non-adjacent vertices in \(G\), \(\kappa_G(v,w)\) is the smallest number of vertices whose removal separates \(v\) from \(w\), that is, disconnects \(G\) leaving \(v\) and \(w\) in different components. A cutset that separates \(v\) and \(w\) is called a separating set for \(v\) and \(w\). \(p_G(v,w)\) is the maximum number of internally disjoint paths between \(v\) and \(w\).
If \(v\) and \(w\) are non-adjacent vertices in \(G\), \(\kappa_G(v,w)=p_G(v,w)\).
- Proof
-
If there are \(k\) internally disjoint paths between \(v\) and \(w\), then any set of vertices whose removal separates \(v\) from \(w\) must contain at least one vertex from each of the \(k\) paths, so \(\kappa_G(v,w)\ge p_G(v,w)\).
To finish the proof, we show that there are \(\kappa_G(v,w)\) internally disjoint paths between \(v\) and \(w\). The proof is by induction on the number of vertices in \(G\). If \(G\) has two vertices, \(G\) is not connected, and \(\kappa_G(v,w)=p_G(v,w)=0\). Now suppose \(G\) has \(n>2\) vertices and \(\kappa_G(v,w)=k\).
Note that removal of either \(N(v)\) or \(N(w)\) separates \(v\) from \(w\), so no separating set \(S\) of size \(k\) can properly contain \(N(v)\) or \(N(w)\). Now we address two cases:
Case 1: Suppose there is a set \(S\) of size \(k\) that separates \(v\) from \(w\), and \(S\) contains a vertex not in \(N(v)\) or \(N(w)\). \(G-S\) is disconnected, and one component \(G_1\) contains \(v\). Since \(S\) does not contain \(N(v)\), \(G_1\) has at least two vertices; let \(X=V(G_1)\) and \(Y=V(G)-S-X\). Since \(S\) does not contain \(N(w)\), \(Y\) contains at least two vertices. Now we form two new graphs: Form \(H_X\) by starting with \(G-Y\) and adding a vertex \(y\) adjacent to every vertex of \(S\). Form \(H_Y\) by starting with \(G-X\) and adding a vertex \(x\) adjacent to every vertex of \(S\); see Figure \(\PageIndex{2}\). Since \(X\) and \(Y\) each contain at least two vertices, \(H_X\) and \(H_Y\) are smaller than \(G\), and so the induction hypothesis applies to them.
Clearly \(S\) separates \(v\) from \(y\) in \(H_X\) and \(w\) from \(x\) in \(H_Y\). Moreover, any set that separates \(v\) from \(y\) in \(H_X\) separates \(v\) from \(w\) in \(G\), so \(\kappa_{H_X}(v,y)=\kappa_G(v,w)=k\). Similarly, \(\kappa_{H_Y}(x,w)=\kappa_G(v,w)=k\). Hence, by the induction hypothesis, there are \(k\) internally disjoint paths from \(v\) to \(y\) in \(H_X\) and \(k\) internally disjoint paths from \(x\) to \(w\) in \(H_Y\). Each of these paths uses one vertex of \(S\); by eliminating \(x\) and \(y\) and joining the paths at the vertices of \(S\), we produce \(k\) internally disjoint paths from \(v\) to \(w\).
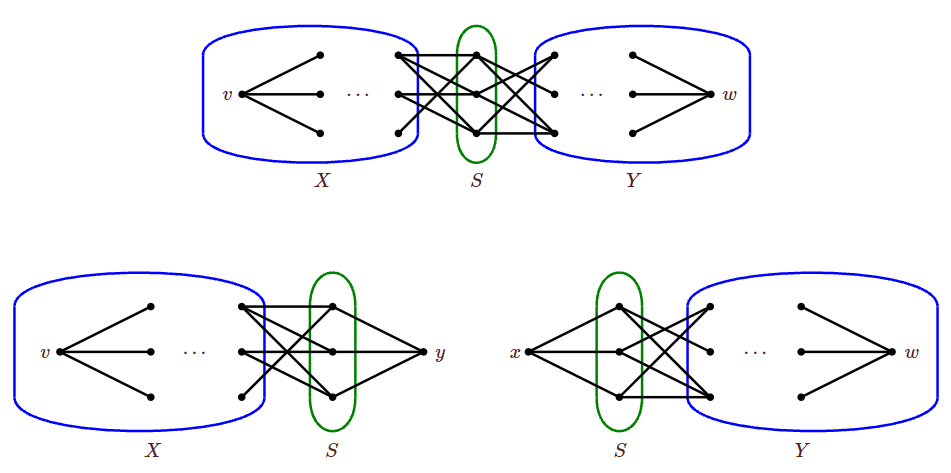
Figure \(\PageIndex{2}\): Case 1: Top figure is \(G\), lower left is \(H_X\), lower right is \(H_Y\). Case 2: Now we suppose that any set \(S\) separating \(v\) and \(w\) is a subset of \(N(v)\cup N(w)\); pick such an \(S\). If there is a vertex \(u\) not in \(\{v,w\}\cup N(v)\cup N(w)\), consider \(G-u\). This \(u\) is not in any set of size \(k\) that separates \(v\) from \(w\), for if it were we would be in Case 1. Since \(S\) separates \(v\) from \(w\) in \(G-u\), \(\kappa_{G-u}(v,w)\le k\). But if some smaller set \(S'\) separates \(v\) from \(w\) in \(G-u\), then \(S'\cup\{u\}\) separates \(v\) from \(w\) in \(G\), a contradiction, so \(\kappa_{G-u}(v,w)=k\). By the induction hypothesis, there are \(k\) internally disjoint paths from \(v\) to \(w\) in \(G-u\) and hence in \(G\).
We are left with \(V(G)=\{v,w\}\cup N(v)\cup N(w)\). Suppose there is a vertex \(u\) in \(N(v)\cap N(w)\). Then \(u\) is in every set that separates \(v\) from \(w\), so \(\kappa_{G-u}=k-1\). By the induction hypothesis, there are \(k-1\) internally disjoint paths from \(v\) to \(w\) in \(G-u\) and together with the path \(v,u,w\), they comprise \(k\) internally disjoint paths from \(v\) to \(w\) in \(G\). Finally, suppose that \(N(v)\cap N(w)=\emptyset\). Form a bipartite graph \(B\) with vertices \(N(v)\cup N(w)\) and any edges of \(G\) that have one endpoint in \(N(v)\) and the other in \(N(w)\). Every set separating \(v\) from \(w\) in \(G\) must include one endpoint of every edge in \(B\), that is, must be a vertex cover in \(B\), and conversely, every vertex cover in \(B\) separates \(v\) from \(w\) in \(G\). Thus, the minimum size of a vertex cover in \(B\) is \(k\), and so there is a matching in \(B\) of size \(k\), by Theorem 4.6.4. The edges of this matching, together with the edges incident at \(v\) and \(w\), form \(k\) internally disjoint paths from \(v\) to \(w\) in \(G\).
\[\bullet\quad\bullet\quad\bullet\nonumber\]
We return briefly to 2-connectivity. The next theorem can sometimes be used to provide the induction step in an induction proof.
Theorem \(\PageIndex{6}\): The Handle Theorem
Suppose \(G\) is 2-connected and \(K\) is a 2-connected proper subgraph of \(G\). Then there are subgraphs \(L\) and \(H\) (the handle) of \(G\) such that \(L\) is 2-connected, \(L\) contains \(K\), \(H\) is a simple path, \(L\) and \(H\) share exactly the endpoints of \(H\), and \(G\) is the union of \(L\) and \(H\).
- Proof
-
Given \(G\) and \(K\), let \(L\) be a maximal proper subgraph of \(G\) containing \(K\). If \(V(L)=V(G)\), let \(e\) be an edge not in \(L\). Since \(L\) plus the edge \(e\) is 2-connected, it must be \(G\), by the maximality of \(L\). Hence \(H\) is the path consisting of \(e\) and its endpoints.
Suppose that \(v\) is in \(V(G)\) but not \(V(L)\). Let \(u\) be a vertex of \(L\). Since \(G\) is 2-connected, there is a cycle containing \(v\) and \(u\). Following the cycle from \(v\) to \(u\), Let \(w\) be the first vertex in \(L\). Continuing on the cycle from \(u\) to \(v\), let \(x\) be the last vertex in \(L\). Let \(P\) be the path continuing around the cycle: \((x,v_1,v_2,\ldots,v_k,v=v_{k+1},v_{k+2},\ldots,v_m,w)\). If \(x\not=w\), let \(H=P\). Since \(L\) together with \(H\) is 2-connected, it is \(G\), as desired.
If \(x=w\) then \(x=w=u\). Let \(y\) be a vertex of \(L\) other than \(u\). Since \(G\) is 2-connected, there is a path \(P_1\) from \(v\) to \(y\) that does not include \(u\). Let \(v_j\) be the last vertex on \(P_1\) that is in \(\{v_1,\ldots,v,\ldots,v_m\}\); without loss of generality, suppose \(j\ge k+1\). Then let \(H\) be the path \((u,v_1,\ldots,v=v_{k+1},\ldots, v_j,\ldots,y)\), where from \(v_j\) to \(y\) we follow path \(P_1\). Now \(L\cup H\) is a 2-connected subgraph of \(G\), but it is not \(G\), as it does not contain the edge \(\{u,v_m\}\), contradicting the maximality of \(L\). Thus \(x\not=w\).
A graph that is not connected consists of connected components. In a theorem reminiscent of this, we see that connected graphs that are not 2-connected are constructed from 2-connected subgraphs and bridges.
Definition \(\PageIndex{4}\): Block
A block in a graph \(G\) is a maximal induced subgraph on at least two vertices without a cutpoint.
As usual, maximal here means that the induced subgraph \(B\) cannot be made larger by adding vertices edges. A block is either a 2-connected induced subgraph or a single edge together with its endpoints. Blocks are useful in large part because of this theorem:
The blocks of \(G\) partition the edges.
- Proof
-
We need to show that every edge is in exactly one block. If an edge is in no 2-connected induced subgraph of \(G\), then, together with its endpoints, it is itself a block. Thus, every edge is in some block.
Now suppose that \(B_1\) and \(B_2\) are distinct blocks. This implies that neither is a subgraph of the other, by the maximality condition. Hence, the induced subgraph \(G[V(B_1)\cup V(B_2)]\) is larger than either of \(B_1\) and \(B_2\). Suppose \(B_1\) and \(B_2\) share an edge, so that they share the endpoints of this edge, say \(u\) and \(v\). Supppose \(w\) is a vertex in \(V(B_1)\cup V(B_2)\). Since \(B_1-w\) and \(B_2-w\) are connected, so is \(G[(V(B_1)\cup V(B_2))\backslash\{w\}]\), because either \(u\) or \(v\) is in \((V(B_1)\cup V(B_2))\backslash\{w\}\). Thus \(G[V(B_1)\cup V(B_2)]\) has no cutpoint and so it is 2-connected and strictly contains \(B_1\) and \(B_2\), contradicting the maximality property of blocks. Thus, every edge is in at most one block.
If \(G\) has a single block, it is either \(K_2\) or is 2-connected, and any 2-connected graph has a single block.
If \(G\) is connected but not 2-connected, then every vertex that is in two blocks is a cutpoint of \(G\).
- Proof
-
Suppose \(w\) is in \(B_1\) and \(B_2\), but \(G-w\) is connected. Then there is a path \(v_1,v_2,\ldots,v_k\) in \(G-w\), with \(v_1\in B_1\) and \(v_k\in B_2\). But then \(G[V(B_1)\cup V(B_2)\cup \{v_1,v_2,\ldots,v_k\}]\) is 2-connected and contains both \(B_1\) and \(B_2\), a contradiction.


