2.1: Técnicas Básicas de Conteo - La Regla de los Productos

Última actualización
Guardar como PDF

Page ID: 117292

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

¿Combinatoria?

Uno de los primeros conceptos que nos enseñaron nuestros padres fue el “arte de contar”. Nos enseñaron a levantar tres dedos para indicar que teníamos tres años. La pregunta de “cuántos” es una pregunta natural y frecuente. La combinatoria es el “arte de contar”. Es el estudio de técnicas que nos ayudarán a contar rápidamente el número de objetos en un conjunto. Con este sencillo concepto se pueden obtener resultados altamente sofisticados. Los siguientes ejemplos ilustrarán que muchas preguntas relacionadas con el conteo involucran el mismo proceso.

Ejemplo $\PageIndex{1}$: How Many Lunches Can You Have?

Un snack bar sirve cinco sándwiches diferentes y tres bebidas diferentes. ¿Cuántos almuerzos diferentes puede pedir una persona? Una forma de determinar el número de posibles almuerzos es enumerando o enumerando todas las posibilidades. Una forma sistemática de hacerlo es por medio de un árbol, como en la siguiente figura.

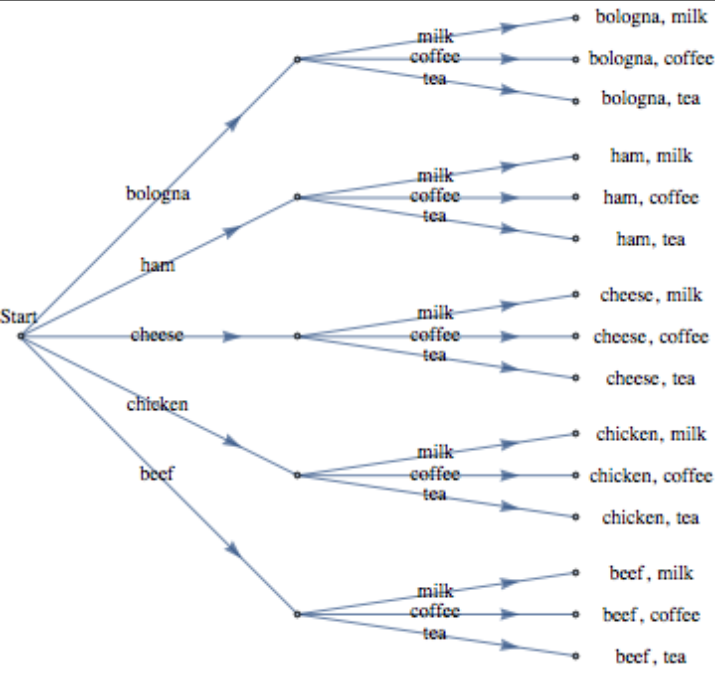
Cada camino que comienza en la posición etiquetada START y va hacia la derecha puede interpretarse como una elección de uno de los cinco sándwiches seguido de una elección de una de las tres bebidas. Tenga en cuenta que se requiere un trabajo considerable para llegar al número quince de esta manera; pero también obtenemos algo más que un número. El resultado es una lista completa de todos los almuerzos posibles. Si necesitamos responder a una pregunta que comience con “Cuantos..”, la enumeración se haría sólo como último recurso. En un capítulo posterior examinaremos más técnicas de enumeración.

Un método alternativo de solución para este ejemplo es hacer la simple observación de que hay cinco opciones diferentes para sándwiches y tres opciones diferentes para bebidas, por lo que hay$5 \cdot 3 = 15$ diferentes almuerzos que se pueden pedir.

Ejemplo$\PageIndex{2}$: Counting Elements in a Cartesian Product

Vamos$A = \{a, b, c, d, e\}$ y$B = \{1,2,3\}\text{.}$ A partir del Capítulo 1 sabemos cómo enumerar los elementos en$A \times B = \{(a, 1), (a, 2), (a, 3), ..., (e, 3)\}\text{.}$ Dado que la primera entrada de cada par puede ser cualquiera de los cinco elementos$a, b, c, d\text{,}$$e\text{,}$ y y como el segundo puede ser cualquiera de los tres números 1, 2 y 3, es bastante claro que hay$5 \cdot 3 = 15$ diferentes elementos en$A \times B\text{.}$

Ejemplo$\PageIndex{3}$: A True-False Questionnaire

Una persona debe completar un cuestionario verdadero-falso que consta de diez preguntas. ¿Cuántas formas diferentes hay de responder el cuestionario? Dado que cada pregunta puede ser respondida de dos maneras (verdadera o falsa), y hay diez preguntas, hay

\ begin {ecuación*} 2\ cdot 2\ cdot 2\ cdot 2\ cdot 2\ cdot 2\ cdot 2\ cdot 2\ cdot 2\ cdot 2\ cdot 2 = 2^ {10} = 1024\ final {ecuación*}

diferentes formas de responder al cuestionario. Se anima al lector a visualizar el diagrama de árbol de este ejemplo, ¡pero no a dibujarlo!

Formalizamos los procedimientos desarrollados en los ejemplos anteriores con la siguiente regla y su extensión.

Regla de productos

Si se deben realizar dos operaciones, y si la primera operación siempre se puede realizar de$p_1$ diferentes maneras y la segunda operación siempre se puede realizar de$p_2$ diferentes maneras, entonces hay$p_1 p_2$ diferentes formas en que se pueden realizar las dos operaciones.

Nota$\PageIndex{1}$

Es importante que$p_2$ no dependa de la opción que se elija en la primera operación. Otra forma de decir esto es que$p_2$ es independiente de la primera operación. Si$p_2$ depende de la primera operación, entonces no se aplica la regla de productos.

Ejemplo$\PageIndex{4}$: Reduced Lunch Possibilities

Supongamos en Ejemplo$\PageIndex{1}$, el café no se sirve con unos sándwiches de carne de res o pollo. Entonces por inspección de Figura$\PageIndex{1}$ vemos que solo hay trece opciones diferentes para el almuerzo. La regla de los productos no se aplica, ya que la elección de la bebida depende de la elección de un sándwich.

Regla Extendida De Productos. La regla de productos se puede extender para incluir secuencias de más de dos operaciones. Si se deben realizar$n$ operaciones, y el número de opciones para cada operación es$p_1\text{,}$$p_2, \dots, p_n$ respectivamente, con cada una$p_i$ independiente de las elecciones anteriores, entonces las$n$ operaciones se pueden realizar de$p_1 \cdot p_2 \cdot \cdots \cdot p_n$ diferentes maneras.

Ejemplo$\PageIndex{5}$: A Multiple Choice Questionnaire

Un cuestionario contiene cuatro preguntas que tienen dos respuestas posibles y tres preguntas con cinco respuestas posibles. Dado que la respuesta a cada pregunta es independiente de las respuestas a las otras preguntas, se aplica la regla extendida de productos y existen$2 \cdot 2 \cdot 2 \cdot 2 \cdot 5 \cdot 5 \cdot 5 = 2^4 \cdot 5^3 = 2000 $ diferentes formas de responder al cuestionario.

En el Capítulo 1 introducimos el conjunto de potencias de un conjunto$A\text{,}$$\mathcal{P}(A)\text{,}$ que es el conjunto de todos los subconjuntos de$A\text{.}$ Can we predict how many elements are in$\mathcal{P}(A)$ for a given finite set$A\text{?}$ La respuesta es sí, y de hecho si$\lvert A \rvert = n\text{,}$ entonces$\lvert \mathcal{P}(A) \rvert = 2^{n}\text{.}$ La facilidad con la que podemos demostrar este hecho demuestra el poder y utilidad de la regla de los productos. No subestimes la utilidad de las ideas simples.

Teorema$\PageIndex{1}$: Power Set Cardinality Theorem

Si$A$ es un conjunto finito, entonces$\lvert \mathcal{P}(A) \rvert = 2^{\lvert A \rvert }\text{.}$

Prueba

Consideremos cómo podríamos determinar cualquier$B \in \mathcal{P}(A)\text{,}$ lugar$\lvert A \rvert =n\text{.}$ Para cada elemento$x \in A$ hay dos opciones, ya sea$x \in B$ o$x \notin B\text{.}$ Ya que hay$n$ elementos de$A$ tenemos, por la regla de los productos,

\ begin {ecuación*}\ underset {n\ textrm {factores}} {\ subrayado {2\ cdot 2\ cdot\ cdot\ cdots\ cdot 2}} = 2^n\ end {ecuación*}

diferentes subconjuntos de$A\text{.}$ Por lo tanto,$\mathcal{P}(A)= 2^{n}\text{.}$

Ejercicios

Ejercicio$\PageIndex{1}$

En las carreras de caballos, apostar el “doble diario” es seleccionar a los ganadores de las dos primeras carreras del día. Usted gana sólo si ambas selecciones son correctas. En cuanto al número de caballos que se ingresan en las dos primeras carreras, ¿cuántas apuestas dobles diarias diferentes podrían hacerse?

Responder: Si hay$m$ caballos en la carrera 1 y$n$ caballos en la carrera 2 entonces hay$m \cdot n$ posibles dobles diarios.

Ejercicio$\PageIndex{2}$

El profesor Shortcut registra sus calificaciones usando solo la primera y última iniciales de sus alumnos. ¿Cuál es el tamaño de clase más pequeño que definitivamente obligará al Prof. S. a usar un sistema diferente?

Ejercicio$\PageIndex{3}$

Cierta playera viene en cuatro tallas y seis colores. Uno también tiene la opción de un dragón, un cocodrilo, o ningún emblema en el bolsillo. ¿Cuántas camisas diferentes podrías pedir?

Responder: $72=4\cdot 6\cdot 3$

Ejercicio$\PageIndex{4}$

A un constructor de casas modulares le gustaría impresionar a sus clientes potenciales con la variedad de estilos de sus casas. Para cada casa hay planos para tres salas de estar diferentes, cuatro configuraciones de recámara diferentes y dos estilos de cochera diferentes. Además, el exterior se puede terminar en tejas de cedro o ladrillo. ¿Cuántas casas diferentes se pueden diseñar a partir de estos planos?

Ejercicio$\PageIndex{5}$

La sociedad honoraria de matemáticas Pi Mu Epsilon de la Universidad Sobresaliente desea que se le tome una foto de sus seis oficiales. Habrá dos filas de tres personas. ¿De cuántas maneras diferentes se pueden arreglar los seis oficiales?

Responder: $720=6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1$

Ejercicio$\PageIndex{6}$

Un concesionario de automóviles tiene varias opciones disponibles para cada uno de los tres paquetes diferentes de un modelo de automóvil en particular: una opción de dos estilos de asientos en tres colores diferentes, una opción de cuatro radios diferentes y cinco exteriores diferentes. ¿Cuántas opciones de automóvil tiene un cliente?

Ejercicio$\PageIndex{7}$

Un fabricante de ropa ha sacado una colección mix-and-match compuesta por dos blusas, dos pares de pantalones, una falda y un blazer. ¿Cuántos atuendos puedes hacer? ¿Consideraste que el blazer es opcional? ¿Cuántos atuendos puedes hacer si el fabricante agrega un jersey a la colección?

Responder: Si siempre incluimos el blazer en el atuendo tendríamos 6 outfits. Si consideramos el blazer opcional entonces habría 12 atuendos. Cuando agregamos un jersey tenemos el mismo tipo de elección. Considerando el suéter opcional produce 24 atuendos.

Ejercicio$\PageIndex{8}$

Como estudiante de primer año, supongamos que tuvo que tomar dos de cuatro cursos de ciencias de laboratorio, uno de dos cursos de literatura, dos de tres cursos de matemáticas y uno de siete cursos de educación física. Sin tener en cuenta los posibles conflictos de tiempo, ¿cuántos horarios diferentes tienes para elegir?

Ejercicio$\PageIndex{9}$

Supongamos que cada carácter único almacenado en una computadora usa ocho bits. Entonces cada carácter es representado por una secuencia diferente de ocho 0 y 1 llamada patrón de bits. ¿Cuántos patrones de bits diferentes hay? (Es decir, ¿cuántos personajes diferentes podrían representarse?)
¿Cuántos patrones de bits son los palíndromos (lo mismo hacia atrás que hacia adelante)?
¿Cuántos patrones de bits diferentes tienen un número par de 1's?

Responder

$\displaystyle 2^8=256$
$2^4=16\text{.}$Aquí nos preocupan sólo los primeros cuatro bits, ya que los últimos cuatro deben ser los mismos.
$2^7=128\text{,}$no tienes otra opción en el último bit.

Ejercicio$\PageIndex{10}$

Las placas de automóviles en Massachusetts suelen consistir en tres dígitos seguidos de tres letras. El primer dígito nunca es cero. ¿Cuántas placas diferentes de este tipo se podrían hacer?

Ejercicio$\PageIndex{11}$

Dejar$A = \{1, 2, 3, 4\}\text{.}$ Determinar el número de diferentes subconjuntos de$A\text{.}$
Deje$A = \{1, 2, 3, 4, 5\}\text{.}$ Determinar el número de subconjuntos adecuados de$A$.

Responder

$\displaystyle 16$
$\displaystyle 31$

Ejercicio$\PageIndex{12}$

¿Cuántos enteros de 100 a 999 se pueden escribir en base diez sin usar el dígito 7?

Ejercicio$\PageIndex{13}$

Considera a tres personas, A, B y C, que van a estar sentadas en fila de tres sillas. Supongamos que A y B son gemelos idénticos. ¿Cuántas disposiciones de asientos de estas personas puede haber?

¿Si eres un desconocido total?
¿Si eres la madre de A y B?

Este problema está diseñado para mostrarte que diferentes personas pueden tener diferentes respuestas correctas al mismo problema.

Responder

$\displaystyle 3$
$\displaystyle 6$

Ejercicio$\PageIndex{14}$

¿De cuántas maneras puede un estudiante hacer un examen verdadero-falso de diez preguntas si puede optar por no responder a ninguna cantidad de preguntas?

Ejercicio$\PageIndex{15}$

Supongamos que tiene la opción de pescado, cordero o carne de res para un plato principal, una opción de guisantes o zanahorias para una verdura y una opción de pastel, pastel o helado para el postre. Si debes pedir un artículo de cada categoría, ¿cuántas cenas diferentes son posibles?

Responder: $18$

Ejercicio$\PageIndex{16}$

Supongamos que tiene una opción de vainilla, chocolate o fresa para helado, una opción de maní o nueces para nueces picadas y una opción de dulce de leche caliente o malvavisco para cubrir. Si debes pedir un artículo de cada categoría, ¿cuántos sundaes diferentes son posibles?

Ejercicio$\PageIndex{17}$

Un cuestionario contiene seis preguntas cada una con respuestas sí-no. Para cada respuesta sí, hay una pregunta de seguimiento con cuatro posibles respuestas.

Dibuja un diagrama de árbol que ilustre cuántas formas se puede responder una sola pregunta en el cuestionario.
¿De cuántas formas se puede responder el cuestionario?

Responder

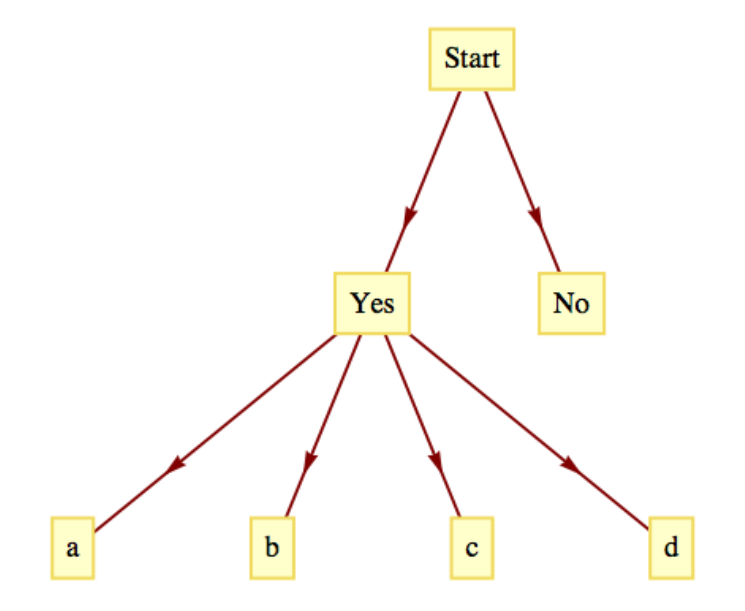
$clipboard_e6f2e1b10417901c8c54dbf4d3b926cf4.png$

Figura$\PageIndex{2}$: Solución al ejercicio$\PageIndex{17}$ (a).

Ver Figura$\PageIndex{2}$
$\displaystyle 5^6$

Ejercicio$\PageIndex{18}$

Diez personas están invitadas a una cena. ¿De cuántas maneras hay de sentarlos en una mesa redonda? Si las diez personas constan de cinco hombres y cinco mujeres, ¿cuántas formas hay de sentarlas si cada hombre debe estar rodeado de dos mujeres alrededor de la mesa?

Ejercicio$\PageIndex{19}$

¿De cuántas maneras se puede separar un conjunto con$n$ elementos en dos subconjuntos no vacíos si el orden de los subconjuntos es inmaterial? ¿Y si el orden de los subconjuntos es importante?

Responder: $2^{n-1}-1$y$2^n-2$

Ejercicio$\PageIndex{20}$

Un jardinero tiene tres arbustos con flores y cuatro arbustos no florecientes, donde todos los arbustos son distinguibles entre sí. Debe plantar estos arbustos en fila utilizando un patrón alterno, es decir, un arbusto debe ser de un tipo diferente al de cada lado. ¿De cuántas maneras puede plantar estos arbustos? Si tiene que plantar estos arbustos en un círculo usando el mismo patrón, ¿de cuántas maneras puede plantar este círculo? Tenga en cuenta que un arbusto no floreciente quedará fuera al final.