2.2: Permutaciones

Ordenar cosas

Una serie de aplicaciones de la regla de los productos son de un tipo específico, y por su frecuente aparición se les da su propia designación, permutaciones. Considera los siguientes ejemplos.

Ejemplo\(\PageIndex{1}\): Ordering the Elements of a Set

De cuántas maneras diferentes podemos ordenar los tres elementos diferentes del conjunto\(A = \{a, b, c\}\text{?}\) Dado que tenemos tres opciones para la posición uno, dos opciones para la posición dos, y una opción para la tercera posición, tenemos, por regla de productos,\(3 \cdot 2 \cdot 1 = 6\) diferentes formas de ordenar las tres letras. Ilustramos a través de un diagrama de árbol.

Figura\(\PageIndex{1}\): Un árbol para enumerar permutaciones de un conjunto de tres elementos.

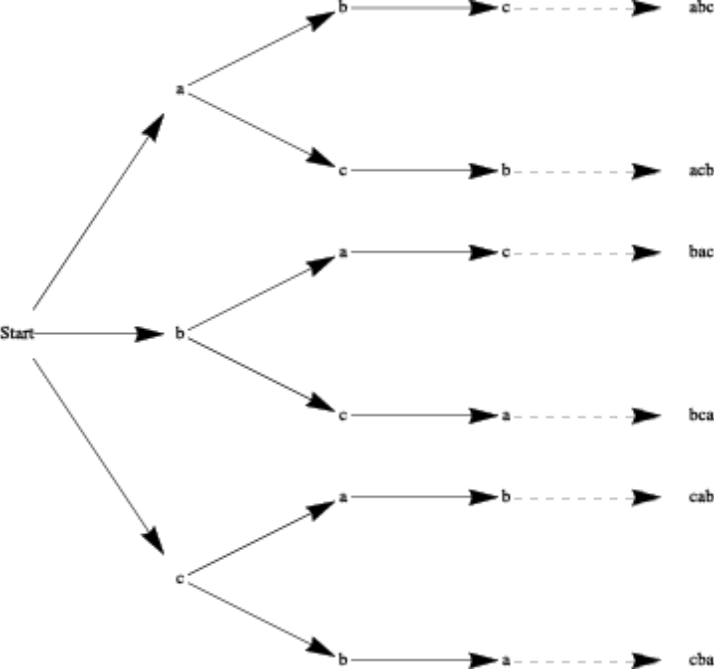
Cada uno de los seis ordenamientos se llama permutación del conjunto\(A\text{.}\)

Ejemplo\(\PageIndex{2}\): Ordering a Schedule

Un estudiante está tomando cinco cursos en el semestre de otoño. ¿De cuántas formas diferentes se pueden enumerar los cinco cursos? Existen\(5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120\) diferentes permutaciones del conjunto de cursos.

En cada uno de los ejemplos anteriores de la regla de productos observamos que:

1. Se nos pide ordenar u organizar elementos de un solo conjunto.
2. Cada elemento se enumera exactamente una vez en cada lista (permutación). Entonces, si hay\(n\) opciones para la posición uno en una lista, hay\(n - 1\) opciones para la posición dos,\(n - 2\) opciones para la posición tres, etc.

Ejemplo\(\PageIndex{3}\): Some Orderings of a Baseball Team

El orden alfabético de los jugadores de un equipo de beisbol es una permutación del conjunto de jugadores. Otros ordenamientos de los nombres de los jugadores se pueden hacer por promedio de bateo, edad o altura. La información que determina el orden se llama clave. Esperaríamos que cada clave diera una permutación diferente de los nombres. Si hay veinticinco jugadores en el equipo, hay\(25 \cdot 24 \cdot 23 \cdot \cdots \cdot 3 \cdot 2 \cdot 1\) diferentes permutaciones de los jugadores.

Este número de permutaciones es enorme. De hecho es 15511210043330985984000000, pero escribirlo así no es tan instructivo, si bien dejarlo como producto como originalmente teníamos hace que sea más fácil ver de dónde viene el número. Solo necesitamos encontrar una forma más compacta de escribir estos productos.

Ahora desarrollamos notación que será útil para problemas de permutación.

Definición \(\PageIndex{1}\): Factorial

Si\(n\) es un entero positivo entonces\(n\) factorial es el producto de los primeros enteros\(n\) positivos y se denota\(n!\text{.}\) Adicionalmente, definimos cero factorial,\(0!\text{,}\) para ser 1.

Las primeras factoriales son

\ begin {ecuation*}\ begin {array} {ccccccccc} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7\\ n! & 1 & 1 & 2 & 6 & 24 & 120 & 720 & 5040\\ end {array}\ text {.} \ end {ecuación*}

Tenga en cuenta que\(4!\) es 4 veces\(3!\text{,}\) o 24, y\(5!\) es 5 veces\(4!\text{,}\) o 120. Además, tenga en cuenta que a medida que\(n\) crece en tamaño,\(n!\) crece extremadamente rápido. Por ejemplo,\(11! = 39916800\text{.}\) si la respuesta a un problema pasa a ser\(25!\text{,}\) como en el ejemplo anterior, nunca se esperaría que escribieras ese número por completo. Sin embargo, un problema con una respuesta de\(\frac{25!}{23!}\) puede reducirse a\(25 \cdot 24\text{,}\) o 600.

Si\(\lvert A \rvert = n \text{,}\) hay\(n!\) formas de permutar todos los\(n\) elementos de\(A\). A continuación consideramos la situación más general en la que nos gustaría permutar\(k\) elementos de un conjunto de\(n\) objetos, donde\(k \leq n\text{.}\)

Ejemplo\(\PageIndex{4}\): Choosing Club Officers

Un club de veinticinco integrantes llevará a cabo una elección para presidente, secretario y tesorero en ese orden. Supongamos que una persona sólo puede ocupar una posición. ¿De cuántas maneras hay de elegir a estos tres oficiales? Por regla de productos hay\(25 \cdot 24 \cdot 23\) formas de hacer una selección.

Definición\(\PageIndex{2}\): Permutation

Una disposición ordenada de\(k\) elementos seleccionados de un conjunto de\(n\) elementos,\(0 \leq k \leq n\text{,}\) donde no hay dos elementos del arreglo iguales, se denomina permutación de\(n\) objetos tomados\(k\) a la vez. El número total de tales permutaciones se denota por\(P(n, k)\text{.}\)

Teorema \(\PageIndex{1}\): Permutation Counting Formula

El número de posibles permutaciones de\(k\) elementos tomados de un conjunto de\(n\) elementos es

\ begin {ecuación*} P (n, k) =n\ cdot (n-1)\ cdot (n-2)\ cdot\ cdot\ cdots\ cdot (n-k+1) =\ prod_ {j=0} ^ {k-1} (n-j) =\ frac {n!} {(n-k)!} \ texto {.} \ end {ecuación*}

Prueba

Caso I: Si\(k = n\) tenemos\(P(n,n)=n!=\frac{n!}{(n-n)!}\text{.}\)

Caso II: Si\(0 \leq k < n\text{,}\) entonces tenemos\(k\) posiciones para llenar usando\(n\) elementos y

1. La posición 1 puede ser llenada por cualquiera de\(n-0=n\) los elementos
2. La posición 2 puede ser llenada por cualquiera de\(n-1\) los elementos
3. \(\displaystyle \cdots \)
4. La posición k puede ser llenada por cualquiera de\(n-(k-1)=n-k+1\) los elementos

De ahí que, por regla de los productos,

\[P(n,k)=n\cdot (n-1)\cdot (n-2)\cdots (n-k+1)=\frac{n!}{(n-k)!}.\nonumber\]

Es importante señalar que la derivación de la fórmula de permutación dada anteriormente se realizó únicamente a través de la regla de productos. Esto sirve para reiterar nuestras observaciones introductorias en esta sección de que los problemas de permutación son realmente problemas de reglas de productos. Cerramos esta sección con varios ejemplos.

Ejemplo\(\PageIndex{5}\): Another Example of Choosing Officers

Un club tiene ocho miembros elegibles para servir como presidente, vicepresidente y tesorero. ¿Cuántas formas hay de elegir a estos oficiales?

Solución 1: Usar la regla de productos. Hay ocho opciones posibles para la presidencia, siete para la vicepresidencia y seis para el cargo de tesorero. Por regla de productos hay\(8 \cdot 7\cdot 6 = 336\) formas de elegir a estos oficiales.

Solución 2: Usando la fórmula de permutación. Queremos que el número total de permutaciones de ocho objetos tomados de tres a la vez:

\ begin {ecuación*} P (8,3) =\ frac {8!} {(8-3)!} =8\ cdot 7\ cdot 6 = 336\ final {ecuación*}

Ejemplo\(\PageIndex{6}\): Course Ordering, Revisited

Para contar el número de formas de ordenar cinco cursos, podemos usar la fórmula de permutación. Queremos el número de permutaciones de cinco cursos tomados cinco a la vez:

\ begin {ecuación*} P (5,5) =\ frac {5!} {(5-5)!} = 5! = 120\ texto {.} \ end {ecuación*}

Ejemplo\(\PageIndex{7}\): Ordering of Digits Under Different Conditions

Considera solo los dígitos 1, 2, 3, 4 y 5.

1. ¿Cuántos números de tres dígitos se pueden formar si no se puede producir repetición de dígitos?
2. ¿Cuántos números de tres dígitos se pueden formar si se permite la repetición de dígitos?
3. ¿Cuántos números de tres dígitos se pueden formar si solo se permite la repetición no consecutiva de dígitos?

Soluciones a (a): Solución 1: Usar la regla de los productos. Tenemos cualquiera de cinco opciones para el dígito uno, cualquiera de cuatro opciones para el dígito dos y tres opciones para el dígito tres. De ahí que se puedan formar\(5 \cdot 4 \cdot 3 = 60\) diferentes números de tres dígitos.

Solución 2; Usando la fórmula de permutación. Queremos que el número total de permutaciones de cinco dígitos tomados tres a la vez:

\ begin {ecuación*} P (5,3) =\ frac {5!} {(5-3)!} =5\ cdot 4\ cdot 3 = 60\ texto {.} \ end {ecuación*}

Solución a (b): La definición de permutación indica “... no hay dos elementos en cada lista iguales”. De ahí que no se pueda utilizar la fórmula de permutación. No obstante, la regla de los productos sigue aplicándose. Tenemos cualquiera de cinco opciones para el primer dígito, cinco opciones para el segundo y cinco para el tercero. Por lo que hay\(5 \cdot 5\cdot 5 = 125\) posibles diferentes números de tres dígitos si se permite la repetición.

Solución a (c): Nuevamente, aquí se aplica la regla de los productos. Tenemos cualquiera de cinco opciones para el primer dígito, pero luego para los siguientes dos dígitos tenemos cuatro opciones ya que no se nos permite repetir el dígito anterior Así que hay\(5 \cdot 4\cdot 4 = 80\) posibles números diferentes de tres dígitos si solo se permiten repeticiones no consecutivas.

Ejercicios

Ejercicio\(\PageIndex{1}\)

Si una rifa tiene tres premios diferentes y se venden mil boletos de rifa, ¿de cuántas formas diferentes se pueden distribuir los premios?

Contestar

\(P(1000,3)\)

Ejercicio\(\PageIndex{2}\)

1. ¿Cuántos números de tres dígitos se pueden formar a partir de los dígitos 1, 2, 3 si no se permite la repetición de dígitos? Enumere los números de tres dígitos.
2. ¿Cuántos números de dos dígitos se pueden formar si no se permite la repetición de dígitos? Enumerarlos.
3. ¿Cuántos números de dos dígitos se pueden obtener si se permite la repetición?

Ejercicio\(\PageIndex{3}\)

¿Cuántas palabras de ocho letras se pueden formar a partir de las 26 letras del alfabeto? Aun sin importarnos sobre si las palabras tienen sentido, hay dos interpretaciones de este problema. Responde a ambos.

Contestar

Con repetición:\(26^8\approx 2.0883\times 10^{11}\)

Sin repetición:\(P(26,8) \approx 6.2991\ 10^{10}\)

Ejercicio\(\PageIndex{4}\)

Dejar\(A\) ser un conjunto con\(\lvert A \rvert = n \text{.}\) Determinar

1. \(\displaystyle \lvert A^3 \rvert \)
2. \(\displaystyle \lvert \{ (a, b, c) \mid a, b, c \in A \textrm{ and each coordinate is different}\} \rvert \)

Ejercicio\(\PageIndex{5}\)

La final estatal de un encuentro de pista de secundaria involucra a quince escuelas. ¿De cuántas formas se pueden enumerar estas escuelas en el programa?

Contestar

\(15!\)

Ejercicio\(\PageIndex{6}\)

Considere los números de tres dígitos que se pueden formar a partir de los dígitos\(1\)\(2\)\(3\),\(4\),, y\(5\) sin repetición de dígitos permitida.

1. ¿Cuántos de estos son números pares?
2. ¿Cuántos son mayores que 250?

Ejercicio\(\PageIndex{7}\)

Los 15 jugadores del equipo de básquetbol Tall U. son capaces de jugar cualquier posición.

1. ¿De cuántas maneras puede el entrenador en Tall U. llenar los cinco puestos iniciales en un juego?
2. ¿Cuál es la respuesta si el centro debe ser uno de dos jugadores?

Contestar

1. \(\displaystyle P(15,5)=360360\)
2. \(\displaystyle 2\cdot 14\cdot 13\cdot 12\cdot 11=48048\)

Ejercicio\(\PageIndex{8}\)

1. ¿De cuántas maneras puede un jardinero plantar cinco especies diferentes de arbustos en un círculo?
2. ¿Cuál es la respuesta si dos de los arbustos son iguales?
3. ¿Cuál es la respuesta si todos los arbustos son idénticos?

Ejercicio\(\PageIndex{9}\)

El presidente del Club de Matemáticas e Informática quisiera concertar una reunión con seis asistentes, incluido el mandatario. Habrá tres especializaciones en ciencias de la computación y tres de matemáticas en la reunión. ¿De cuántas maneras pueden sentarse las seis personas en una mesa circular si el mandatario no quiere que personas con las mismas especializaciones se sienten una al lado de la otra?

Contestar

\(2\cdot P(3,3)=12\)

Ejercicio\(\PageIndex{10}\)

Seis personas solicitan tres empleos idénticos y todas están calificadas para los puestos. Dos trabajarán en Nueva York y el otro trabajará en San Diego. ¿De cuántas formas se pueden cubrir los puestos?

Ejercicio\(\PageIndex{11}\)

Vamos\(A = \{1, 2, 3, 4\} \text{.}\) Determinar la cardinalidad de

1. \(\displaystyle \{ (a_1,a_2) \mid a_1 \neq a_2 \}\)
2. Cuál es la respuesta a la parte anterior si\(\lvert A \rvert = n\)
3. Si se\(\lvert A \rvert =n\text{,}\) determina el número de\(m\) -tuplas en\(A\text{,}\)\(m \leq n\text{,}\) donde cada coordenada es diferente de las otras coordenadas.

Contestar

1. \(P(4,2)=12\)
2. \(P(n;2)=n(n-1)\)
3. Caso 1:\(m>n\). Dado que las coordenadas deben ser diferentes, este caso es imposible.
   Caso 2:\(m\leq n\). \(P(n;m)\).