3.6: Proposiciones sobre un Universo

Proposiciones sobre un universo

Considera la frase “Era miembro de los Medias Rojas de Boston”. No hay manera de que podamos asignar un valor de verdad a esta frase a menos que se especifique “él”. Por esa razón, no lo consideraríamos una proposición. No obstante, “él” puede considerarse una variable que ocupa un lugar para cualquier nombre. Podríamos querer restringir el valor de “él” a todos los nombres en los libros de récords de béisbol de las Grandes Ligas. Si ese es el caso, decimos que la sentencia es una proposición sobre el conjunto de jugadores de béisbol de Grandes Ligas, pasados y presentes.

Definición\(\PageIndex{1}\): Proposition over a Universe

Dejar\(U\) ser un conjunto no vacío. Una proposición sobre\(U\) es una oración que contiene una variable que puede tomar cualquier valor en\(U\) y que tiene un valor de verdad definido como resultado de tal sustitución.

Ejemplo\(\PageIndex{1}\): Some Propositions over a Variety of Universes

1. Algunas proposiciones sobre los enteros son\(4x^2 - 3x = 0\text{,}\)\(0 \leq n \leq 5\text{,}\) y “\(k\)es un múltiplo de 3”.
2. Algunas proposiciones sobre los números racionales son\(4x^2 - 3x = 0\text{,}\)\(y^2=2\text{,}\) y\((s - 1)(s + 1) = s^2 - 1\text{.}\)
3. Algunas proposiciones sobre los subconjuntos de\(\mathbb{P}\) son\((A =\emptyset ) \lor (A = \mathbb{P} )\text{,}\)\(3 \in A\text{,}\) y\(A \cap \{1, 2, 3\}\neq \emptyset\text{.}\)

Todas las leyes de la lógica que enumeramos en la Sección 3.4 son válidas para proposiciones sobre un universo. Por ejemplo, si\(p\) y\(q\) son proposiciones sobre los enteros, podemos estar seguros de que\(p \land q \Rightarrow p\text{,}\) porque\((p \land q) \to p\) es una tautología y es verdadera sin importar en qué valores se den las variables\(p\) y\(q\) se den. Si especificamos\(p\) y\(q\) ser\(p(n) : n < 4\) y también\(q(n) : n < 8\text{,}\) podemos decir que eso\(p\) implica\(p \land q\text{.}\) Esto no es una implicación habitual, sino para las proposiciones que se están discutiendo, es verdad. Una manera de describir esta situación en general es con conjuntos de verdad.

Conjuntos de verdad

Definición \(\PageIndex{2}\): Truth Set

Si\(p\) es una proposición sobre\(U\text{,}\) el conjunto de verdad\(p\) es\(T_p = \{a \in U \mid p(a) \textrm{ is true}\}\text{.}\)

Ejemplo\(\PageIndex{2}\): Truth Set Example

El conjunto de verdad de la proposición\(\{1, 2\} \cap A = \emptyset\text{,}\) tomada como una proposición sobre el conjunto de poder de\(\{1, 2, 3, 4\}\) es\(\{\emptyset , \{3\}, \{4\}, \{3, 4\}\}\text{.}\)

Ejemplo\(\PageIndex{3}\): Truth Sets Depend on the Universe

Sobre el universo\(\mathbb{Z}\) (los enteros), el conjunto de verdad de\(4x^2- 3x = 0\) es\(\{0\}\text{.}\) Si el universo se expande a los números racionales, el conjunto de verdad se convierte\(\{0, 3/4\}\text{.}\) El término conjunto de soluciones se usa a menudo para el conjunto de verdad de una ecuación como la de este ejemplo.

Definición\(\PageIndex{3}\): Tautologies and Contradictions over a Universe

Una proposición sobre\(U\) es una tautología si su conjunto de verdad es\(U\text{.}\) Es una contradicción si su conjunto de verdad está vacío.

Ejemplo\(\PageIndex{4}\): Tautology, Contradiction over \(\mathbb{Q}\)

\((s - 1)(s + 1) = s^2 - 1\)es una tautología sobre los números racionales. \(x^2-2 = 0\)es una contradicción sobre los racionales.

Los conjuntos de verdad de proposiciones compuestas se pueden expresar en términos de los conjuntos de verdad de proposiciones simples. Por ejemplo,\(a \in T_{p\land q}\) si y sólo si\(a\) hace\(p \land q\) verdad. Esto es cierto si y solo si\(a\) hace ambos\(p\) y\(q\) verdadero, lo cual, a su vez, es cierto si y solo si\(a \in T_p\cap T_q\text{.}\) Esto explica por qué el conjunto de verdad de la conjunción de dos proposiciones equivale a la intersección de los conjuntos de verdad de las dos proposiciones. La siguiente lista resume la conexión entre conjuntos de verdad compuestos y simples

Tabla\(\PageIndex{1}\): Conjuntos de verdad de declaraciones compuestas

\(T_{p\land q}=T_p\cap T_q\)

\(T_{p\lor q}=T_p\cup T_q\)

\(T_{\neg p}=T_p{}^c\)

\(T_{p\leftrightarrow q}=\left(T_p\cap T_q\right)\cup \left(T_p{}^c\cap T_q{}^c\right)\)

\(T_{p\to q}=T_p{}^c\cup T_q\)

Definición\(\PageIndex{4}\): Equivalence of Propositions over a Universe

Dos proposiciones,\(p\) y\(q\text{,}\) son equivalentes si\(p \leftrightarrow q\) es una tautología. En cuanto a conjuntos de verdad, esto significa eso\(p\) y\(q\) son equivalentes si\(T_p=T_q\).

Ejemplo\(\PageIndex{5}\): Some Pairs of Equivalent Propositions

1. \(n + 4 = 9\)y\(n = 5\) son proposiciones equivalentes sobre los enteros.
2. \(A \cap \{4\} \neq \emptyset\)y\(4 \in A\) son proposiciones equivalentes sobre el conjunto de potencias de los números naturales.

Definición\(\PageIndex{5}\): Implication for Propositions over a Universe

Si\(p\) y\(q\) son proposiciones sobre\(U\text{,}\)\(p\) implica\(q\) si\(p \rightarrow q\) es una tautología.

Dado que el conjunto de verdad\(p \rightarrow q\) es\(T_p{}^c\cup T_q\text{,}\) el diagrama de Venn para\(T_{p\to q}\) en la Figura\(\PageIndex{1}\) muestra que\(p \Rightarrow q\) cuando\(T_p\subseteq T_q\text{.}\)

Figura Diagrama de\(\PageIndex{1}\): Venn para\(T_{p\to q}\)

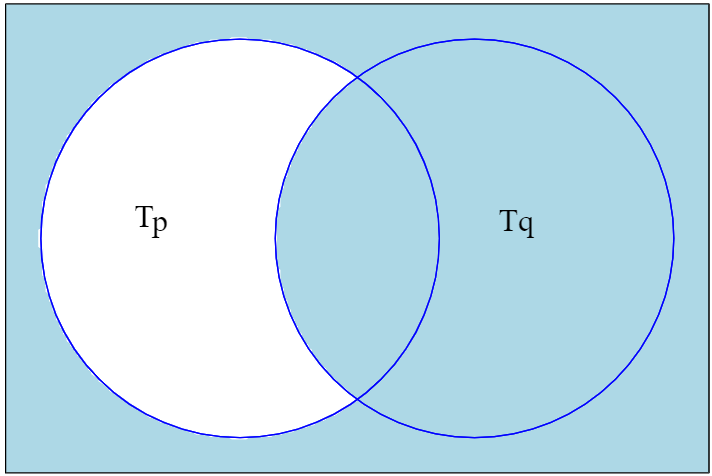
Ejemplo\(\PageIndex{6}\): Examples of Implications

1. Sobre los números naturales:\(n \leq 4 \Rightarrow n \leq 8\) desde\(\{0, 1, 2, 3, 4\} \subseteq \{0, 1, 2, 3, 4, 5, 6, 7, 8\}\)
2. Sobre el conjunto de potencias de los enteros:\(\lvert A^c \rvert=1\) implica\(A\cap \{0,1\}\neq \emptyset\)
3. Sobre el conjunto de potencia de los enteros,\(A \subseteq \textrm{ even integers } \Rightarrow A\cap \textrm{ odd integers } =\emptyset\)

Ejercicios

Ejercicio\(\PageIndex{1}\)

Si\(U = \mathcal{P}( \{1, 2, 3, 4\})\text{,}\) ¿cuáles son los conjuntos de verdad de las siguientes proposiciones?

1. \(A \cap \{2, 4\} = \emptyset\text{.}\)
2. \(3 \in A\)y\(1 \notin A\text{.}\)
3. \(A \cup \{1\} = A\text{.}\)
4. \(A\)es un subconjunto apropiado de\(\{2, 3, 4\}\text{.}\)
5. \(\lvert A \rvert=\lvert A^c \rvert\text{.}\)

Contestar

1. \(\displaystyle \{\{1\},\{3\},\{1,3\},\emptyset\}\)
2. \(\displaystyle \{\{3\}, \{3,4\}, \{3,2\}, \{2,3,4\}\}\)
3. \(\displaystyle \{\{1\}, \{1,2\}, \{1,3\}, \{1,4\}, \{1,2,3\}, \{1,2,4\}, \{1,3,4\}, \{1,2,3,4\}\}\)
4. \(\displaystyle \{\{2\}, \{3\}, \{4\}, \{2,3\}, \{2,4\}, \{3,4\}\}\)
5. \(\displaystyle \{A\subseteq U:\left| A\right| =2\}\)

Ejercicio\(\PageIndex{2}\)

Sobre el universo de enteros positivos, definir

Mesa\(\PageIndex{2}\)

\(p(n)\text{:}\)	\(n\)es prime y\(n < 32\text{.}\)
\(q(n)\text{:}\)	\(n\)es un poder de 3.
\(r(n)\text{:}\)	\(n\)es un divisor de 27.

1. ¿Cuáles son los conjuntos de verdad de estas proposiciones?
2. ¿Cuál de las tres proposiciones implica una de las otras?

Contestar

1. 1. \(\displaystyle T_p = \{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 \}\)
   2. \(\displaystyle T_q = \{1, 3, 9, 27, 81, \dots \}\)
   3. \(\displaystyle T_r = \{1, 3, 9, 27 \}\)
2. \(\displaystyle r \Rightarrow q \)

Ejercicio\(\PageIndex{3}\)

Si\(U = \{0, 1, 2\}\text{,}\) ¿cuántas proposiciones más\(U\) podrías enumerar sin enumerar dos que sean equivalentes?

Contestar

Hay\(2^3=8\) subconjuntos\(U\text{,}\) que permiten la posibilidad de proposiciones\(2^8\) no equivalentes sobre\(U\text{.}\)

Ejercicio\(\PageIndex{4}\)

Dadas las proposiciones sobre los números naturales:

Mesa\(\PageIndex{3}\)

\(p : n < 4\text{,}\)

\(q : 2n > 17\text{,}\)y

\(r : n \textrm{ is a divisor of } 18\)

¿Cuáles son los conjuntos de verdad de:

1. \(\displaystyle q\)
2. \(\displaystyle p\land q\)
3. \(\displaystyle r\)
4. \(\displaystyle q\to r\)

Ejercicio\(\PageIndex{5}\)

Supongamos que\(s\) es una proposición sobre\(\{1, 2,\dots, 8\}\text{.}\) Si\(T_s = \{1, 3, 5, 7\}\text{,}\) da dos ejemplos de proposiciones que son equivalentes a\(s\text{.}\)

Contestar

Dos respuestas posibles:\(s\) es impar y\((s-1)(s-3)(s-5)(s-7)=0\)

Ejercicio\(\PageIndex{6}\)

1. Determinar los conjuntos de verdad de las siguientes proposiciones sobre los enteros positivos:

\ begin {ecuación*} p (n): n\ textrm {es un cuadrado perfecto y} n < 100\ end {ecuación*}

\ begin {ecuación*} q (n): n =\ lvert\ mathcal {P} (A)\ rvert\ textrm {para algún conjunto} A\ text {.} \ end {ecuación*}

2. Determinar\(T_{p\land q}\) para\(p\) y\(q\) por encima.

Ejercicio\(\PageIndex{7}\)

Que el universo sea\(\mathbb{Z}\text{,}\) el conjunto de enteros. ¿Cuál de las siguientes proposiciones es equivalente sobre\(\mathbb{Z}\text{?}\)

Mesa\(\PageIndex{4}\)

\(a\text{:}\)	\(0 < n^2 < 9\)
\(b\text{:}\)	\(0 < n^3 < 27\)
\(c\text{:}\)	\(0 < n < 3\)

Contestar

\(b\)y\(c\)