3.5: Sistemas matemáticos y pruebas

Sistemas matemáticos

En esta sección, presentamos una visión general de qué es un sistema matemático y cómo la lógica juega un papel importante en uno. El método axiomático que usaremos aquí no se duplicará con tanta formalidad en ningún otro lugar del libro, sino que esperamos que un énfasis en cómo se desarrollan y organizan los hechos matemáticos ayude a unificar los conceptos que presentaremos. El sistema de proposiciones y operadores lógicos que hemos desarrollado servirá de modelo para nuestra discusión. En términos generales, un sistema matemático se puede definir de la siguiente manera.

Definición\(\PageIndex{1}\): Mathematical System

Un sistema matemático consiste en:

1. Un conjunto o universo,\(U\text{.}\)
2. Definiciones: oraciones que explican el significado de conceptos que se relacionan con el universo. Se dice que cualquier término utilizado para describir el universo mismo es indefinido. Todas las definiciones se dan en términos de estos conceptos indefinidos de objetos.
3. Axiomas: aseveraciones sobre las propiedades del universo y reglas para crear y justificar más aserciones. Estas reglas incluyen siempre el sistema de lógica que hemos desarrollado hasta este punto.
4. Teoremas: las aseveraciones adicionales mencionadas anteriormente.

Ejemplo\(\PageIndex{1}\): Euclidean Geometry

En la geometría euclidiana el universo consta de puntos y líneas (dos términos indefinidos). Entre las definiciones se encuentra una definición de líneas paralelas y entre los axiomas está el axioma que dos líneas paralelas distintas nunca encuentran.

Ejemplo\(\PageIndex{2}\): Propositional Calculus

El cálculo proposicional es un nombre formal para el sistema lógico que hemos estado discutiendo. El universo consiste en proposiciones. Los axiomas son las tablas de verdad para los operadores lógicos y las definiciones clave son las de equivalencia e implicación. Usamos proposiciones para describir cualquier otro sistema matemático; por lo tanto, esta es la cantidad mínima de estructura que puede tener un sistema matemático.

Definición\(\PageIndex{2}\): Theorem

Una verdadera proposición derivada de los axiomas de un sistema matemático se llama teorema.

Los teoremas se expresan normalmente en términos de un número finito de proposiciones\(p_1, p_2, . . . ,p_n\),, llamadas premisas, y una proposición,\(C\text{,}\) llamada conclusión. Estos teoremas toman la forma

\ begin {ecuation*} p_1\ land p_2\ land\ cdots\ land p_n\ Rightarrow C\ end {ecuación*}

o de manera más oficiosa,

\ begin {ecuación*} p_1, p_2,..,\ textrm {y} p_n\ textrm {implica} C\ final {ecuación*}

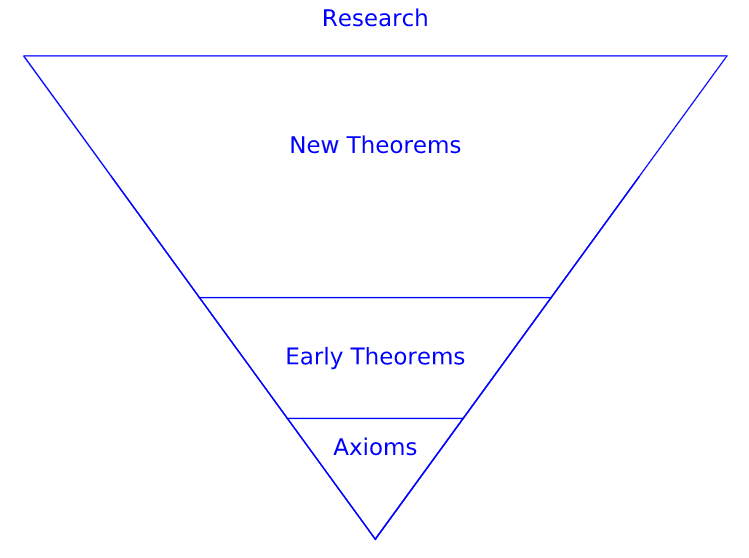
Para un teorema de este tipo, decimos que las premisas implican la conclusión. Cuando se afirma un teorema, se supone que los axiomas del sistema son ciertos. Además, cualquier teorema previamente probado puede considerarse una extensión de los axiomas y puede ser utilizado para demostrar que el nuevo teorema es cierto. Cuando la prueba está completa, el nuevo teorema puede ser utilizado para probar teoremas posteriores. Un sistema matemático se puede visualizar como una pirámide invertida con los axiomas en la base y los teoremas expandiéndose en varias direcciones.

Figura\(\PageIndex{1}\): El cuerpo de conocimiento en un sistema matemático

Definición\(\PageIndex{3}\): Proof

Una prueba de un teorema es una secuencia finita de pasos lógicamente válidos que demuestran que las premisas de un teorema implican su conclusión.

Exactamente lo que constituye una prueba no siempre está claro. Por ejemplo, un matemático de investigación podría requerir solo unos pocos pasos para demostrar un teorema a un colega, pero podría tomar una hora para dar una prueba efectiva a una clase de estudiantes. Por lo tanto, lo que constituye una prueba a menudo depende de la audiencia. Pero el público no es el único factor. Uno de los teoremas más famosos de la teoría gráfica, El teorema de los cuatro colores, Teorema 9.6.1, fue probado en 1976, después de más de un siglo de esfuerzo por muchos matemáticos. Parte de la prueba consistió en que una computadora verificara muchas gráficas diferentes para una determinada propiedad. Sin la ayuda de la computadora, esta comprobación habría llevado años. A los ojos de algunos matemáticos, esta prueba se consideró cuestionable. Pruebas más cortas se han desarrollado desde 1976 y no hay controversia asociada con El Teorema de los Cuatro Colores en este momento.

Prueba Directa

Teóricamente, se puede probar cualquier cosa en el cálculo proposicional con tablas de verdad. De hecho, las leyes de la lógica enunciadas en la Sección 3.4 son todas teoremas. El cálculo proposicional es uno de los pocos sistemas matemáticos para los que cualquier oración válida puede determinarse verdadera o falsa por medios mecánicos. Un programa para escribir tablas de verdad no es demasiado difícil de escribir; sin embargo, lo que se puede hacer teóricamente no siempre es práctico. Por ejemplo,

\ comenzar {ecuación*} a, a\ a b, b\ a c,.. , y\ a z\ Rightarrow z\ end {ecuación*}

es un teorema en el cálculo proposicional. Sin embargo, supongamos que usted escribió un programa así y lo hizo escribir la tabla de la verdad para

\ comenzar {ecuación*} (a\ tierra (a\ a b)\ tierra (b\ a c)\ tierra\ cdots\ tierra (y\ a z))\ a z\ fin {ecuación*}

La tabla de la verdad tendrá\(2^{26}\) casos. A un millón de casos por segundo, tardaría aproximadamente una hora en verificar el teorema. Ahora bien, si decidiste comprobar un teorema similar,

\ begin {ecuación*} p_1, p_1\ a p_2,\ ldots, p_ {99}\ a p_ {100}\ fila derecha p_ {100}\ fin {ecuación*}

realmente tendrías problemas de tiempo. Habría\(2^{100} \approx 1.26765\times 10^{30}\) casos para comprobar en la tabla de la verdad. A un millón de casos por segundo tardaría aproximadamente\(1.46719\times 10^{19}\) días en verificar todos los casos. Para la mayor parte del resto de esta sección, discutiremos un método alternativo para probar teoremas en el cálculo proposicional. Es el mismo método que usaremos de una manera menos formal para las pruebas en otros sistemas. Los métodos axiomáticos formales serían demasiado difíciles de manejar para usarlos realmente en secciones posteriores. Sin embargo, ninguno de los teoremas de capítulos posteriores se declararía si no pudieran ser probados por el método axiomático.

Presentaremos aquí dos tipos de pruebas, directas e indirectas.

Ejemplo\(\PageIndex{3}\): A Typical Direct Proof

Este es un teorema:\(p \rightarrow r, q\rightarrow s,p\lor q\Rightarrow s\lor r\text{.}\) Una prueba directa de este teorema es:

Tabla\(\PageIndex{1}\): Prrof directo de\(p\rightarrow r\),\(q\rightarrow s\),\(p\lor q\Rightarrow s\lor r\)

Paso	Proposición	Justificación
1.	\(p\lor q\)	Premisa
2.	\(\neg p\to q\)	(1), regla condicional
3.	\(q\to s\)	Premisa
4.	\(\neg p\to s\)	(2), (3), regla de cadena
5.	\(\neg s\to p\)	(4), contrapositivo
6.	\(p\to r\)	Premisa
7.	\(\neg s\to r\)	(5), (6), regla de cadena
8.	\(s\lor r\)	(7), regla condicional\(\square\)

Tenga en cuenta que\(\square\) marca el final de una prueba.

Ejemplo\(\PageIndex{3}\) ilustra el método habitual de prueba formal en un sistema matemático formal. Las reglas que rigen estas pruebas son:

1. Una prueba debe terminar en un número finito de pasos.
2. Cada paso debe ser ya sea una premisa o una proposición que se implique de pasos anteriores utilizando cualquier equivalencia o implicación válida.
3. Para una prueba directa, el último paso debe ser la conclusión del teorema. Para una prueba indirecta (ver abajo), el último paso debe ser la contradicción.
4. Columna de Justificación. La columna etiquetada como “justificación” es análoga a los comentarios que aparecen en la mayoría de los buenos programas de computadora. Simplemente hacen que la prueba sea más legible.

Ejemplo\(\PageIndex{4}\): Two Proofs of the Same Theorem

Aquí hay dos pruebas directas de\(\neg p \lor q, s\lor p, \neg q \Rightarrow s\text{:}\)

Tabla\(\PageIndex{2}\): Prueba directa de\(\neg p\lor q\),\(s\lor p\),\(\neg q\Rightarrow s\)

1.	\(\neg p\lor q\)	Premisa
2.	\(\neg q\)	Premisa
3.	\(\neg p\)	Simplificación disyuntiva, (1), (2)
4.	\(s\lor p\)	Premisa
5.	\(s\)	Simplificación disyuntiva, (3), (4),\(\square\)

Se le invita a justificar los pasos en esta segunda prueba:

Tabla\(\PageIndex{3}\): Prueba alterna de\(\neg p\lor q\),\(s\lor p\),\(\neg q\Rightarrow s\)

1.	\(\neg p \lor q\)
2.	\(\neg q \rightarrow \neg p\)
3.	\(s\lor p\)
4.	\(p \lor s\)
5.	\(\neg p \to s\)
6.	\(\neg q \rightarrow s\)
7.	\(\neg q\)
8.	\(s\)\(\square\)

La conclusión de un teorema suele ser una proposición condicional. La condición de la conclusión se puede incluir como premisa en la prueba del teorema. El objeto de la prueba es entonces probar la consecuencia de la conclusión. Esta regla se justifica por la ley lógica

\ comenzar {ecuación*} p\ fila derecha (h\ fila derecha c)\ Izquierda fila (p\ tierra h)\ fila derecha c\ final {ecuación*}

Ejemplo\(\PageIndex{5}\): Example of a Proof with a Conditional Conclusion

La siguiente prueba de\(p \to (q \rightarrow s), \neg r \lor p, q \Rightarrow r \rightarrow s\) incluye\(r\) como cuarta premisa. Inferencia de verdad de\(s\) completa la prueba.

Tabla\(\PageIndex{4}\): Prueba de un teorema con una conclusión condicional.

1.	\(\neg r\lor p\)	Premisa
2.	\(r\)	Premisa agregada
3.	\(p\)	(1), (2), simplificación de la disyunción
4.	\(p\to (q\to s)\)	Premisa
5.	\(q\to s\)	(3), (4), desprendimiento
6.	\(q\)	Premisa
7.	\(s\)	(5), (6), desprendimiento. \(\square\)

Prueba indirecta

Consideremos un teorema\(P\Rightarrow C\text{,}\) donde\(P\) representa\(p_1, p_2, . . . , \textrm{ and } p_n\text{,}\) las premisas. El método de prueba indirecta se basa en la equivalencia\(P\rightarrow C\Leftrightarrow \neg (P\land \neg C)\text{.}\) En palabras, esta ley lógica establece que si\(P \Rightarrow C\text{,}\) entonces siempre\(P \land \neg C\) es falsa; es decir,\(P \land \neg C\) es una contradicción. Esto significa que un método válido de prueba es negar la conclusión de un teorema y agregar esta negación a las premisas. Si se puede dar a entender una contradicción de este conjunto de proposiciones, la prueba es completa. Para las pruebas de esta sección, una contradicción a menudo tomará la forma\(t \land \neg t\text{.}\)

Para pruebas que involucren números, una contradicción podría ser\(1 = 0\) o pruebas\(0 < 0\text{.}\) indirectas que involucren conjuntos podrían concluir con\(x \in \emptyset\) o (\(x \in A\)y\(x \in A^c\)). Las pruebas indirectas suelen ser más convenientes que las pruebas directas en ciertas situaciones. Las pruebas indirectas a menudo se llaman pruebas por contradicción.

Ejemplo\(\PageIndex{6}\): An Indirect Proof

Aquí hay un ejemplo de una prueba indirecta del teorema en Ejemplo\(\PageIndex{3}\).

Tabla\(\PageIndex{5}\): Una prueba indirecta de\(p\to r\)\(q\to s\),\(p\lor q\Rightarrow s\lor r\)

1.	\(\neg (s\lor r)\)	Conclusión negada
2.	\(\neg s\land \neg r\)	Ley de DeMorgan, (1)
3.	\(\neg s\)	Simplificación conjuntiva, (2)
4.	\(q\to s\)	Premisa
5.	\(\neg q\)	Razonamiento indirecto, (3), (4)
6.	\(\neg r\)	Simplificación conjuntiva, (2)
7.	\(p\to r\)	Premisa
8.	\(\neg p\)	Razonamiento indirecto, (6), (7)
9.	\((\neg p)\land (\neg q)\)	Conjuntiva, (5), (8)
10.	\(\neg (p\lor q)\)	Ley de DeMorgan, (9)
11.	\(p\lor q\)	Premisa
12.	\(0\)	(10), (11)\(\square\)

Nota\(\PageIndex{1}\): Proof Style

Las reglas permiten enumerar las premisas de un teorema de inmediato; sin embargo, una prueba es mucho más fácil de seguir si las premisas solo se listan cuando son necesarias.

Ejemplo\(\PageIndex{7}\): Yet Another Indirect Proof

Aquí hay una prueba indirecta de\(a \rightarrow b, \neg (b \lor c ) \Rightarrow \neg a\text{.}\)

Tabla\(\PageIndex{6}\): Prueba indirecta de\(a\to b\),\(\neg (b\lor c)\Rightarrow \neg a\)

1.	\(a\)	Negación de la conclusión
2.	\(a\to b\)	Premisa
3.	\(b\)	(1), (2), desprendimiento
4.	\(b\lor c\)	(3), adición disyuntiva
5.	\(\neg (b\lor c)\)	Premisa
6.	\(0\)	(4), (5)\(\square\)

Como mencionamos al inicio de esta sección, sólo estamos presentando una visión general de lo que es un sistema matemático. Para mayor detalle sobre las teorías axiomáticas, véase Stoll (1961). Una excelente descripción de cómo el cálculo proposicional juega un papel en la inteligencia artificial está contenida en Hofstadter (1980). Si te gusta el reto de construir pruebas en el cálculo proposicional, deberías disfrutar del juego WFF'N PROOF (1962), de L.E. Allen.

Ejercicios

Ejercicio\(\PageIndex{1}\)

Demostrar con tablas de verdad:

1. \(\displaystyle p\lor q, \neg q\Rightarrow p\)
2. \(\displaystyle p \rightarrow q, \neg q \Rightarrow \neg p\)

Responder

1. \ begin {ecuation*}\ begin {array} {cccc} p & q & (p\ lor q)\ land\ neg q & ((p\ lor q)\ land\ neg q)\ a p\\ 0 & 0 & 0 & 1\\ 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 1\\ 1 & 1 & 0 & 0 & 1\\ end array}\ fin {ecuación*}
2. \ begin {ecuación*}\ begin {array} {ccccc} p & q & (p\ a q)\ land\ neg q &\ neg p & (p\ a q)\ land (\ neg q)\\ 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 & 0 & 1 & 1 & 1\\ 1 & 0 & 0 & 0 & 0 & 1\\\ end {array}\ end {ecuación*}

Ejercicio\(\PageIndex{2}\)

Demostrar con tablas de verdad:

1. \(\displaystyle q, \neg q\Rightarrow p\)
2. \(\displaystyle p \rightarrow q \Rightarrow \neg p \lor q\)

Ejercicio\(\PageIndex{3}\)

Dar pruebas directas e indirectas de:

1. \(a \rightarrow b, c \rightarrow b, d\rightarrow (a \lor c), d\Rightarrow b\text{.}\)
2. \((p\to q) \land (r\to s), (q\rightarrow t) \land (s \to u), \neg (t \land u), p \rightarrow r \Rightarrow \neg p\text{.}\)
3. \(p\to (q\to r),\neg s \lor p,q\Rightarrow s\to r\text{.}\)
4. \(p\rightarrow q, q\rightarrow r, \neg (p \land r), p \lor r \Rightarrow r\text{.}\)
5. \(\displaystyle \neg q, p\to q, p\lor t \Rightarrow t\)

Responder

1. Prueba directa:
   1. \(\neg b\quad \)Conclusión negada
   2. \(a\to b\quad \)Premisa
   3. \(\neg a\quad \)Razonamiento Indirecto (1), (2)
   4. \(c\to b\quad \)Premisa
   5. \(\neg c\quad \)Razonamiento Indirecto (1), (4)
   6. \((\neg a\land \neg c)\quad \)Conjuntiva (3), (5)
   7. \(\neg (a\lor c)\quad \)Ley de DeMorgan (6)
   8. \(d\to (a\lor c)\quad \)Premisa
   9. \(\neg d\quad \)Razonamiento Indirecto (7), (8)
   10. \(d\quad \)Premisa
   11. \(\mathbb{0} \quad \)(9), (10)\(\quad \square\)

1. Prueba indirecta:
   1. \(\displaystyle d\to (a\lor c)\)
   2. \(\displaystyle d\)
   3. \(\displaystyle a\lor c\)
   4. \(\displaystyle a\to b\)
   5. \(\displaystyle \neg a \lor b\)
   6. \(\displaystyle c\to b\)
   7. \(\displaystyle \neg c\lor b\)
   8. \(\displaystyle (\neg a\lor b)\land (\neg c\lor b)\)
   9. \(\displaystyle (\neg a\land \neg c) \lor b\)
   10. \(\displaystyle \neg (a\lor c)\lor b\)
   11. \(b\)\(\square\)

2. Prueba directa:
   1. \(\displaystyle (p\to q)\land (r\to s)\)
   2. \(\displaystyle p\to q\)
   3. \(\displaystyle (p\to t)\land (s\to u)\)
   4. \(\displaystyle q\to t\)
   5. \(\displaystyle p\to t\)
   6. \(\displaystyle r\to s\)
   7. \(\displaystyle s\to u\)
   8. \(\displaystyle r\to u\)
   9. \(\displaystyle p\to r\)
   10. \(\displaystyle p\to u\)
   11. \(p\to (t\land u)\)Uso\((x\to y)\land (x\to z)\Leftrightarrow x\to (y\land z)\)
   12. \(\displaystyle \neg (t\land u)\to \neg p\)
   13. \(\displaystyle \neg (t\land u)\)
   14. \(\neg p\)\(\quad \square\)

2. Prueba indirecta:
   1. \(\displaystyle p\)
   2. \(\displaystyle p\to q\)
   3. \(\displaystyle q\)
   4. \(\displaystyle q\to t\)
   5. \(\displaystyle t\)
   6. \(\displaystyle \neg (t\land u)\)
   7. \(\displaystyle \neg t\lor \neg u\)
   8. \(\displaystyle \neg u\)
   9. \(\displaystyle s\to u\)
   10. \(\displaystyle \neg s\)
   11. \(\displaystyle r\to s\)
   12. \(\displaystyle \neg r\)
   13. \(\displaystyle p\to r\)
   14. \(\displaystyle r\)
   15. \(0\)\(\quad \square\)

3. Prueba directa:
   1. \(\neg s\lor p\quad \)Premisa
   2. \(s\quad \)Premisa añadida (conclusión condicional)
   3. \(\neg (\neg s)\quad \)Involución (2)
   4. \(p \quad \)Simplificación disyuntiva (1), (3)
   5. \(p\to (q\to r)\quad \)Premisa
   6. \(q\to r\quad \)Desprendimiento (4), (5)
   7. \(q \quad\)Premisa
   8. \(r\quad \)Desprendimiento (6), (7)\(\square\)

3. Prueba indirecta:
   1. \(\neg (s\to r)\quad \)Conclusión negada
   2. \(\neg (\neg s\lor r)\quad \)Equivalencia condicional (I)
   3. \(s\land \neg r\quad \)DeMorgan (2)
   4. \(s\quad\)Simplificación conjuntiva (3)
   5. \(\neg s\lor p\quad \)Premisa
   6. \(s\to p\quad\)Equivalencia condicional (5)
   7. \(p \quad\)Desprendimiento (4), (6)
   8. \(p\to (q\to r)\quad\)Premisa
   9. \(q\to r \quad\)Desprendimiento (7), (8)
   10. \(q\quad \)Premisa
   11. \(r\quad\)Desprendimiento (9), (10)
   12. \(\neg r \quad\)Simplificación conjuntiva (3)
   13. \(0 \quad\)Conjunción (11), (12)\(\square\)

4. Prueba directa:
   1. \(\displaystyle p\to q\)
   2. \(\displaystyle q\to r\)
   3. \(\displaystyle p\to r\)
   4. \(\displaystyle p\lor r\)
   5. \(\displaystyle \neg p\lor r\)
   6. \(\displaystyle (p\lor r)\land (\neg p\lor r)\)
   7. \(\displaystyle (p\land \neg p)\lor r\)
   8. \(\displaystyle 0\lor r\)
   9. \(r\)\(\square\)

4. Prueba indirecta:
   1. \(\neg rv\)Conclusión negada
   2. \(p\lor r\quad\)Premisa
   3. \(p\quad\)(1), (2)
   4. \(p\to q\quad\)Premisa
   5. \(q \quad \)Desprendimiento (3), (4)
   6. \(q\to r\quad\)Premisa
   7. \(r \quad \)Desprendimiento (5), (6)
   8. \(0 \quad\)(1), (7)\(\square\)

Ejercicio\(\PageIndex{4}\)

Dar pruebas directas e indirectas de:

1. \(p\rightarrow q, \neg r\rightarrow \neg q, \neg r \Rightarrow \neg p\text{.}\)
2. \(p\rightarrow \neg q, \neg r\rightarrow q, p \Rightarrow r\text{.}\)
3. \(a \lor b, c \land d, a \rightarrow \neg c \Rightarrow b\text{.}\)

Ejercicio\(\PageIndex{5}\)

¿Son válidos los siguientes argumentos? Si son válidas, construya pruebas formales; si no son válidas, explique por qué no.

1. Si los salarios aumentan, entonces habrá inflación. El costo de vida no aumentará si no hay inflación. Los salarios aumentarán. Por lo tanto, el costo de vida aumentará.
2. Si las carreras son fijas o los casinos están torcidos, entonces el comercio turístico disminuirá. Si el comercio turístico disminuye, entonces la policía estará contenta. El cuerpo policial nunca está contento. Por lo tanto, las carreras no son fijas.

Responder

1. \(W\)Dejemos que signifique “Los salarios\(I\) aumentarán”, signifiquen “habrá inflación” y\(C\) signifiquen “el costo de vida aumentará”. Por lo tanto el argumento es:\(W\to I,\text{ }\neg I\to \neg C,\text{ }W\Rightarrow C\text{.}\) El argumento no es válido. La manera más fácil de ver esto es a través de una tabla de la verdad, que tiene un caso, el séptimo, que esta falsa. Que\(x\) sea la conjunción de todas las premisas.
   \(\begin{array}{ccccccccc} W & I & C & \neg I & \neg C & W\to I & \neg I\to \neg C & x & x\to C \\ \hline 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 0 & 1 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 & 1 & 1 & 1 \\ \end{array}\)
2. Que\(r\) representen “las carreras son fijas”,\(c\) significa “los casinos están torcidos”\(t\), significan “el comercio turístico va a disminuir” y\(p\) representar “la policía estará feliz”. Por lo tanto, el argumento es:
   \ begin {equation*} (r\ lor c)\ to t, t\ to p,\ neg p\ to\ neg r\ text {.} \ end {equation*}
   El argumento es válido. Prueba:
   1. \(t\to p\quad \)Premisa
   2. \(\neg p\quad \)Premisa
   3. \(\neg t\quad \)Razonamiento Indirecto (1), (2)
   4. \((r\lor c)\to t\quad \)Premisa
   5. \(\neg (r\lor c)\quad \)Razonamiento Indirecto (3), (4)
   6. \((\neg r)\land (\neg c)\quad \)DeMorgan (5)
   7. \(\neg r\quad \)Simplificación de la conjunción\((6)\text{ }\square\)

Ejercicio\(\PageIndex{6}\)

Determinar la validez del siguiente argumento: Para que los estudiantes tengan un buen desempeño en un curso discreto de matemáticas, es necesario que estudien mucho. A los alumnos que les va bien en los cursos no se saltan clases. A los estudiantes que estudian duro les va bien en los cursos. Por lo tanto, los estudiantes que les va bien en un curso discreto de matemáticas no se saltan a clase

Ejercicio\(\PageIndex{7}\)

Describir cómo se\(p_1,p_1\to p_2,\ldots ,p_{99}\to p_{100}\Rightarrow p_{100}\) podría probar en 199 pasos.

Contestar

\(p_1\to p_k\)e\(p_k\to p_{k+1}\) implica\(p_1\to p_{k+1}\). Se necesitan dos pasos para llegar a\(p_1\to p_{k+1}\) desde\(p_1\to p_k\) Esto significa que toma\(2(100−1)\) pasos para llegar a\(p_1\to p_{100}\) (restar\(1\) porque\(p_1\to p_2\) se afirma como premisa). Se necesita un paso final para aplicar el desapego para implicar\(p_{100}\)