5.1: Definiciones básicas y operaciones

Última actualización
Guardar como PDF

Page ID: 117255

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Matriz de Orden e Igualdad

Definición$\PageIndex{1}$: Matrix

Una matriz es una matriz rectangular de elementos de la forma

\ begin {ecuación*} A =\ left (\ begin {array} {ccccc} a_ {11} & a_ {12} & a_ {13} &\ cdots & a_ {1n}\\ a_ {21} & a_ {22} & a_ {23} &\ cdots & a_ {2n}\\ a_ {31} & a_ {32} & a_ _ {33} &\ cdots & a_ {3n}\\\ vdots &\ vdots &\ vdots &\ ddots &\ vdots &\ vdots\\ a_ {m1} & a_ { m2} & a_ {m3} &\ cdots & a_ {mn}\\\ end {array}\ derecha)\ final {ecuación*}

Una manera conveniente de describir una matriz en general es designar cada entrada a través de su posición en la matriz. Es decir, la entrada$a_{34}$ es la entrada en la tercera fila y cuarta columna de la matriz$A\text{.}$ Dependiendo de la situación, decidiremos de antemano a qué conjunto pertenecerán las entradas en una matriz. Por ejemplo, podríamos suponer que cada entrada$a_{ij}$ ($1 \leq i\leq m\text{,}$$1 \leq j \leq n$) es un número real. En ese caso usaríamos$M_{m\times n}(\mathbb{R})$ para representar el conjunto de todas$m$ por$n$ matrices cuyas entradas son números reales. Si decidimos que las entradas en una matriz deben provenir de un conjunto$S\text{,}$ que usamos$M_{m\times n}(S)$ para denotar todas esas matrices.

Definición$\PageIndex{2}$: The Order of a Matrix

Una matriz$A$ que tiene$m$ filas y$n$ columnas se llama matriz$m\times n$ (leída “$m$por$n$”), y se dice que tiene orden$m \times n\text{.}$

Dado que es bastante engorroso escribir la matriz rectangular grande arriba cada vez que deseamos discutir la forma generalizada de una matriz, es una práctica común reemplazar lo anterior por$A = \left(a_{ij}\right)\text{.}$ En general, a las matrices a menudo se les da nombres que son letras mayúsculas y se usa la letra minúscula correspondiente para entradas individuales. Por ejemplo la entrada en la tercera fila, segunda columna de una matriz llamada$C$ sería$c_{32}\text{.}$

Ejemplo$\PageIndex{1}$: Orders of Some Matrices

$A =\left( \begin{array}{cc} 2 & 3 \\ 0 & -5 \\ \end{array} \right)$,$B =\left( \begin{array}{c} 0 \\ \frac{1}{2} \\ 15 \\ \end{array} \right)$, y$D =\left( \begin{array}{ccc} 1 & 2 & 5 \\ 6 & -2 & 3 \\ 4 & 2 & 8 \\ \end{array} \right)$ son$2\times 2\text{,}$$3\times 1\text{,}$ y$3\times 3$ matrices, respectivamente.

Como ahora entendemos cómo es una matriz, estamos en condiciones de investigar las operaciones de álgebra matricial para las que los usuarios han encontrado más aplicaciones.

Primero nos preguntamos: ¿Es la matriz$A =\left( \begin{array}{cc} 1 & 2 \\ 3 & 4 \\ \end{array} \right)$ igual a la matriz$B =\left( \begin{array}{cc} 1 & 2 \\ 3 & 5 \\ \end{array} \right)\text{?}$ No, no lo son porque las entradas correspondientes en la segunda fila, segunda columna de las dos matrices no son iguales.

Siguiente, es$A =\left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{array} \right)$ igual a$B=\left( \begin{array}{cc} 1 & 2 \\ 4 & 5 \\ \end{array} \right)\text{?}$ No, aunque las entradas correspondientes en las dos primeras columnas son idénticas,$B$ no tiene una tercera columna para comparar con la de$A\text{.}$ Formalizamos estas observaciones en la siguiente definición.

Definición$\PageIndex{3}$: Equality of Matrices

Se dice que una matriz$A$ es igual a matriz$B$ (escrita$A = B$) si y solo si:

$A$y$B$ tienen el mismo orden, y
todas las entradas correspondientes son iguales: es decir,$a_{ij}$ =$b_{ij}$ para todas las$i$$j\text{.}$

Adición de Matrices y Multiplicación Escalar

Las dos primeras operaciones que introducimos son muy naturales y probablemente no causen mucha confusión. El primero es la adición de matriz. Parece natural que si$A =\left( \begin{array}{cc} 1 & 0 \\ 2 & -1 \\ \end{array} \right)$ y$B =\left( \begin{array}{cc} 3 & 4 \\ -5 & 2 \\ \end{array} \right)$, entonces

\ begin {ecuación*} A + B =\ left (\ begin {array} {cc} 1+3 & 0+4\\ 2-5 & -1+2\\\ end {array}\ right) =\ left (\ begin {array} {cc} 4 & 4\\ -3 & 1\\\ end {array}\ right). \ end {ecuación*}

No obstante, si$A=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 0 & 1 & 2 \\ \end{array} \right)$ y$B = \left( \begin{array}{cc} 3 & 0 \\ 2 & 8 \\ \end{array} \right)\text{,}$ hay una manera natural de agregarlos para darnos$A+B\text{?}$ No, los órdenes de las dos matrices deben ser idénticos.

Definición$\PageIndex{4}$: Matrix Addition

Dejar$A$ y$B$ ser$m\times n$ matrices. Entonces$A+B$ es una$m\times n$ matriz donde$(A + B)_{ij} = a_{ij} + b_{ij}$ (léase “La entrada$i$ th$j$ th de la matriz$A + B$ se obtiene sumando la$i$ ésima entrada de$A$ a la$j$ ésima entrada de la$i$$j$ ésima entrada de$B$”). Si los órdenes de$A$ y no$B$ son idénticos, no$A+B$ se define.

En definitiva,$A + B$ se define si y sólo si$A$ y$B$ son del mismo orden.

Otra operación de uso frecuente es la de multiplicar una matriz por un número, comúnmente llamado escalar en este contexto. Los escalares normalmente provienen del mismo conjunto que las entradas en una matriz. Por ejemplo, si$A\in M_{m\times n}(\mathbb{R})\text{,}$ un escalar puede ser cualquier número real.

Ejemplo$\PageIndex{2}$: A Scalar Product

Si$c = 3$ y si$A =\left( \begin{array}{cc} 1 & -2 \\ 3 & 5 \\ \end{array} \right)$ y deseamos encontrar$c A\text{,}$ parece natural multiplicar cada entrada de$A$ por 3 para que$3 A =\left( \begin{array}{cc} 3 & -6 \\ 9 & 15 \\ \end{array} \right)\text{,}$ y así es precisamente la forma en que se define la multiplicación escalar.

Definición$\PageIndex{5}$: Scalar Multiplication

Dejar$A$ ser una$m \times n$ matriz y$c$ un escalar. Entonces$c A$ se obtiene la$m\times n$ matriz multiplicando los$c$ tiempos de cada entrada de$A\text{;}$ eso es$(c A)_{ij} = c a_{ij}\text{.}$

Multiplicación de Matriz

Una definición que resulta más incómoda de motivar es el producto de dos matrices. Consulte Ejercicio$\PageIndex{8}$ para intentar hacerlo. Con el tiempo, el lector verá que la siguiente definición del producto de matrices será muy útil, y proporcionará un sistema algebraico que es bastante similar al álgebra elemental.

Aquí hay un video de introducción a la multiplicación matricial.

Definición$\PageIndex{6}$: Matrix Multiplication

Dejar$A$ ser una$m\times n$ matriz y dejar$B$ ser una$n\times p$ matriz. El producto de$A$ y$B\text{,}$ denotado por$AB\text{,}$ es una$m\times p$ matriz cuya entrada de columna$i$$j$ th fila th es

\ begin {equation*}\ begin {split} (A B) _ {ij} &= a_ {i 1} b_ {1 j} +a_ {i 2} b_ {2 j} +\ cdots +a_ {i n} b_ {n j}\\ &=\ sum_ {k=1} ^n a_ {i k} b_ {k}\ end split {}\ end {ecuación*}

para$1\leq i\leq m$ y$1\leq j\leq p\text{.}$

La mecánica de computar una entrada en el producto de dos matrices se ilustra en la Figura$\PageIndex{1}$.

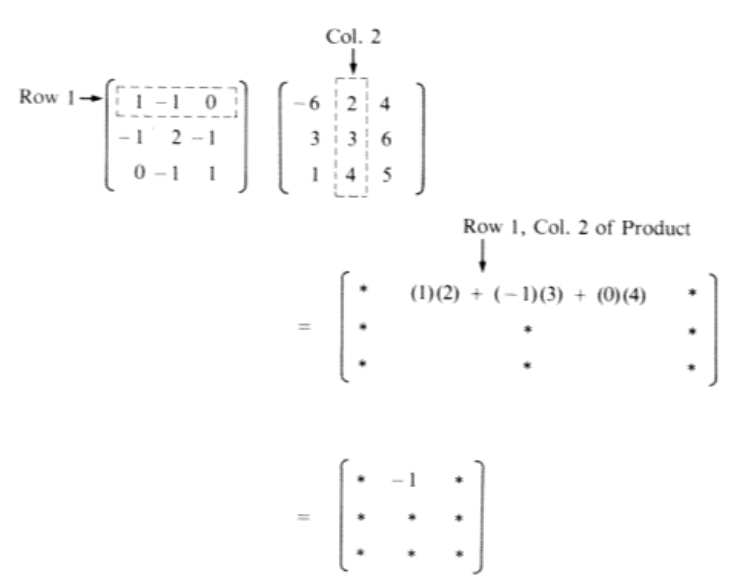$clipboard_e0eabc15276f0ca8dda20936a4eb1cf9a.png$ Figura$\PageIndex{1}$: Cálculo de una entrada en el producto de dos matrices de 3 por 3

El cálculo de un producto puede tomar una cantidad considerable de tiempo en comparación con el tiempo requerido para agregar dos matrices. Supongamos que$A$ y$B$ son$n\times n$ matrices; entonces$(A B)_{ij}$ se determina realizando$n$ multiplicaciones y$n-1$ adiciones. El producto completo toma$n^3$ multiplicaciones y$n^3 - n^2$ adiciones. Esto se compara con$n^2$ las adiciones para la suma de dos$n\times n$ matrices. El producto de dos matrices de 10 por 10 requerirá 1,000 multiplicaciones y 900 adiciones, claramente un trabajo que asignarías a una computadora. La suma de dos matrices requiere de 100 adiciones más modestas. Este análisis se basa en el supuesto de que la multiplicación matricial se realizará utilizando la fórmula que se da en la definición. Existen métodos más avanzados que, en teoría, reducen los recuentos de operaciones. Por ejemplo, el algoritmo de Strassen (https://en.wikipedia.org/wiki/Strassen_algorithm) calcula el producto de dos$n$ por$n$ matrices en$7\cdot 7^{\log _2n}-6\cdot 4^{\log _2n}\approx 7 n^{2.808}$ operaciones. Hay problemas prácticos involucrados en el uso real del algoritmo en muchas situaciones. Por ejemplo, el error de redondeo puede ser más problemático que con la fórmula estándar.

Ejemplo$\PageIndex{3}$: A Matrix Product

Dejar$A =\left( \begin{array}{cc} 1 & 0 \\ 3 & 2 \\ -5 & 1 \\ \end{array} \right)\text{,}$ una$3\times 2$ matriz, y dejar$B =\left( \begin{array}{c} 6 \\ 1 \\ \end{array} \right)\text{,}$ una$2\times 1$ matriz. Entonces$A B$ es una$3 \times 1$ matriz:

\ begin {ecuación*} A B =\ left (\ begin {array} {cc} 1 & 0\\ 3 & 2\\ -5 & 1\\\ end {array}\ end {array}\ right)\ left (\ begin {array} {c} 6\\ 1\\ end {array}\\ right) =\ left (\ begin {array} {c} 1\ cdot 6+0\ cdot 1\ 3\ cdot 6 + 2\ cdot 1\\ -5\ cdot 6 + 1\ cdot 1\\\ end {array}\ derecha) =\ left (\ begin {array} {c} 6\\ 20\ \ -29\\\ end {array}\ derecha)\ end {ecuación*}

Observaciones:

El producto$A B$ se define sólo si$A$ es una$m\times n$ matriz y$B$ es una$n\times p$ matriz; es decir, los dos números “internos” deben ser iguales. Además, el orden de la matriz del producto$A B$ son los números “externos”, en este caso$m\times p\text{.}$
Es aconsejable determinar primero el orden de una matriz de producto. Por ejemplo, si$A$ es una$3\times 2$ matriz y$B$ es una$2\times 2$ matriz, entonces$A B$ es una$3\times 2$ matriz de la forma
\ begin {ecuation*} A B =\ left (\ begin {array} {cc} c_ {11} & c_ {12}\\ c_ {21} & c_ {22}\\ c_ {31} & c_ {32}\\ end {array}\ right)\ end { ecuación*}
Luego para obtener, por ejemplo,$c_{31}\text{,}$ multiplicamos las entradas correspondientes en la tercera fila de$A$ veces la primera columna de$B$ y sumamos los resultados.

Ejemplo$\PageIndex{4}$: Multiplication with a Diagonal Matrix

Dejar$A =\left( \begin{array}{cc} -1 & 0 \\ 0 & 3 \\ \end{array} \right)$ y$B =\left( \begin{array}{cc} 3 & 10 \\ 2 & 1 \\ \end{array} \right)$. Entonces$A B =\left( \begin{array}{cc} -1\cdot 3 + 0\cdot 2 & -1\cdot 10+0\cdot 1 \\ 0\cdot 3+3\cdot 2 & 0\cdot 10+3\cdot 1 \\ \end{array} \right)= \left( \begin{array}{cc} -3 & -10 \\ 6 & 3 \\ \end{array} \right)$

El efecto neto es multiplicar la primera fila de$B$ por$-1$ y la segunda fila de$B$ por 3.

Nota:$B A =\left( \begin{array}{cc} -3 & 30 \\ - 2 & 3 \\ \end{array} \right) \neq A B\text{.}$ Las columnas de$B$ se multiplican por$-1$ y 3 cuando se cambia el orden.

Observaciones:

Una$n\times n$ matriz se llama matriz cuadrada.
Si$A$ es una matriz cuadrada,$A A$ se define y se denota por$A^2$, y$A A A = A^3\text{,}$ etc.
Las $m\times n$matrices cuyas entradas son todas 0 se denotan por$\pmb{0}_{m\times n}\text{,}$ o simplemente$\pmb{ 0}\text{,}$ cuando no surge confusión con respecto al orden.

Ejercicios

Ejercicio$\PageIndex{1}$

Dejar$A=\left( \begin{array}{cc} 1 & -1 \\ 2 & 3 \\ \end{array} \right)\text{,}$$B =\left( \begin{array}{cc} 0 & 1 \\ 3 & -5 \\ \end{array} \right)$, y$C=\left( \begin{array}{ccc} 0 & 1 & -1 \\ 3 & -2 & 2 \\ \end{array} \right)$

Computación$A B$ y$B A\text{.}$
Computación$A + B$ y$B + A\text{.}$
Si$c = 3\text{,}$ mostrar que$c(A + B) = c A + c B\text{.}$
Demostrar que$(A B)C = A(B C)\text{.}$
Compute$A^2 C\text{.}$
Compute$B + \pmb{0}\text{.}$
Calcular$A \pmb{0}_{2\times 2}$ y$\pmb{0}_{2\times 2} A\text{,}$ dónde$\pmb{0}_{2\times 2}$ está la matriz$2\times 2$ cero.
Calcular$0A\text{,}$ donde 0 es el número real (escalar) cero.
Deja$c = 2$ y$d = 3\text{.}$ muestra eso$(c + d)A = c A + d A\text{.}$

Contestar

Para las partes c, d e i de este ejercicio, sólo se necesita una verificación. Aquí, suministramos el resultado que aparecerá en ambos lados de la igualdad.

$\displaystyle AB=\left( \begin{array}{cc} -3 &6 \\ 9 & -13 \\ \end{array} \right) \quad BA=\left( \begin{array}{cc} 2 & 3 \\ -7 & -18 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cc} 1 & 0 \\ 5 & -2 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cc} 3 & 0 \\ 15 & -6 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{ccc} 18 & -15 & 15 \\ -39 & 35 & -35 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{ccc} -12 & 7 & -7 \\ 21 & -6 & 6 \\ \end{array} \right)$
$\displaystyle B+0=B$
$\displaystyle \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cc} 5 & -5 \\ 10 & 15 \\ \end{array} \right)$

Ejercicio$\PageIndex{2}$

Dejar$A = \left( \begin{array}{ccc} 1 & 0 & 2 \\ 2 & -1 & 5 \\ 3 & 2 & 1 \\ \end{array} \right)$,$B =\left( \begin{array}{ccc} 0 & 2 & 3 \\ 1 & 1 & 2 \\ -1 & 3 & -2 \\ \end{array} \right)$, y$C=\left( \begin{array}{cccc} 2 & 1 & 2 & 3 \\ 4 & 0 & 1 & 1 \\ 3 & -1 & 4 & 1 \\ \end{array} \right)$ Calcular, si es posible;

$\displaystyle A - B$
$\displaystyle A B$
$\displaystyle A C - B C$
$\displaystyle A(B C)$
$\displaystyle C A - C B$
$\displaystyle C \left( \begin{array}{c} x \\ y \\ z \\ w \\ \end{array} \right)$

Ejercicio$\PageIndex{3}$

Vamos$A =\left( \begin{array}{cc} 2 & 0 \\ 0 & 3 \\ \end{array} \right)$. Encuentra una matriz$B$ tal que$A B = I$ y$B A = I\text{,}$ dónde$I = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right)\text{.}$

Contestar: $\left( \begin{array}{cc} 1/2 & 0 \\ 0 & 1/3 \\ \end{array} \right)$

Ejercicio$\PageIndex{4}$

Encuentra$A I$ y$B I$ dónde$I$ está como en Ejercicio$\PageIndex{3}$, dónde$A = \left( \begin{array}{cc} 1 & 8 \\ 9 & 5 \\ \end{array} \right)$ y$B = \left( \begin{array}{cc} -2 & 3 \\ 5 & -7 \\ \end{array} \right)\text{.}$ ¿Qué notas?

Ejercicio$\PageIndex{5}$

Averiguar$A^3$ si$A=\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{array} \right)$. ¿A qué es$A^{15}$ igual?

Contestar: $A^3=\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 8 & 0 \\ 0 & 0 & 27 \\ \end{array} \right)$$A^{15}=\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 32768 & 0 \\ 0 & 0 & 14348907 \\ \end{array} \right)$

Ejercicio$\PageIndex{6}$

Determinar$I^2$ y$I^3 \text{ if }$$I = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right)\text{.}$
Lo que es$I^n$ igual para cualquier$n\geq 1\text{?}$
Demuestra tu respuesta a la parte (b) por inducción.

Ejercicio$\PageIndex{7}$

Si
\ begin {ecuación*} A =\ left (\ begin {array} {cc} 2 & 1\\ 1 & -1\\\ end {array}\ right), X =\ left (\ begin {array} {c} x_1\\ x_2\\ end {array}\\ right)\ textrm {, y} B =\ left (\ begin {array} {c} 3\ 1\\\ end {array}\ right),\ end {equation*}
mostrar que$A X =B$ es una manera de expresar el sistema$\begin{array}{c}2x_1 + x_2 = 3\\ x_1 - x_2= 1\\ \end{array}$ usando matrices.
Expresar los siguientes sistemas de ecuaciones usando matrices:
1. $\displaystyle \begin{array}{c} 2 x_1- x_2= 4\\ x_1+ x_2= 0\\ \end{array}$
2. $\displaystyle \begin{array}{c} x_1+ x_2+ 2 x_3= 1\\ x_1+ 2 x_2-x_3= -1\\ x_1+ 3 x_2+x_3= 5\\ \end{array}$
3. $\displaystyle \begin{array}{c} x_1+x_2\quad\quad= 3\\ \quad \quad x_2\quad\quad= 5\\ x_1 \quad \quad+ 3x_3= 6\\ \end{array} $

Contestar

$Ax=\left( \begin{array}{c} 2x_1+1x_2 \\ 1x_1-1x_2 \\ \end{array} \right)$ equals $\left( \begin{array}{c} 3 \\ 1 \\ \end{array} \right)$ if and only if both of the equalities $2x_1+x_2=3 \textrm{ and } x_1-x_2=1$ are true.
(i)$A=\left( \begin{array}{cc} 2 & -1 \\ 1 & 1 \\ \end{array} \right)$$x=\left( \begin{array}{c} x_1 \\ x_2 \\ \end{array} \right)$$B=\left( \begin{array}{c} 4 \\ 0 \\ \end{array} \right)$
$A=\left( \begin{array}{ccc} 1 & 1 & 2 \\ 1 & 2 & -1 \\ 1 & 3 & 1 \\ \end{array} \right)$$x=\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)$$B=\left( \begin{array}{c} 1 \\ -1 \\ 5 \\ \end{array} \right)$
$A=\left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 3 \\ \end{array} \right)$$x=\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)$$B=\left( \begin{array}{c} 3 \\ 5 \\ 6 \\ \end{array} \right)$

Ejercicio$\PageIndex{8}$

En este ejercicio, proponemos mostrar cómo la multiplicación matricial es una operación natural. Supongamos que una panadería produce pan, pasteles y pasteles todos los días de la semana, de lunes a viernes. Con base en el historial de ventas pasado, la panadería produce diversos números de cada producto cada día, resumidos en la$5 \times 3$ matriz$D\text{.}$ Cabe señalar que el pedido podría describirse como “número de días por número de productos”. Por ejemplo, el miércoles (tercer día) el número de pasteles (segundo producto en nuestra lista) que se producen es$d_{3,2} = 4\text{.}$

\ begin {ecuación*} D =\ left (\ begin {array} {ccc} 25 & 5 & 5\\ 14 & 5 & 8\\ 20 & 4 & 15\\ 18 & 5 & 7\\ 35 & 10 & 9\\ end {array}\\ derecha)\ end {ecuación*}

Los ingredientes principales de estos productos son la harina, el azúcar y los huevos. Asumimos que otros ingredientes siempre están en un amplio suministro, pero necesitamos estar seguros de tener los tres principales disponibles. Para cada uno de los tres productos, La cantidad de cada ingrediente que se necesita se resume en la matriz$3 \times 3\text{,}$ o “número de productos por número de ingredientes” Por ejemplo,$P\text{.}$ para hornear un pastel (segundo producto) necesitamos$P_{2,1}=1.5$ tazas de harina (primer ingrediente). En cuanto a las unidades: la harina y el azúcar se dan en tazas por unidad de cada producto, mientras que los huevos se dan en huevos individuales por unidad de cada producto.

\ begin {ecuación*} P =\ left (\ begin {array} {ccc} 2 & 0.5 & 0\\ 1.5 & 1 & 2\\ 1 & 1 & 1 & 1\\\ end {array}\ derecha)\ end {ecuación*}

Estas cantidades están “maquilladas”, ¡así que no las uses para hacer tu propio horneado!

¿Cuántas tazas de harina necesitará la panadería todos los lunes? Presta mucha atención a cómo computas tu respuesta y las unidades de cada número.
¿Cuántos huevos necesitará la panadería todos los miércoles?
Calcular el producto matriz ¿$D P\text{.}$Qué notas?
Supongamos que los costos de los ingredientes son$\$0.12$ para una taza de harina,$\$0.15$ por una taza de azúcar y$\$0.19$ por un huevo. ¿Cómo se puede poner esta información en una matriz que pueda multiplicarse de manera significativa por una de las otras matrices en este problema?