6.1: Definiciones básicas

En el Capítulo 1 introdujimos el concepto del producto cartesiano de conjuntos. Supongamos que una persona posee tres camisas y dos pares de pantalones. Más precisamente, let\(A = \{\textrm{blue shirt}, \textrm{tan shirt}, \textrm{mint green shirt}\}\) y\(B = \{\textrm{grey slacks}, \textrm{tan slacks}\}\text{.}\) Entonces\(A\times B\) es el conjunto de las seis combinaciones posibles de camisas y pantalones que el individuo podría usar. Sin embargo, un individuo puede desear restringirse a sí mismo a combinaciones que estén coordinadas por colores o “relacionadas”. Esto puede no ser todos los pares posibles en\(A\times B\) pero ciertamente será un subconjunto de\(A\times B\text{.}\) Por ejemplo, uno de esos subconjunto puede ser

\ begin {ecuación*}\ {(\ textrm {camisa azul},\ textrm {pantalones grises}), (\ textrm {camisa azul},\ textrm {pantalones bronceados}), (\ textrm {camisa verde menta},\ textrm {pantalones bronceados})\}. \ end {ecuación*}

Relaciones entre dos conjuntos

Definición\(\PageIndex{1}\): Relation

Dejar\(A\) y\(B\) ser conjuntos. Una relación de\(A\) hacia\(B\) es cualquier subconjunto de\(A\times B\text{.}\)

Ejemplo\(\PageIndex{1}\): A Simple Example

Dejar\(A = \{1, 2, 3\}\) y\(B = \{4, 5\}\text{.}\) Entonces\(\{(1, 4), (2, 4), (3, 5)\}\) es una relación\(B\text{.}\) de\(A\) hacia Por supuesto, hay muchos otros que podríamos describir; 64, para ser exactos.

Ejemplo\(\PageIndex{2}\): Divisibility Example

Dejar\(A = \{2, 3, 5, 6\}\) y definir una relación\(r\) de\(A\) hacia\(A\) por\((a, b) \in r\) si y solo si se\(a\) divide equitativamente en\(b\text{.}\) El conjunto de parejas que califican para la membresía es\(r = \{(2, 2), (3, 3), (5, 5), (6, 6), (2, 6), (3, 6)\}\text{.}\)

Relaciones en un Set

Definición\(\PageIndex{2}\): Relation on a Set

Una relación de un conjunto\(A\) en sí mismo se llama relación sobre\(A\text{.}\)

La relación “divide” en Ejemplo\(\PageIndex{2}\) aparecerá a lo largo del libro. Aquí hay una definición general sobre todo el conjunto de enteros.

Definición \(\PageIndex{3}\): Divides

\(a, b \in \mathbb{Z}\text{,}\)\(a \neq 0\text{.}\)Digamos que\(a\) divide\(b\text{,}\) denotado\(a \mid b\text{,}\) si y solo si existe un entero\(k\) tal que\(a k = b\text{.}\)

Tenga mucho cuidado al escribir sobre la relación “divide”. El símbolo de línea vertical utilizado para esta relación, si se escribe descuidadamente, puede parecer división. Si bien\(a \mid b\) es verdadero o falso,\(a/b\) es un número.

Con base en la ecuación\(a k = b\text{,}\) podemos decir que\(a|b\) es equivalente\(k= \frac{b}{a}\text{,}\) o se\(a\) divide uniformemente\(b\text{.}\) en De hecho el “divide” es la abreviatura de “divide uniformemente en”. Podría encontrar la ecuación\(k= \frac{b}{a}\) inicialmente más fácil de entender, pero a la larga encontraremos la ecuación\(a k = b\) más conveniente.

A veces resulta útil ilustrar una relación con una gráfica. Considera Ejemplo\(\PageIndex{1}\). Se\(r\) puede dibujar una gráfica de como en la Figura\(\PageIndex{1}\). Las flechas indican que 1 está relacionado con 4 bajo\(r\text{.}\) También, 2 está relacionado con 4 bajo\(r\text{,}\) y 3 está relacionado con 5, mientras que la flecha superior denota que\(r\) es una relación de todo el conjunto\(A\) en el conjunto\(B\text{.}\)

Figura\(\PageIndex{1}\): La gráfica de una relación

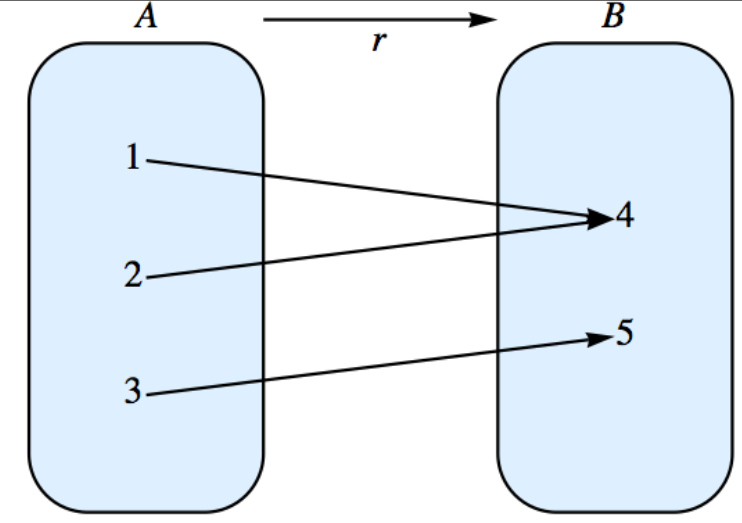
Un elemento típico en una relación\(r\) es un par ordenado.\((x, y)\text{.}\) En algunos casos, se\(r\) puede describir enumerando realmente los pares en los que se encuentran\(r\text{,}\) como en los ejemplos anteriores. Esto puede no ser conveniente si\(r\) es relativamente grande. Otras notaciones se utilizan con ciertas relaciones bien conocidas. Considera la relación “menor que o igual” sobre los números reales. Podríamos definirlo como un conjunto de pares ordenados de esta manera:

\ comenzar {ecuación*}\ le =\ {(x, y) | x\ leq y\}\ fin {ecuación*}

Sin embargo, la notación\(x \leq y\) es clara y autoexplicativa; es una notación más natural, y por lo tanto preferida, para usar que\((x, y) \in \le\text{.}\)

Muchas de las relaciones con las que trabajaremos “se asemejan” a la relación\(\leq\text{,}\) por lo que\(x s y\) es una forma común de expresar el hecho con que\(x\) se relaciona a\(y\) través de la relación\(s\text{.}\)

Notación de relación Dejar\(s\) ser una relación de un conjunto\(A\) a un conjunto\(B\text{.}\) Entonces el hecho de que\((x, y) \in s\) se escribe frecuentemente\(x s y\text{.}\)

Composición de las relaciones

Con\(A = \{2, 3, 5, 8\}\text{,}\)\(B = \{4, 6, 16\}\text{,}\) y\(C = \{1, 4, 5, 7\}\text{,}\) dejar\(r\) ser la relación “divide”, de\(A\) dentro\(B\text{,}\) y dejar que\(s\) sea la relación\(\leq\) de\(B\) en\(C\text{.}\) So\(r = \{(2, 4), (2, 6), (2,16), (3, 6), (8, 16)\}\) y\(s = \{(4, 4), (4, 5), (4, 7), (6, 7)\}\text{.}\)

Observe que en Figura\(\PageIndex{2}\) que podemos, para ciertos elementos de\(A\text{,}\) pasar por elementos en\(B\) a resultados en\(C\text{.}\) Eso es:

Mesa\(\PageIndex{1}\)

\(2 | 4 \textrm{ and } 4 \leq 4\)

\(2 | 4 \textrm{ and } 4 \leq 5\)

\(2 | 4 \textrm{ and } 4 \leq 7\)

\(2| 6 \textrm{ and } 6 \leq 7\)

\(3| 6 \textrm{ and } 6 \leq 7\)

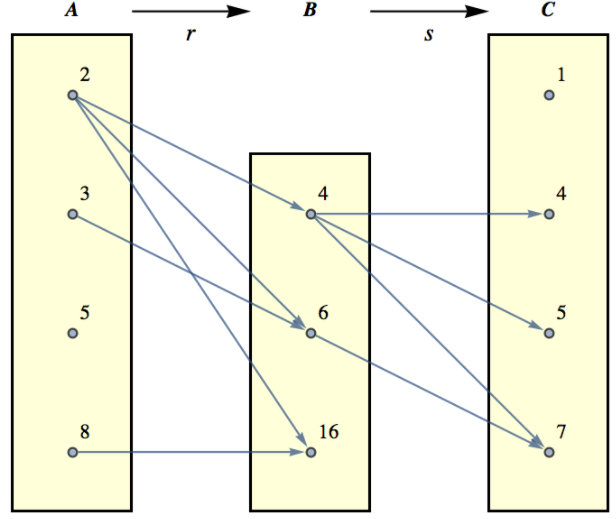Figura\(\PageIndex{2}\): Composición de la relación - una vista gráfica

Con base en esta observación, podemos definir una nueva relación, llamarla\(rs\text{,}\) de\(A\) hacia\(C\text{.}\)\((a, c)\) Para estar en\(rs\text{,}\) ella debe ser posible recorrer un camino en Figura\(\PageIndex{2}\) de\(a\) a\(c\text{.}\) En otras palabras,\((a, c) \in rs\) si y solo si\((\exists b)_B(a r b \textrm{ and } b s c)\text{.}\) El nombre\(rs\) fue elegido porque nos recuerda que esta nueva relación la formaron las dos relaciones anteriores\(r\) y\(s\text{.}\) El listado completo de todos los elementos en\(rs\) es\(\{(2, 4), (2, 5), (2, 7), (3, 7)\}\text{.}\) Resumimos en una definición.

Definición \(\PageIndex{4}\): Composition of Relations

Dejar\(r\) ser una relación de un conjunto\(A\) a un conjunto\(B\text{,}\) y dejar\(s\) ser una relación de\(B\) a un conjunto\(C\text{.}\) La composición de\(r\) con\(s\text{,}\) escrito\(rs\text{,}\) es el conjunto de pares de la forma\((a, c) \in A\times C\text{,}\) donde\((a, c) \in rs\) si y solo si existe \(b \in B\)tal que\((a, b) \in r\) y\((b, c) \in s\text{.}\)

Observación: Una advertencia a aquellos lectores familiarizados con la composición de funciones. (Para los que no lo son, desatiendan esta observación. Se repetirá en un lugar apropiado en el próximo capítulo.) Como se indicó anteriormente, la forma tradicional de describir una composición de dos relaciones es\(rs\) donde\(r\) está la primera relación y\(s\) la segunda. Sin embargo, la composición de la función se expresa tradicionalmente en el orden opuesto:\(s\circ r\text{,}\) donde\(r\) está la primera función y\(s\) es la segunda.

Ejercicios

Ejercicio\(\PageIndex{1}\)

Para cada una de las siguientes relaciones\(r\) definidas en\(\mathbb{P}\text{,}\) determinar cuál de los pares ordenados dados pertenecen a\(r\)

1. \(x r y\)iff\(x|y\text{;}\) (2, 3), (2, 4), (2, 8), (2, 17)
2. \(x r y\)iff\(x \leq y\text{;}\) (2, 3), (3, 2), (2, 4), (5, 8)
3. \(x r y\)iff\(y =x^2\); (1,1), (2, 3), (2, 4), (2, 6)

Contestar

1. \(\displaystyle (2,4), (2,8)\)
2. \(\displaystyle (2, 3), (2, 4), (5,8)\)
3. \(\displaystyle (1,1), (2,4)\)

Ejercicio\(\PageIndex{2}\)

Las siguientes relaciones están en\(\{1, 3, 5\}\text{.}\) Let\(r\) be the relation\(x r y\) iff\(y = x + 2\) and\(s\) the relation\(x s y\) iff\(x \leq y\text{.}\)

1. Listar todos los elementos en\(rs\text{.}\)
2. Listar todos los elementos en\(sr\text{.}\)
3. Ilustrar\(rs\) y\(sr\) a través de un diagrama.
4. ¿La relación es\(rs\) igual a la relación\(sr\text{?}\)

Ejercicio\(\PageIndex{3}\)

Dejar\(A = \{1,2,3,4,5\}\) y definir\(r\)\(A\) por\(x r y\) iff\(x + 1 = y\text{.}\) Definimos\(r^2 = r r\) y\(r^3 = r^2 r\text{.}\) Find:

1. \(\displaystyle r\)
2. \(\displaystyle r^2\)
3. \(\displaystyle r^3\)

Contestar

1. \(\displaystyle r=\{(1,2), (2,3), (3,4), (4,5)\}\)
2. \(\displaystyle r^2 = \{(1,3), (2,4), (3,5)\}=\{(x,y) : y=x+2, x,y\in A\}\)
3. \(\displaystyle r^3=\{(1,4), (2,5)\}=\{(x,y) : y=x+3, x,y \in A\}\)

Ejercicio\(\PageIndex{4}\)

Dado\(s\) y\(t\text{,}\) relaciones sobre\(\mathbb{Z}\text{,}\)\(s = \{(1, n) : n \in \mathbb{Z}\}\) y\(t= \{(n, 1) : n \in \mathbb{Z}\}\text{,}\) qué son\(st\) y\(ts\text{?}\) Pista: Incluso cuando una relación involucra conjuntos infinitos, a menudo se puede obtener información sobre ellos dibujando gráficos parciales.

Ejercicio \(\PageIndex{5}\)

\(\rho\)Sea la relación sobre el conjunto de poder,\(\mathcal{P}(S )\text{,}\) de un conjunto finito\(S\) de cardinalidad\(n\) definido\(\rho\) por\((A,B) \in \rho\) iff\(A\cap B = \emptyset\text{.}\)

1. Considerar el caso específico\(n = 3\text{,}\) y determinar la cardinalidad del conjunto\(\rho\text{.}\)
2. Cuál es la cardinalidad de\(\rho\) para una arbitraria\(n\text{?}\) Expresa tu respuesta en términos de\(n\text{.}\) (Pista: Hay tres lugares a los que cada elemento de S puede ir en la construcción de un elemento de\(\rho\text{.}\))

Contestar

1. Cuando\(n=3\text{,}\) hay 27 pares en la relación.
2. Imagínese construir un par de subconjuntos disjuntos de\(S\text{.}\) Para cada elemento de\(S\) hay tres lugares a los que puede ir: en el primer conjunto del par ordenado, en el segundo conjunto, o en ninguno de los conjuntos. Por lo tanto, el número de pares en la relación es\(3^n\text{,}\) por la regla del producto.

Ejercicio\(\PageIndex{6}\)

Considera las dos relaciones sobre las personas:\(M\text{,}\) dónde está\(a\) la madre de\(aMb\) si\(b\text{;}\) y\(S\text{,}\) dónde\(aSb\) si\(a\) y\(b\) son hermanos. Describir, en palabras, las dos relaciones\(MS\) y\(SM\) en términos simples en inglés.

Ejercicio\(\PageIndex{7}\)

Dejar\(r_1\text{,}\)\(r_2\text{,}\) y\(r_3\) ser relaciones en cualquier set\(A\text{.}\) Demostrar que si\(r_1\subseteq r_2\) entonces\(r_1r_3\subseteq r_2r_3\text{.}\)

Contestar

Asumir\((x,y)∈r_1r_3\). Esto implica que existen\(z∈A\) tal que\((x,z)∈r_1\) y\((z,y)∈r_3\). Se nos da eso,\(r_1⊆r_2\), lo que implica eso\((x,z)∈r_2\). Combinar esto con\((z,y)∈r_3\) implica eso\((x,y)∈r_2r_3\), lo que lo demuestra\(r_1r_3⊆r_2r_3\).