6.2: Gráficas de relaciones en un conjunto

Última actualización
Guardar como PDF

Page ID: 117264

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección introducimos las gráficas dirigidas como una forma de visualizar las relaciones en un conjunto.

Dígrafos

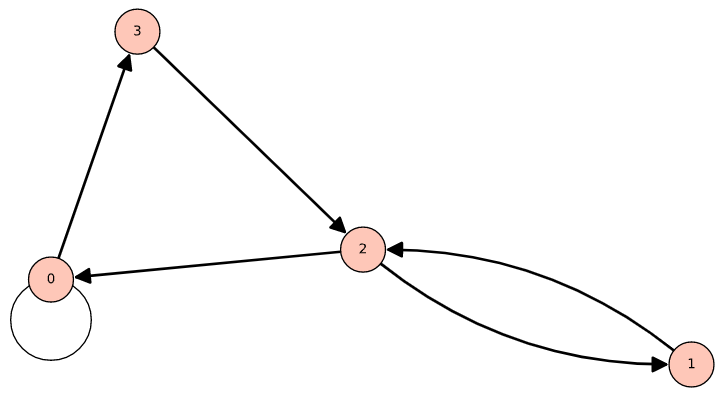
Dejar$A = \{0, 1,2,3\}\text{,}$ y dejar

\ begin {ecuación*} r =\ {(0, 0), (0, 3), (1, 2), (2, 1), (3, 2), (2, 0)\}\ end {ecuación*}

Al representar esta relación como una gráfica, los elementos de$A$ se denominan los vértices de la gráfica. Por lo general, están representados por puntos etiquetados o pequeños círculos. Conectamos vértice$a$ a vértice$b$ con una flecha, llamada borde, yendo de vértice$a$ a vértice$b$ si y solo si$a r b\text{.}$ Este tipo de gráfico de una relación$r$ se llama grafo o dígrafo dirigido . La figura$\PageIndex{1}$ es un dígrafo para$r\text{.}$ Notice que dado que 0 está relacionado consigo mismo, dibujamos un “auto-bucle” en 0.

La ubicación real de los vértices en un dígrafo es inmaterial. La ubicación real de los vértices que elegimos se llama incrustación de una gráfica. La idea principal es colocar los vértices de tal manera que la gráfica sea fácil de leer. Después de dibujar una gráfica de borrador de una relación, podemos decidir reubicar los vértices para que el resultado final sea más limpio. La figura también$\PageIndex{1}$ podría presentarse como en la Figura$\PageIndex{2}$.

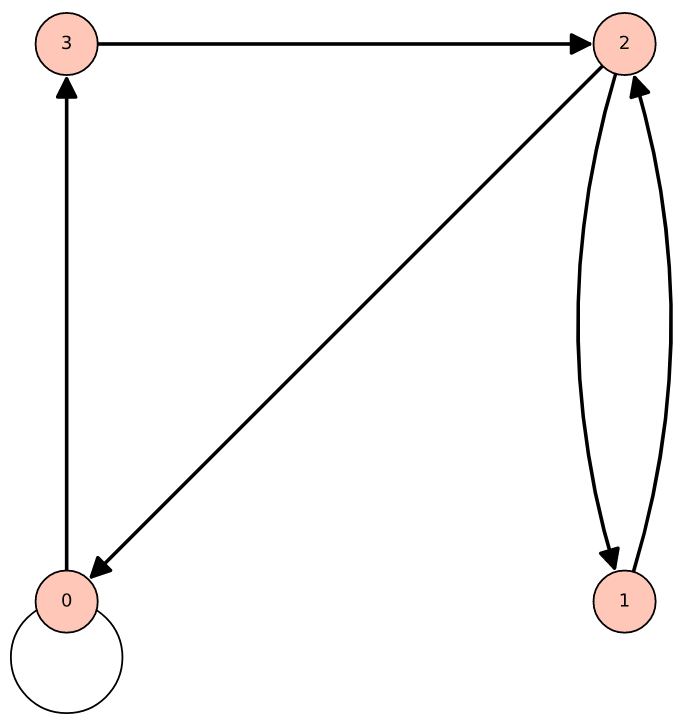
Un vértice de una gráfica también se denomina nodo, punto o cruce. Un borde de una gráfica también se conoce como un arco, una línea o una rama. No se preocupe si dos gráficas de una relación dada se ven diferentes siempre y cuando las conexiones entre vértices sean las mismas en las dos gráficas.

Ejemplo$\PageIndex{1}$: Another Directed Graph

Considera la relación$s$ cuya dígrafa es Figura$\PageIndex{3}$. ¿Qué información nos da esto? El gráfico nos dice que$s$ es una relación sobre$A = \{1, 2, 3\}$ y que$s = \{(1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 3)\}\text{.}$

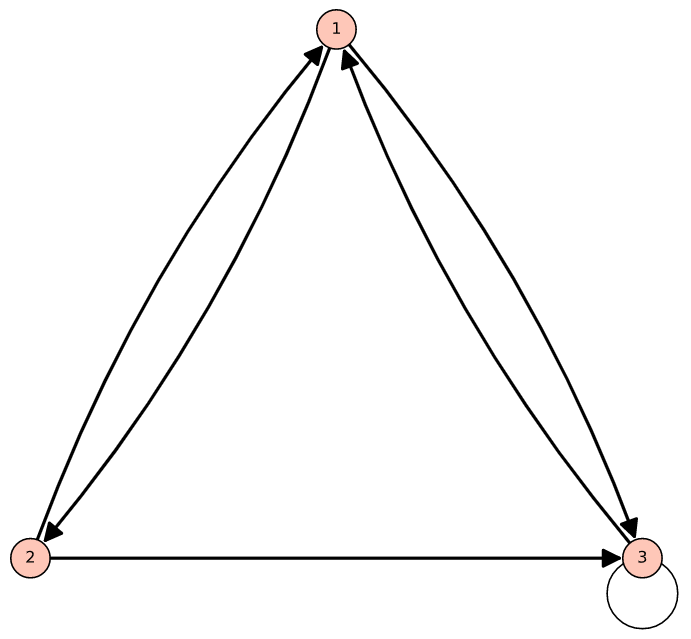
Estaremos construyendo sobre el siguiente ejemplo en la siguiente sección.

Ejemplo$\PageIndex{2}$: Ordering Subsets of a Two Element Universe

Let$B = \{1,2\}\text{,}$ and let$A = \mathcal{P}(B) = \{\emptyset, \{1\}, \{2\}, \{1,2\}\}\text{.}$ Entonces$\subseteq$ es una relación sobre$A$ cuya dígrafa es Figura$\PageIndex{4}$.

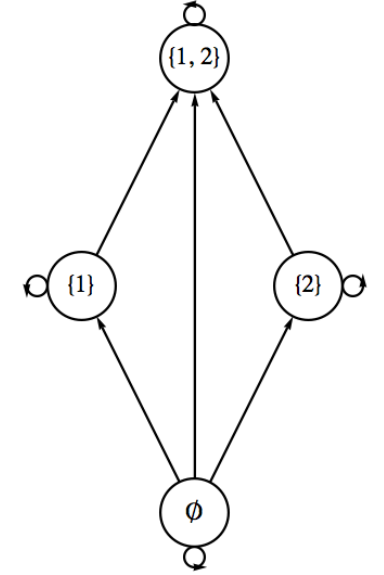$clipboard_e0427f4b66176bc81b0300cf2af0bc2af.png$ Figura $\PageIndex{4}$: Gráfica para la contención de conjuntos en subconjuntos de$\{1,2\}$

Veremos en la siguiente sección que desde entonces$\subseteq$ tiene ciertas propiedades estructurales que describen “ordenamientos parciales”. Podremos dibujar una gráfica tipográfica mucho más simple que esta, pero por ahora la gráfica anterior sirve a nuestros propósitos.

Ejercicios

Ejercicio$\PageIndex{1}$

Dejar$A = \{1, 2, 3, 4\}\text{,}$ y dejar$r$ ser la relación$\leq$ en$A\text{.}$ Dibujar un dígrafo para$r\text{.}$

Contestar

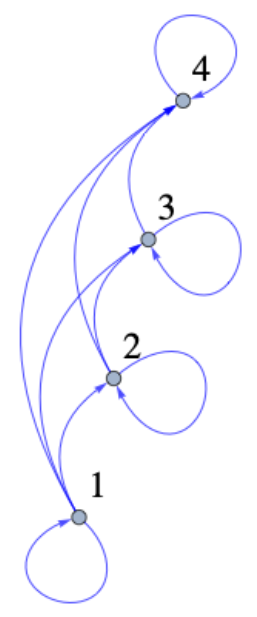
$clipboard_ea09140ac71453cfb0834d7d54648dfe6.png$

Figura$\PageIndex{5}$: Dígrafo para$\leq$

$clipboard_e8ce2c5ec7978bdcc65babe2b61288e7f.png$

Figura$\PageIndex{6}$: Diagrama de Hasse para$\leq$

Ejercicio$\PageIndex{2}$

Dejar$B = \{1,2, 3, 4, 6, 8, 12, 24\}\text{,}$ y dejar$s$ ser la relación “divide” en$B\text{.}$ Dibujar un dígrafo para$s\text{.}$

Ejercicio$\PageIndex{3}$

$t$Vamos$A=\{1,2,3,4,5\}\text{.}$ Definir$A$ por$a t b$ si y solo si$b - a$ es par. Dibuja un dígrafo para$t\text{.}$

Contestar

Ver Figura$\PageIndex{7}$

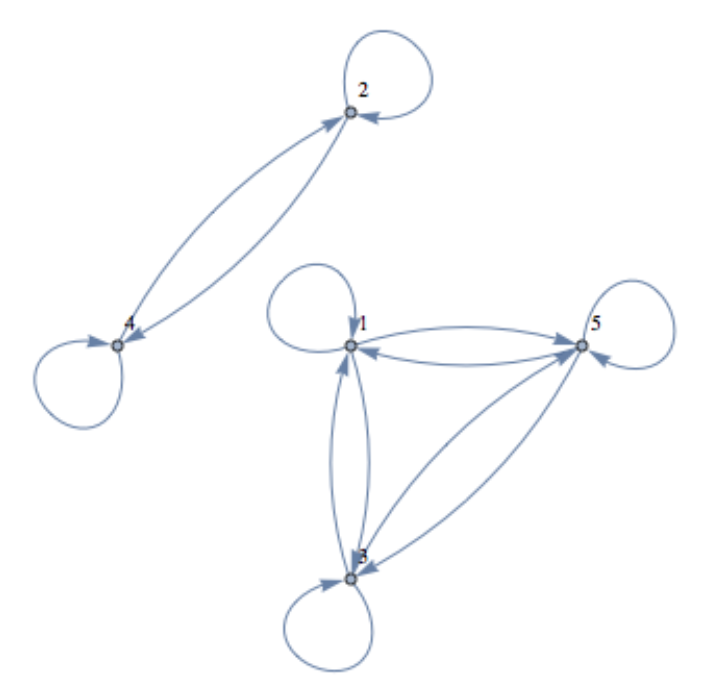
$clipboard_eb94767f831aa7d090c52d93542450a20.png$

Figura$\PageIndex{7}$: Dígrafo de la relación$t$

Ejercicio$\PageIndex{4}$

Dejar$A$ ser el conjunto de cadenas de 0's y 1's de longitud 3 o menos. Esto incluye la cadena vacía,$\lambda\text{,}$ que es la única cadena de longitud cero.

Definir la relación de$d$ on$A$ por$x d y$ si$x$ está contenido dentro$y\text{.}$ Por ejemplo,$01 d 101\text{.}$ Dibuja un dígrafo para esta relación.
Haz lo mismo para la relación$p$ definida por$x p y$ if$x$ es un prefijo de$y\text{.}$ Por ejemplo,$10 p 101\text{,}$ pero$01 p 101$ es false.

Ejercicio$\PageIndex{5}$

Recordemos la relación en el Ejercicio 6.1.5 de la Sección 6.1,$\rho$ definida sobre el conjunto de potencia,$\mathcal{P}(S)\text{,}$ de un conjunto$S\text{.}$ La definición era$(A,B) \in \rho$ iff$A\cap B = \emptyset\text{.}$ Dibujar el dígrafo para$\rho$ donde$S = \{a, b\}\text{.}$

Ejercicio$\PageIndex{6}$

Dejar$C= \{1,2, 3, 4, 6, 8, 12, 24\}$ y definir$t$$C$ por$a t b$ si y sólo si$a$ y$b$ compartir un divisor común mayor que 1. Dibuja un dígrafo para$t\text{.}$