6.3: Propiedades de las Relaciones

Última actualización
Guardar como PDF

Page ID: 117270

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Propiedades Individuales

Consideremos el conjunto$B = \{1, 2, 3, 4, 6, 12, 36, 48\}$ y las relaciones “divide” y$\leq $ en$B\text{.}$ Notamos que estas dos relaciones on$B$ tienen tres propiedades en común:

Cada elemento en se$B$ divide a sí mismo y es menor o igual a sí mismo. A esto se le llama la propiedad reflexiva.
Si buscamos dos elementos de$B$ donde el primero divide al segundo y el segundo divide al primero, entonces nos vemos obligados a elegir los dos números para que sean iguales. Es decir, no hay dos números diferentes relacionados en ambas direcciones. El lector puede verificar que un hecho similar es cierto para la relación$\leq $ en$B\text{.}$ Esto se llama la propiedad antisimétrica.
Siguiente si elegimos tres valores (no necesariamente distintos) de$B$ tales que el primero divide al segundo y el segundo divide al tercero, entonces siempre encontramos que el primer número divide al tercero. Nuevamente, lo mismo es cierto si reemplazamos “divide” por “es menor o igual a”. A esto se le llama la propiedad transitiva.

Las relaciones que satisfacen estas propiedades son de especial interés para nosotros. Las definiciones formales de las propiedades siguen.

Definición$\PageIndex{1}$: Reflexive Relation

Dejar$A$ ser un conjunto y dejar$r$ ser una relación en$A\text{.}$ Entonces$r$ es reflexivo si y solo si$a r a$ para todos$a \in A\text{.}$

Definición$\PageIndex{2}$: Antisymmetric Relation

Dejar$A$ ser un conjunto y dejar$r$ ser una relación en$A\text{.}$ Entonces$r$ es antisimétrico si y sólo si siempre$a r b$ y$a \neq b$ entonces$b r a$ es falso.

Una condición equivalente para la antisimetría es que si$a r b$ y$b r a$ luego$a = b\text{.}$ Te animan a convencerte de que esto es cierto. Esta condición suele ser más conveniente de probar que la definición, aunque probablemente la definición sea más fácil de entender.

Una advertencia sobre la antisimetría: A los estudiantes les resulta difícil entender esta definición con frecuencia. Tenga en cuenta que este término se define a través de una declaración “Si... entonces...”. La pregunta que debes hacer es: ¿Es cierto que cada vez que hay elementos$a$ y$b$ de$A$ dónde$a r b$ y se$a \neq b\text{,}$ deduce que no$b$ está relacionado con$a\text{?}$ Si es así, entonces la relación es antisimétrica?

Otra forma de determinar si una relación es antisimétrica es examinar (o imaginar) su dígrafo. La relación no es antisimétrica si existe un par de vértices que están conectados por aristas en ambas direcciones.

Definición $\PageIndex{3}$: Transitive Relation

Dejar$A$ ser un conjunto y dejar$r$ ser una relación on$A\text{.}$$r$ es transitivo si y solo si cuando$a r b$ y$b r c$ luego$a r c\text{.}$

Pedidos Parciales

No todas las relaciones tienen las tres propiedades discutidas anteriormente, pero las que sí son un tipo especial de relación.

Definición$\PageIndex{4}$: Partial Ordering

Una relación en un conjunto$A$ que es reflexiva, antisimétrica y transitiva se llama orden parcial en$A\text{.}$ Un conjunto en el que hay una relación de orden parcial definida se llama conjunto parcialmente ordenado o poset.

Ejemplo$\PageIndex{1}$: Set Containment as a Partial Ordering

$A$Déjese ser un conjunto. Entonces$\mathcal{P}(A)$ junto con la relación$\subseteq$ (conjunto de contención) es un poset. Para demostrarlo observamos que las tres propiedades se mantienen, como se discute en el Capítulo 4.

Dejar$B \in \mathcal{P}(A)\text{.}$ El hecho que se$B \subseteq B$ desprende de la definición de subconjunto. De ahí que la contención del conjunto sea reflexiva.
Dejemos$B_1, B_2 \in \mathcal{P}(A)$ y asumamos que$B_1\subseteq B_2$ y$B_1\neq B_2$. ¿Podría ser que el$B_2\subseteq B_1\text{?}$ No. Debe haber algún elemento$a\in A$ tal que$a \notin B_1\text{,}$ pero$a\in B_2\text{.}$ Esto es exactamente lo que necesitamos para concluir que no$B_2$ está contenido en$B_1\text{.}$ De ahí que la contención de conjuntos sea antisimétrica.
Dejemos$B_1, B_2,B_3 \in \mathcal{P}(A)$ y asumamos que$B_1 \subseteq B_2$ y$B_2 \subseteq B_3$. ¿Sigue eso$B_1 \subseteq B_3$? Sí, si$a\in B_1\text{,}$ entonces$a\in B_2$ porque$B_1 \subseteq B_2\text{.}$ Ahora que tenemos$a\in B_2$ y hemos asumido$B_2 \subseteq B_3\text{,}$ concluimos que$a\in B_3\text{.}$ Por lo tanto,$B_1\subseteq B_3$ y así establecer la contención es transitiva.

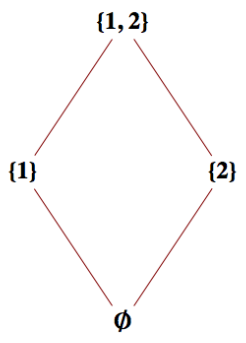
La Figura 6.2.4 es la gráfica para la relación de “contención establecida” en el conjunto de potencia de$\{1,2\}\text{.}$

La Figura 6.2.4 es útil en la medida en que nos recuerda que cada conjunto es un subconjunto de sí mismo y nos muestra de un vistazo la relación entre los diversos subconjuntos en$\mathcal{P} (\{1,2\})\text{.}$ Sin embargo, cuando una relación es un ordenamiento parcial, podemos agilizar una gráfica como esta. La forma aerodinámica de un gráfico se llama diagrama Hasse o diagrama de orden. Un diagrama de Hasse toma en cuenta los siguientes hechos.

Por la propiedad reflexiva, cada vértice debe estar relacionado consigo mismo, por lo que las flechas de un vértice a sí mismo (llamadas “auto-bucles”) no se dibujan en un diagrama de Hasse. Simplemente se asumen.
Por la propiedad antisimetría, las conexiones entre dos elementos distintos en una gráfica dirigida solo pueden ir en una dirección, si acaso. Cuando hay una conexión, acordamos colocar siempre el segundo elemento por encima del primero (como lo hacemos anteriormente con la conexión de$\{1\}$ a$\{1,2\}$). Por esta razón, podemos simplemente dibujar una conexión sin una flecha, solo una línea.
Por la propiedad transitiva, si hay aristas que conectan un elemento hasta un segundo elemento y el segundo elemento hasta un tercer elemento, entonces habrá una conexión directa del primero al tercero. Esto lo vemos en la Figura 6.2.4 con$\emptyset$ conectado a$\{1\}$ y luego$\{1\}$ conectado a$\{1,2\}\text{.}$ Notar el borde conectando$\emptyset$ a$\{1,2\}\text{.}$ Siempre que identifiquemos esta situación, retire la conexión de la primera a la tercera en un diagrama de Hasse y simplemente observar que una trayectoria ascendente de cualquier longitud implica que el elemento inferior está relacionado con el superior.

Usando estas observaciones como guía, podemos dibujar un diagrama de Hasse para$\subseteq$ on$\{1,2\}$ como en la Figura$\PageIndex{1}$.

Ejemplo$\PageIndex{2}$: Definition of a Relation using a Hasse Diagram

Considere la relación de orden parcial$s$ cuyo diagrama de Hasse es Figura$\PageIndex{2}$.

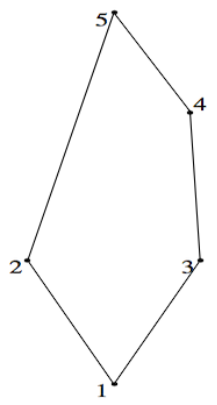
¿Cómo leemos este diagrama? Qué es$A\text{?}$ ¿$s\text{?}$Qué es ¿Cómo se$s$ ve el dígrafo de? Ciertamente$A = \{1,2,3,4,5\}$ y$1 s 2\text{,}$$3 s 4\text{,}$$1 s 4\text{,}$$1 s 5\text{,}$ etc., Observe que$1 s 5$ está implícito por el hecho de que hay un camino de longitud tres hacia arriba de 1 a 5. Esto se desprende de los bordes que se muestran y la propiedad transitiva que se presume en un poset. Desde$1 s 3$ y$3 s 4\text{,}$ sabemos que luego$1 s 4\text{.}$ nos combinamos$1 s 4$ con$4 s 5$ para inferir$1 s 5\text{.}$ Sin entrar en detalles por qué, aquí hay una lista completa de pares definidos por$s\text{.}$

\ begin {ecuación*} s =\ {(1,1), (2,2), (3,3), (4,4), (5,5), (1,3), (1,4), (1,5), (1,2), (3,4), (3,5), (4,5), (2,5)\}\ final {ecuación*}

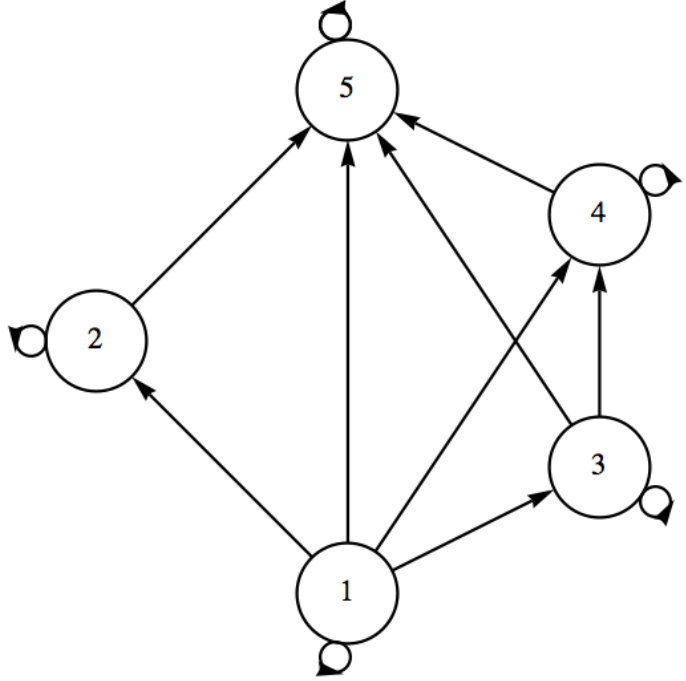
Un dígrafo para$s$ es Figura$\PageIndex{3}$. Sin duda es más complicado de leer y difícil de dibujar que el diagrama de Hasse.

Un ejemplo clásico de una relación de ordenación parcial está$\leq $ en los números reales,$\mathbb{R}\text{.}$ De hecho, al graficar relaciones de ordenación parcial, es natural “trazar” los elementos desde el poset dado comenzando con el elemento “menor” al “mayor” y usar términos como “menos”, “mayor”, etc. porque de esto se debe advertir al lector que algunos textos utilizan el símbolo$\leq$ para ordenamientos parciales arbitrarios. Esto puede resultar bastante confuso para el novato, así que seguimos usando letras genéricas$r\text{,}$$s\text{,}$ etc.

Relaciones de equivalencia

Otra propiedad común de las relaciones es la simetría.

Definición$\PageIndex{5}$: Symmetric Relation

Dejar$r$ ser una relación en un conjunto$A\text{.}$$r$ es simétrica si y sólo si cada vez$a r b\text{,}$ que sigue eso$b r a\text{.}$

Considerar la relación de igualdad definida en cualquier conjunto$A\text{.}$ Ciertamente$a = b$ implica que$b = a$ así la igualdad es una relación simétrica sobre$A\text{.}$

Sorprendentemente, la igualdad es también una relación antisimétrica sobre$A\text{.}$ Esto se debe a que la condición que define la propiedad antisimetría,$a = b$ y$a \neq b\text{,}$ es una contradicción. Recuerde, una proposición condicional siempre es cierta cuando la condición es falsa. ¡Entonces una relación puede ser simétrica y antisimétrica en un set! Nuevamente recordemos que estos términos no son negativos unos de otros. Dicho esto, hay muy pocas relaciones importantes distintas de la igualdad que sean simétricas y antisimétricas.

Definición$\PageIndex{6}$: Equivalence Relation

Una relación$r$ en un conjunto$A$ se llama relación de equivalencia si y solo si es reflexiva, simétrica y transitiva.

El ejemplo clásico de una relación de equivalencia es la igualdad en un conjunto$A\text{.}$ De hecho, se utiliza el término relación de equivalencia porque aquellas relaciones que satisfacen la definición se comportan bastante como la relación de igualdad. Aquí hay otra relación de equivalencia importante.

Ejemplo$\PageIndex{3}$: Equivalent Fractions

Dejado$\mathbb{Z}^*$ ser el conjunto de enteros distintos de cero. Una de las relaciones de equivalencia más básicas en matemáticas es la relación$q$ sobre$\mathbb{Z}\times \mathbb{Z}^*$ definida por$(a, b) q(c, d)$ si y sólo si$a d = b c\text{.}$ Vamos a dejarlo en manos del lector para, verificar que efectivamente$q$ es una relación de equivalencia. Tenga en cuenta que dado que los elementos de$\mathbb{Z}\times \mathbb{Z}^*$ son pares ordenados, probar simetría implica cuatro números y la transitividad involucra seis números. Dos pares ordenados,$(a, b)$ y$(c, d)\text{,}$ están relacionados si las fracciones$\frac{a}{b}$ y$\frac{c}{d}$ son numéricamente iguales.

Nuestro siguiente ejemplo involucra las siguientes relaciones fundamentales sobre el conjunto de enteros.

Definición $\PageIndex{7}$: Congruence Modulo $n$

Dejar$n$ ser un entero positivo,$n\geq 2\text{.}$ definimos congruencia módulo n para ser la relación$\equiv_n$ definida en los enteros por

\ begin {ecuación*} a\ equiv_n b\ Leftrightarrow n\ mid (a-b)\ end {ecuación*}

Observamos lo siguiente sobre congruencia módulo$n\text{:}$

Esta relación es reflexiva, por si$a \in \mathbb{Z} \text{,}$$n \mid (a-a) \Rightarrow a\equiv_n a \text{.}$
Esta relación es simétrica. Podemos demostrarlo a través de la siguiente cadena de implicaciones.
\ begin {ecuation*}\ begin {split} a\ equiv_n b &\ Rightarrow n\ mid (a-b)\\ &\ Rightarrow\ textrm {Para algunos} k\ in\ mathbb {Z}, a-b = n k\\ &\ Rightarrow b-a = n (-k)\ &\ Rightarrow n\ mid (b-a)\ &\ Fila derecha b\ equiv_n a\ end {split}\ text {.} \ end {ecuación*}
Por último, esta relación es transitiva. Dejamos que el lector demuestre que si$a \equiv _n b $ y$b\equiv _n c\text{,}$ luego$a \equiv _n c\text{.}$

Frecuentemente, verá la notación equivalente$a \equiv b (\textrm{mod } n)$ para módulo de congruencia$n\text{.}$

Ejemplo$\PageIndex{4}$: Random Relations Usually have No Properties

Considere las relaciones descritas por el dígrafo en la Figura$\PageIndex{4}$. Esto se creó seleccionando aleatoriamente si dos elementos de$\{a,b,c\}$ estaban o no relacionados o no. Convénzase de que lo siguiente es cierto:

Esta relación no es reflexiva.
No es antisimétrico.
Además, no es simétrico.
No es transitivo.
¿Es$s$ una relación de equivalencia o un ordenamiento parcial?

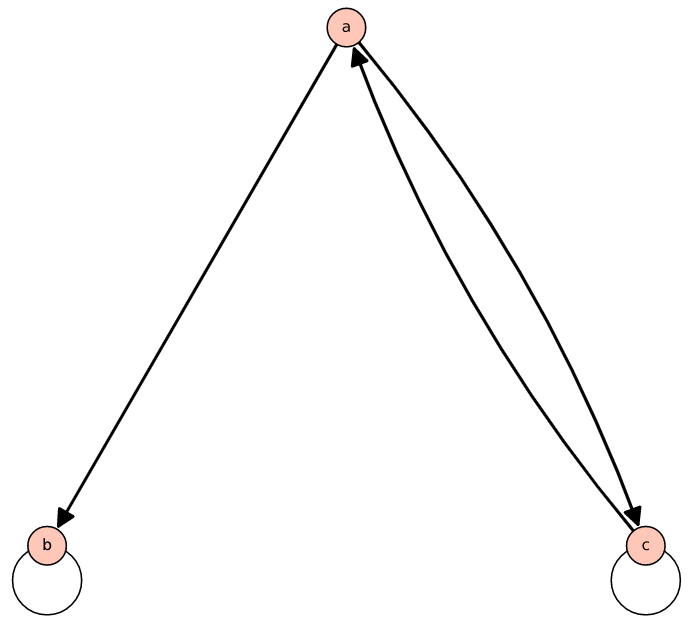
No todas las elecciones aleatorias de una relación serán tan totalmente negativas, pero a medida que aumenta el conjunto subyacente, la probabilidad de que alguna de las propiedades sea verdadera comienza a desaparecer.

Ejercicios

Ejercicio$\PageIndex{1}$

Deja$B = \{a, b\}$ y$U = \mathcal{P}(B)\text{.}$ dibuja un diagrama de Hasse para$\subseteq $$U\text{.}$
Let$A = \{1,2, 3, 6\}\text{.}$ Show que divide,$\mid \text{,}$ es un orden parcial en$A\text{.}$
Dibuja un diagrama de Hasse para dividir en$A\text{.}$
Compare las gráficas de las partes a y c.

Contestar

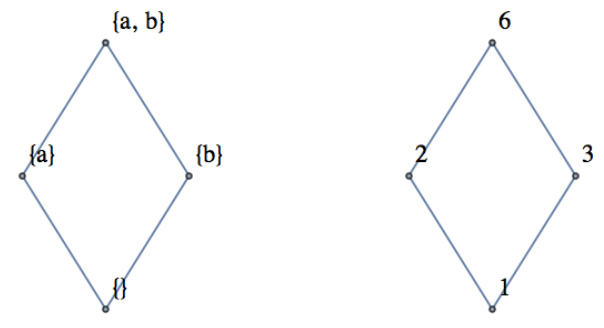
$clipboard_eea53c72faee8a3fd8aa14ce41d37ce7a.png$

Figura$\PageIndex{5}$

Ver Figura$\PageIndex{5}$.
Las gráficas son las mismas si hacemos caso omiso de los nombres de los vértices.

Ejercicio$\PageIndex{2}$

Repita el ejercicio$\PageIndex{1}$ con$B = \{a, b, c\}$ y$A = \{1, 2, 3, 5, 6, 10, 15, 30\}\text{.}$

Pista

Aquí hay un diagrama de Hasse para la parte (a).

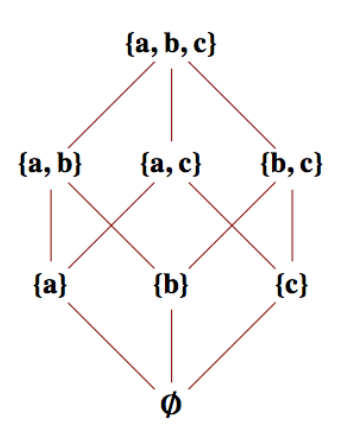
$clipboard_e0c0711bfa240b7ef85775aa360bd59b3.png$

Figura$\PageIndex{6}$: Diagrama de Hasse para un conjunto de contención para subconjuntos de un conjunto de tres elementos.

Ejercicio $\PageIndex{3}$

Considerar las relaciones definidas por los dígrafos en la Figura$\PageIndex{7}$.

Determinar si las relaciones dadas son reflexivas, simétricas, antisimétricas o transitivas. Tratar de desarrollar procedimientos para determinar la validez de estas propiedades a partir de las gráficas,
¿Cuáles de las gráficas son de relaciones de equivalencia o de ordenamientos parciales?

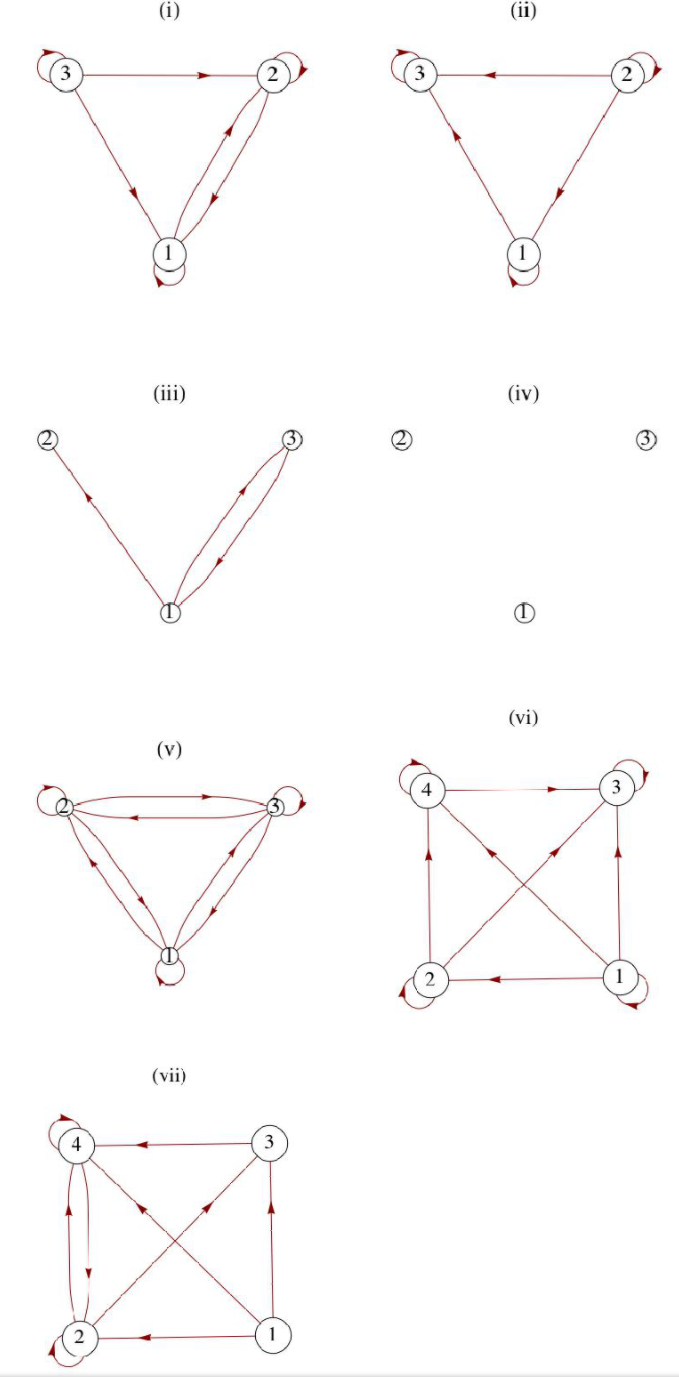
$clipboard_ec763040e9cb5e6bf01e346508eed79a9.png$

Figura$\PageIndex{7}$: Algunos dígrafos de relaciones

Contestar

Tabla$\PageIndex{1}$: Propiedades de las relaciones definidas por dígrafos

Parte	¿reflexivo?	¿simétrica?	¿antisimétricos?	transitivo?
i	si	no	no	si
ii	si	no	si	si
iii	no	no	no	no
iv	no	si	si	si
v	si	si	no	si
vi	si	no	si	si
vii	no	no	no	no

Ver Tabla$\PageIndex{1}$
Las gráficas ii y vi muestran relaciones parciales de ordenación. La gráfica v es de una relación de equivalencia.

Ejercicio$\PageIndex{4}$

Determine cuáles de las siguientes son relaciones de equivalencia y/o relaciones de orden parcial para los conjuntos dados:

$A = \{\textrm{ lines in the plane}\}\text{,}$y$r$ definido por$x r y$ si y solo si$x$ es paralelo a$y\text{.}$ Asumir que cada línea es paralela a sí misma.
$A = \mathbb{R}$y$r$ definido por$x r y$ si y solo si$\lvert x -y \rvert \leq 7\text{.}$

Ejercicio$\PageIndex{5}$

Considerar la relación sobre$\{1, 2, 3, 4, 5, 6\}$ definida por$r = \{(i,j):\enspace \lvert i - j\rvert = 2\}\text{.}$

¿Es$r$ reflexivo?
¿Es$r$ simétrico?
¿Es$r$ transitivo?
Dibuja una gráfica de$r\text{.}$

Contestar

No, ya que$\mid 1-1\mid =0\neq 2\text{,}$ for example
Sí, porque$\mid i-j\mid =$$\mid j-i\mid \text{.}$
No, desde$\mid 2-4\mid =2$ y$\mid 4-6\mid =2\text{,}$ pero$\mid 2-6\mid =4\neq 2\text{,}$ por ejemplo.
Ver Figura$\PageIndex{8}$

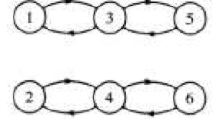
$clipboard_e4076c8c34be7921a3b9343a5a46a4fae.png$

Figura$\PageIndex{8}$

Ejercicio$\PageIndex{6}$

Para el conjunto de ciudades en un mapa, considere la relación$x r y$ si y sólo si ciudad$x$ está conectada por una carretera a ciudad Se considera que$y\text{.}$ una ciudad está conectada consigo misma, y dos ciudades están conectadas a pesar de que hay ciudades en la carretera entre ellas. ¿Es esto una relación de equivalencia o un ordenamiento parcial? Explique.

Ejercicio$\PageIndex{7}$: Equivalence Classes

Dejar$A = \{0, 1, 2, 3\}$ y dejar

\ begin {ecuación*} r =\ {(0, 0), (1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (3, 2), (2, 3), (3, 1), (1, 3)\}\ end {ecuación*}

Verificar que$r$ es una relación de equivalencia en$A\text{.}$
Let $a \in A$and define$c(a) = \{b \in A \mid a rb\}\text{.}$$c(a)$ se llama la clase de equivalencia de$a$ under$r$. Buscar$c(a)$ para cada elemento$a \in A\text{.}$
Mostrar que$\{c(a) \mid a \in A\}$ forma una partición de$A$ para este conjunto$A\text{.}$
Dejar$r$ ser una relación de equivalencia en un conjunto arbitrario$A\text{.}$ Probar que el conjunto de todas las clases de equivalencia bajo$r$ constituye una partición de$A\text{.}$

Contestar

$\displaystyle c(0)=\{0\}, c(1)=\{1,2,3\}=c(2)=c(3)$
$c(0)\cup c(1)=A$y$c(0)\cap c(1)=\emptyset$
Dejar$A$ ser cualquier conjunto y dejar$r$ ser una relación de equivalencia en$A\text{.}$ Let$a$ ser cualquier elemento de$A\text{.}$$a\in c(a)$ ya$r$ es reflexivo, por lo que cada elemento de$A$ está en alguna clase de equivalencia. Por lo tanto, la unión de todas las clases de equivalencia es igual$A\text{.}$ A continuación mostramos que dos clases de equivalencia cualesquiera son idénticas o disjuntas y ya terminamos. Dejar$c(a)$ y$c(b)$ ser dos clases de equivalencia, y asumir que$c(a)\cap c(b)\neq \emptyset\text{.}$ Queremos mostrar eso$c(a)=c(b)\text{.}$ Para mostrar que$c(a)\subseteq c(b)\text{,}$ dejar$x\in c(a)\text{.}$$x\in c(a) \Rightarrow a r x \text{.}$ También, existe un elemento,$y\text{,}$ de$A$ que está en la intersección de$c(a)$ y$c(b)$ por nuestra suposición. Por lo tanto,
\ begin {equation*}\ begin {split} a r y\ land b r y &\ Rightarrow a r y\ land y r b\ quad r\ textrm {es simétrico}\\ &\ Rightarrow a r b\ quad\ textrm {transitividad de} r\\ end {split}\ end {ecuación*}
Siguiente,
\ begin {ecuación*}\ begin {split} a r x\ land a r b &\ Rightarrow x r a\ land a r b\\ &\ Rightarrow x r b\\ &\ Rightarrow b r x\ &\ Rightarrow x\ in c (b)\\ end {split}\ end {equation*}
Del mismo modo,$c(b)\subseteq c(a)\text{.}$$\square$

Ejercicio$\PageIndex{8}$

Definir$r$ en el conjunto de potencia de$\{1, 2, 3\}$ por$A r B \Leftrightarrow \lvert A \rvert = \lvert B \rvert \text{.}$ Probar que$r$ es una relación de equivalencia. ¿Cuáles son las clases de equivalencia bajo$r\text{?}$

Ejercicio$\PageIndex{9}$

Considera las siguientes relaciones sobre$\mathbb{Z}_8= \{0, 1, . . . , 7\}\text{.}$ ¿Cuáles son las relaciones de equivalencia? Para las relaciones de equivalencia, enumere las clases de equivalencia.

$a r b$iff las ortografías inglesas de$a$ y$b$ comienzan con la misma letra.
$a s b$iff$a - b$ es un entero positivo.
$a t b$iff$a-b$ es un número entero par.

Contestar

Relación de equivalencia,$c(0)=\{0\},c(1)=\{1\},c(2)=\{2,3\} =c(3),c(4)=\{4,5\}=c(5)\text{,}$ y$c(6)=\{6,7\}=c(7)$
No es una relación de equivalencia.
Relación de equivalencia,$c(0)=\{0,2,4,6\}=c(2)=c(4)=c(6)$ y$c(1)=\{1,3,5,7\}=c(3)=c(5)=c(7)$

Ejercicio$\PageIndex{10}$

Sobre la base del ejercicio$\PageIndex{7}$:

Demostrar que el módulo de congruencia$m$ es transitivo.
¿Cuáles son las clases de equivalencia bajo congruencia módulo 2?
¿Cuáles son las clases de equivalencia bajo congruencia módulo 10?

Ejercicio$\PageIndex{11}$

En este ejercicio, demostramos que la implicación es un ordenamiento parcial. $A$Sea cualquier conjunto de proposiciones.

Verificar que$q \to q$ es una tautología, mostrando con ello que$\Rightarrow$ es una relación reflexiva sobre$A\text{.}$
Demostrar que$\Rightarrow$ es antisimétrico en$A\text{.}$ Nota: no usamos = al hablar de proposiciones, sino equivalencia,$\Leftrightarrow\text{.}$
Demostrar que$\Rightarrow$ es transitivo en$A\text{.}$
Dado que$q_i$ es la proposición$n < i$ sobre$\mathbb{N}\text{,}$ dibujar el diagrama de Hasse para la relación$\Rightarrow$ sobre$\{q_1, q_2, q_3,\ldots \}\text{.}$

Contestar

La prueba se desprende de la equivalencia bicondicional en el Cuadro 3.4.3.
Aplicar la regla de la cadena.
Ver Figura$\PageIndex{9}$.

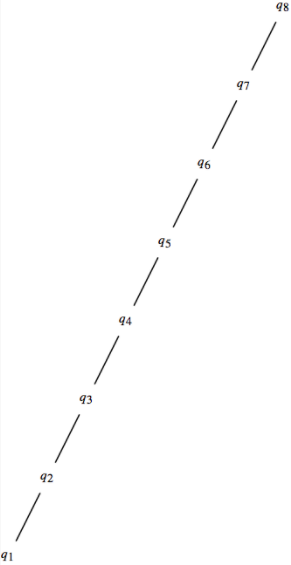
$clipboard_e07248c7b537d407b3f6ebf82e73eb89d.png$

Figura$\PageIndex{9}$

Ejercicio$\PageIndex{12}$

Deja$S = \{1,2,3,4,5,6,7\}$ ser un poset$(S, \leq )$ con el diagrama de Hasse que se muestra a continuación. Otra relación$r \subseteq S\times S$ se define de la siguiente manera:$(x, y) \in r$ si y solo si existe$z \in S$ tal que$z < x$ y$z < y$ en el poset$(S, \leq )\text{.}$

Demostrar que$r$ es reflexivo.
Demostrar que$r$ es simétrico.
Un compatible con respecto a la relación$r$ es cualquier subconjunto$Q$ de conjunto$S$ tal que$x \in Q \textrm{ and } y \in Q \Rightarrow (x, y) \in r\text{.}$ A compatible$g$ es un máximo compatible si no$Q$ es un subconjunto apropiado de otro compatible. Dar todos los máximos compatibles con respecto a la relación$r$ definida anteriormente.
Discutir una caracterización del conjunto de máximos compatibles para la relación$r$ cuando$(S, \leq )$ es un poset finito general. ¿Qué condiciones, en su caso, sobre un poset finito general$(S, \leq )$ harán$r$ una relación de equivalencia?

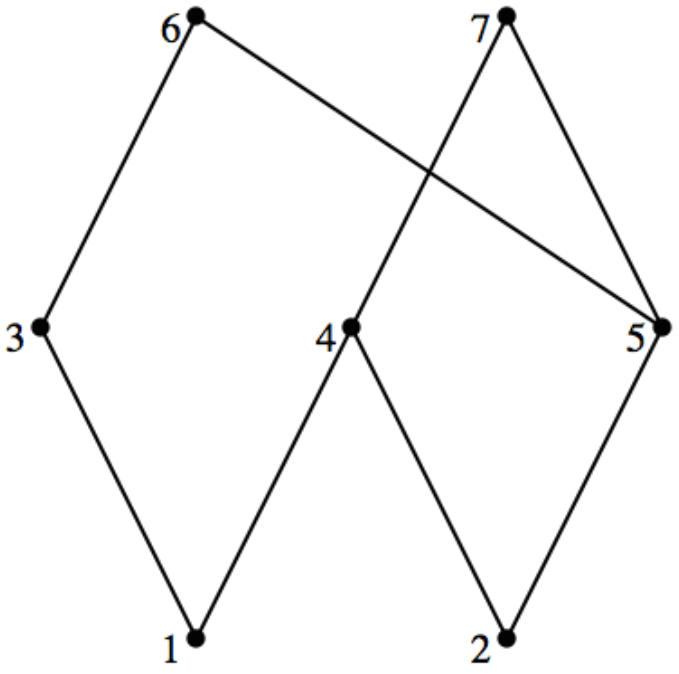
$clipboard_ec2ecb2fb41ad2732d2446753b2714ee8.png$

Figura$\PageIndex{10}$: Diagrama de Hasse para$r$ en Ejercicio$\PageIndex{12}$.