8.5: Generando funciones

Esta sección contiene una introducción al tema de generar funciones y cómo se utilizan para resolver las relaciones de recurrencia, entre otros problemas. Los métodos que emplean funciones generadoras se basan en el concepto de que se puede tomar un problema que involucra secuencias y traducirlo en un problema que implica generar funciones. Una vez que hayas resuelto el nuevo problema, una traducción de vuelta a secuencias te da una solución al problema original.

Esta sección abarca:

1. La definición de una función generadora.
2. Solución de una relación de recurrencia mediante funciones generadoras para identificar las habilidades necesarias para usar funciones generadoras.
3. Una introducción y/o revisión de las habilidades identificadas en el punto 2.
4. Algunas aplicaciones de generación de funciones.

Definición

Definición\(\PageIndex{1}\): Generating Function of a Sequence

La función generadora de una secuencia\(S\) con términos\(S_0,S_1 ,S_2, \dots \text{,}\) es la suma infinita

\ begin {ecuación*} G (S; z) =\ suma_ {n=0} ^ {\ infty} s_n z^n=s_0+s_1 z+s_2 z^2+s_3 z^3+\ cdots\ end {ecuación*}

El dominio y codominio de funciones generadoras no nos será de ninguna preocupación ya que solo estaremos realizando operaciones algebraicas sobre ellas.

Ejemplo\(\PageIndex{1}\): First Examples

1. Si\(S_n = 3^n\text{,}\)\(n \geq 0\text{,}\) entonces
   \ comienza {ecuación*}\ comienza {dividir} G (S; z) &= 1 + 3z + 9z^2 + 27z^3 +\ cdots\\ & =\ sum_ {n=0} ^ {\ infty} 3^n z^n\\ &=\ sum_ {n=0} ^ {\ infty} (3 z) ^n\\ end {split}\ end {equation*}
   Podemos obtener una expresión de forma cerrada para\(G(S;z)\) observando que\(G(S;z) - 3z G(S;z) = 1\text{.}\) por lo tanto,\(G(S;z) =\frac{1}{1-3 z}\text{.}\)
2. Las secuencias finitas tienen funciones generadoras. Por ejemplo, la secuencia de coeficientes binomiales\(\binom{n}{0} \text{,}\)\(\binom{n}{1} \text{,}\)\(\ldots\text{,}\)\(\binom{n}{n} \text{,}\)\(n \geq 1\) tiene función generadora
   \ begin {equation*}\ begin {split} G (\ binom {n} {\ cdot}; z) & =\ binom {n} {0} +\ binom {n} {1} z +\ cdots +\ binom {n} {n} z^n\ & =\ sum_ {k=0} ^ {\ infty}\ binom {n} {k } z^k\\ &= (1+z) ^n\\\ end {split}\ end {equation*}
   por aplicación de la fórmula binomial.
3. Si\(Q(n) = n^2\text{,}\)\(G(Q;z)=\sum_{n=0}^{\infty} n^2 z^n=\sum_{k=0}^{\infty} k^2 z^k\text{.}\) Tenga en cuenta que el índice que se utiliza en la suma no tiene significancia. También, tenga en cuenta que el límite inferior de la suma podría comenzar en 1 ya que\(Q(0)=0\text{.}\)

Solución de una relación de recurrencia mediante funciones generadoras

Ilustramos el uso de funciones generadoras resolviendo\(S(n) - 2S(n - 1) - 3S(n - 2) = 0\text{,}\)\(n \geq 2\text{,}\) con\(S(0) = 3\) y\(S(1) = 1\text{.}\)

1. Traducir la relación de recurrencia en una ecuación sobre la generación de funciones.
   Dejar\(V(n) = S(n) - 2S (n - 1) - 3S (n - 2)\text{,}\)\(n \geq 2\text{,}\) con\(V(0) = 0\) y\(V(1) = 0\text{.}\) Por lo tanto,
   \ comenzar {ecuación*} G (V; z) = 0 + 0z +\ sum_ {n=2} ^ {\ infty} (S (n) - 2S (n - 1) - 3S (n - 2)) z^n= 0\ end {ecuación*}
2. Resuelve para la función generadora de la secuencia desconocida,\(G(S;z) = \sum_{n=0}^{\infty} S_n z^n\text{.}\)
   \ begin {equation*}\ begin {split} 0 & =\ sum_ {n=2} ^ {\ infty} {(S (n) - 2S (n - 1) - 3 S (n - 2)) z^n}\\ & =\ sum_ {n=2} ^ {\ infty} {S (n) z^n-2}\ left (\ suma_ {n=2} ^ {\ infty} S (n-1) z^n\ derecha) -3\ izquierda (\ suma_ {n=2} ^ {\ infty} S (n-2) z^ n\ derecha)\ end {split}\ end {equation*} El examen
   cercano de las tres sumas anteriores muestra:
   1. \ begin {equation*}\ begin {split}\ sum_ {n=2} ^ {\ infty} s_n z^n &=\ sum_ {n=0} ^ {\ infty} s_n z^n - S (0) -S (1) z\\ &= G (S; z) -3-z\ end {split}\ end {equation*}
      desde\(S(0)=3\) y\(S(1)=1\text{.}\)
   2. \ begin {equation*}\ begin {split}\ sum_ {n=2} ^ {\ infty} S (n-1) z^n &=z\ izquierda (\ suma_ {n=2} ^ {\ infty} S (n-1) z^ {n-1}\ derecha)\\ & =z\ izquierda (\ sum_ {n=1} ^ {\ infty} S (n) z^n\ derecha)\\ & = z\ izquierda (\ suma_ {n=0} ^ {\ infty} S (n) z^n-S (0)\ derecha)\\ &= z (G (S; z) -3)\ end {split}\ end {ecuación*}
   3. \ begin {equation*}\ begin {split}\ sum_ {n=2} ^ {\ infty} S (n-2) z^n & = z^2\ left (\ sum_ {n=2} ^ {\ infty} S (n-2) z^ {n-2}\ right)\\ & =z^2g (S; z)\ end {split}\ end {ecuación*}
      Por lo tanto,
      \ comenzar {ecuación*}\ comenzar {dividir} & (G (S; z) -3-z) -2z (G (S; z) -3) -3z^2g (S; z) =0\\ &\ Rightarrow G (S; z) -2z G (S; z) -3z^2g (S; z) =3 - 5z\\ &\ Rightarrow G (S; z) =\ frac {3-5z} {1-2z-3z^2}\ end {split}\ end {equation*}
3. Determinar la secuencia cuya función generadora es la que obtuvimos en el Paso 2.

   Para nuestro ejemplo, necesitamos conocer un hecho general sobre la expresión de forma cerrada de una secuencia exponencial (una prueba se dará más adelante):

   \[\label{eq:1}T(n)=ba^{n},\: n\geq 0\Leftrightarrow G(T;z)=\frac{b}{1-az}\]

   Ahora bien, para reconocer\(S\) en nuestro ejemplo, debemos escribir nuestra expresión de forma cerrada para\(G(S;z)\) como una suma de términos como los\(G(T;z)\) anteriores. Tenga en cuenta que el denominador de se\(G(S;z)\) puede factorizar:

   \ begin {ecuación*} G (S; z) =\ frac {3-5z} {1-2z-3z^2} =\ frac {3-5z} {(1-3z) (1+z)}\ final {ecuación*}

   Si miras esta última expresión de\(G(S;z)\) cerca, puedes imaginar cómo podría ser el resultado de la suma de dos fracciones,

   \[\label{eq:2}\frac{3-5z}{(1-3z)(1+z)}=\frac{A}{1-3z}+\frac{B}{1+z}\]

   donde\(A\) y\(B\) son dos números reales que deben determinarse. Comenzando por la derecha de\(\eqref{eq:2}\), debe quedar claro que la suma, para cualquiera\(A\) y se\(B\text{,}\) vería como el lado izquierdo. El proceso de búsqueda de valores de\(A\) y\(B\) que hacen\(\eqref{eq:2}\) realidad se llama la descomposición de fracciones parciales del lado izquierdo:

   \ begin {ecuación*}\ begin {split}\ frac {A} {1-3z} +\ frac {B} {1+z} &=\ frac {A (1+z)} {(1-3z) (1+z)} +\ frac {B (1-3z)} {(1-3z) (1+z)}\\ & =\ frac {(A+B) + (A-3B) z} {(1-3z) (1+z)}\ end {split}\ end {ecuación*}

   Por lo tanto,

   \ begin {ecuation*}\ left\ {\ begin {array} {c} A+B=3\\ A-3B=-5\\\ end {array}\ right\}\ Rightarrow\ left\ {\ begin {array} {c} A=1\\ B=2\\ end {array}\ derecha\}\ fin {ecuación*}

   y

   \ begin {ecuación*} G (S; z) =\ frac {1} {1-3z} +\ frac {2} {1+z}\ end {ecuación*}

   Podemos aplicar\(\eqref{eq:1}\) a cada término de\(G(S;z)\text{:}\)

   • \(\frac{1}{1-3z}\)es la función generadora para\(S_1(n)=1\cdot 3^n= 3^n\)
   • \(\frac{2}{1+z}\)es la función generadora para\(S_2(n)=2(-1)^n\text{.}\)

   Por lo tanto,\(S(n)=3^n+ 2(-1)^n\text{.}\)

A partir de este ejemplo, vemos que hay varias habilidades que deben ser dominadas para poder trabajar con funciones generadoras. Debes ser capaz de:

1. Manipular expresiones de suma y sus índices (en el Paso 2).
2. Resolver ecuaciones algebraicas y manipular expresiones algebraicas, incluyendo descomposiciones parciales de funciones (Pasos 2 y 3).
3. Identificar secuencias con sus funciones generadoras (Pasos 1 y 3).

Primero nos concentraremos en la última habilidad, una competencia en las otras habilidades es producto de hacer tantos ejercicios y leer tantos ejemplos como sea posible.

Primero, identificaremos las operaciones en secuencias y en funciones generadoras.

Operaciones en Secuencias

Definición \(\PageIndex{2}\): Operations on Sequences

Dejar\(S\) y\(T\) ser secuencias de números y dejar\(c\) ser un número real. Definir\(S + T\text{,}\) la suma del producto escalar\(c S\text{,}\) el producto\(S T\text{,}\) la convolución\(S*T\text{,}\) la operación pop\(S\uparrow\) (leer “\(S\)pop”), y la operación de empuje\(S\downarrow\) (leer “\(S\)push”) a término para\(k \geq 0\) por

\[\label{eq:3}(S+T)(k)=S(k)+T(k)\]

\[\label{eq:4}(cS)(k)=cS(k)\]

\[\label{eq:5}(S\cdot T)(k)=S(k)T(k)\]

\[\label{eq:6}(S * T)(k)=\sum\limits_{j=0}^{k}S(j)T(k-j)\]

\[\label{eq:7}(S\uparrow )(k)=S(k+1)\]

\[\label{eq:8}(S\downarrow )(k)=\left\{\begin{array}{cl}0&\text{if }k=0 \\ S(k-1)&\text{if }k>0\end{array}\right.\]

Si uno imagina que una secuencia es una matriz con una fila y un número infinito de columnas,\(S + T\) y\(c S\) son exactamente como en adición matricial y multiplicación escalar. No hay similitud obvia entre las otras operaciones y las operaciones matriciales.

Las operaciones pop y push se pueden entender imaginando una secuencia para ser una pila infinita de números con\(S(0)\) en la parte superior,\(S(1)\) siguiente, etc., como en la Figura\(\PageIndex{1}\) a. La secuencia\(S\uparrow\) se obtiene “haciendo estallar” S (0) de la pila, dejando una pila como en la Figura\(\PageIndex{1}\) b, con S (1) en la parte superior, S (2) siguiente, etc. La secuencia\(S\downarrow\) se obtiene colocando un cero en la parte superior de la pila, dando como resultado una pila como en la Figura\(\PageIndex{1}\) c. Tenga en cuenta estas cifras cuando discutamos las operaciones de pop y push.

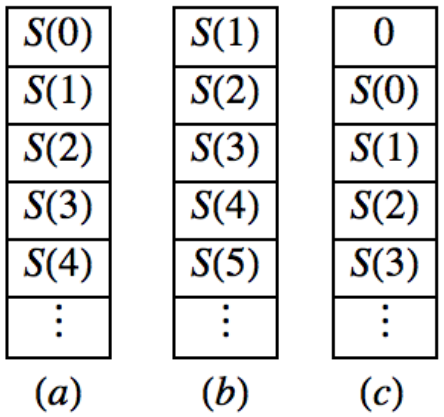Figura\(\PageIndex{1}\): Interpretación apilada de la orientación pop y push

Ejemplo\(\PageIndex{2}\): Some Sequence Operations

Si\(S(n) = n\text{,}\)\(T(n) = n^2\text{,}\)\(U(n) = 2^n\text{,}\) y\(R(n) =n 2^n\text{:}\)

1. \(\displaystyle (S + T)(n) = n + n^2\)
2. \(\displaystyle (U + R)(n) = 2^n+ n 2^n= (1+n)2^n\)
3. \(\displaystyle (2 U)(n) = 2\cdot 2^n= 2^{n+1}\)
4. \(\displaystyle \left(\frac{1}{2}R\right)(n)= \frac{1}{2}n 2^n= n 2^{n-1}\)
5. \(\displaystyle (S\cdot T)(n) = n n^2 = n^3\)
6. \(\displaystyle (S*T)(n)= \sum_{j=0}^n S(j) T(n-j)= \sum_{j=0}^n j (n-j)^2\\ \\ \quad \quad =\sum_{j=0}^n \left( j n^2-2 n j^2 + j^3\right)\\ \\ \quad \quad = n^2\sum_{j=0}^n j-2n \sum_{j=0}^n j^2 + \sum_{j=0}^n j ^3\\ \\ \quad \quad =n^{2 }\left(\frac{n (n+1)}{2}\right)- 2n\left(\frac{(2n+1)(n+1)n}{6}\right)+\frac{1}{4} n^2 (n+1)^2\\ \\ \quad \quad = \frac{n^2(n+1)(n-1)}{12}\)
7. \(\displaystyle (U*U)(n) =\sum_{j=0}^n U(j) U(n-j)\\ \\ \quad \quad =\sum_{j=0}^n 2^j 2^{n-j}\\ \\ \quad \quad = (n+1)2^n\)
8. \(\displaystyle (S\uparrow )(n)=n+1\)
9. \(\displaystyle (S\downarrow )(n)=\max (0,n-1)\)
10. \(\displaystyle ((S\downarrow )\downarrow )(n)= \max (0, n - 2)\)
11. \(\displaystyle (U\downarrow )(n)=\left\{ \begin{array}{cc} 2^{n-1} & \textrm{ if } n>0 \\ 0 & \textrm{ if } n=0 \\ \end{array} \right.\)
12. \(\displaystyle ((U\downarrow )\uparrow )(n)=(U\downarrow )(n+1)= 2^n= U(n)\)
13. \(\displaystyle ((U\uparrow )\downarrow ) (n)=\left\{ \begin{array}{cc} 0 & \textrm{ if } n = 0 \\ U(n) & \textrm{ if } n>0 \\ \end{array} \right.\)

Tenga en cuenta que\((U\downarrow )\uparrow \neq (U\uparrow )\downarrow\text{.}\)

Definición \(\PageIndex{3}\): Multiple Pop and Push

Si S es una secuencia de números y\(p\) un entero positivo mayor que 1, defina

\ begin {ecuación*} S\ uparrow p = (S\ uparrow (p - 1))\ uparrow\ quad\ textrm {if} p\ geq 2\ textrm {y} S\ uparrow 1 = S\ uparrow\ end {ecuación*}

Del mismo modo, defina

\ begin {ecuación*} S\ flecha abajo p = (S\ flecha abajo (p - 1))\ flecha abajo\ quad\ textrm {si} p\ geq 2\ textrm {y} S\ flecha abajo 1 = S\ flecha abajo\ fin {ecuación*}

En general,\((S \uparrow p)(k) = S(k+p),\) y

\ begin {ecuación*} (S\ flecha abajo p) (k) =\ left\ {\ begin {array} {cc} 0 &\ textrm {if} k < p\\ S (k-p) &\ textrm {if} k\ geq p\\ end {array}\\ right. \ end {ecuación*}

Operaciones en la generación de funciones

Definición\(\PageIndex{4}\): Operations on Generating Functions

Si\(G(z)=\sum_{k=0}^{\infty} a_k z^k\) y\(H(z) =\sum_{k=0}^{\infty} b_k z^k\) están generando funciones y\(c\) es un número real, entonces la suma\(G + H\text{,}\) escalar producto\(c G\text{,}\) producto\(G H\text{,}\) y producto monomial\(z^p G\text{,}\)\(p \geq 1\) están generando funciones, donde

\[\label{eq:9} (G+H)(z)=\sum\limits_{k=0}^\infty (a_{k}+b_{k})z^{k}\]

\[\label{eq:10}(cG)(z)=\sum\limits_{k=0}^\infty ca_{k}z^{k}\]

\[\label{eq:11}(GH)(z)=\sum\limits_{k=0}^\infty cz^{k}\text{ where }c_k=\sum\limits_{j=0}^k a_{j}b_{k-j}\]

\[\label{eq:12}(z^{p}G)(z)=z^{p}\sum\limits_{k=0}^\infty a_{k}z^{k}=\sum\limits_{k=0}^\infty a_{k}z^{k+p}=\sum\limits_{n=p}^\infty a_{n-p}z^n\]

La última suma se obtiene sustituyendo\(n - p\)\(k\) en la suma anterior.

Ejemplo\(\PageIndex{3}\): Some Operations on Generating Functions

Si\(D(z) =\sum_{k=0}^{\infty} kz^k\) y\(H(z) =\sum_{k=0}^{\infty} 2^k z^k\) entonces

\ begin {ecuación*} (D + H) (z) =\ suma_ {k=0} ^ {\ infty}\ izquierda (k+2 ^k\ derecha) z^k\ final {ecuación*}

\ begin {ecuación*} (2H) (z) =\ suma_ {k=0} ^ {\ infty} 2\ cdot 2^kz^k =\ suma_ {k=0} ^ {\ infty} 2^ {k+1} z^k\ end {ecuación*}

\ begin {equation*}\ begin {split} (z D) (z) &= z\ suma_ {k=0} ^ {\ infty} kz^k=\ sum_ {k=0} ^ {\ infty} kz^ {k+1}\\ &=\ sum_ {k=1} ^ {\ infty} (k-1) z^k = D (z) -\ sum_ {k=1} ^ {\ infty} (k-1) z^k = D (z) -\ sum_ _ {k=1} ^ {\ infty} z^k\\\ final {división}\ final {ecuación*}

\ begin {ecuación*} (D H) (z) =\ suma_ {k=0} ^ {\ infty}\ izquierda (\ suma_ {j=0} ^k j 2^ {k-j}\ derecha) z^k\ final {ecuación*}

\ begin {ecuación*} (H H) (z) =\ suma_ {k=0} ^ {\ infty}\ izquierda (\ suma_ {j=0} ^k 2^j2^ {k-j}\ derecha) z^k=\ sum_ {k=0} ^ {\ infty} (k+1) 2^k z^k\ end {ecuación*}

Nota:\(D(z) = G(S;z)\text{,}\) y\(H(z) = G(U;z)\) de Ejemplo\(\PageIndex{2}\).

Ahora establecemos la conexión entre las operaciones sobre secuencias y funciones generadoras. Dejar\(S\) y\(T\) ser secuencias y dejar\(c\) ser un número real.

\[\label{eq:13}G(S+T;z)=G(S;z)+G(T;z)\]

\[\label{eq:14}G(cS;z)=cG(S;z)\]

\[\label{eq:15}G(S*T;z)=G(S;z)G(T;z)\]

\[\label{eq:16}G(S\uparrow ;z)=(G(S;z)-S(0))/z\]

\[\label{eq:17}G(S\downarrow ;z)=zG(S;z)\]

En palabras,\(\eqref{eq:13}\) dice que la función generadora de la suma de dos secuencias es igual a la suma de las funciones generadoras de esas secuencias. Tómese el tiempo para escribir las otras cuatro identidades con sus propias palabras. De los ejemplos anteriores, estas identidades deberían ser bastante obvias, con la posible excepción de los dos últimos. Demostraremos\(\eqref{eq:16}\) como parte del siguiente teorema y dejaremos la prueba de\(\eqref{eq:17}\) al lector interesado. Obsérvese que no hay operación en la generación de funciones que esté relacionada con la multiplicación de secuencias; es decir,\(G(S\cdot T;z)\) no se puede simplificar.

Teorema\(\PageIndex{1}\): Generating Functions Related to Pop and Push

Si\(p > 1\text{,}\)

1. \(\displaystyle G(S\uparrow p;z) = \left(G(S;z) -\left.\sum_{k=0}^{p-1} S(k) z^k\right)/z^k\right.\)
2. \(G(S\downarrow p;z) = z^p G(S;z)\text{.}\)

Prueba

Demostramos (a) por inducción y dejamos la prueba de (b) al lector.

Bases:

\ begin {equation*}\ begin {split} G (S\ uparrow; z) &=\ sum_ {k=0} ^ {\ infty} S (k+1) z^k\\ & =\ sum_ {k=1} ^ {\ infty} S (k) z^ {k-1}\\ & =\ izquierda. \ izquierda (\ sum_ {k=1} ^ {\ infty} S (k) z^k\ derecha)\ derecha/z\\ & =\ izquierda. \ izquierda (S (0) +\ suma_ {k=1} ^ {\ infty} S (k) z^k-S (0)\ derecha)\ derecha/z\\ & = (G (S; z) -S (0)) /z\ end {split}\ end {ecuación*}

Por lo tanto, la parte (a) es cierta para\(p=1\text{.}\)

Inducción: Supongamos que para algunos\(p\geq 1\text{,}\) la afirmación en la parte (a) es cierta:

\ begin {ecuation*}\ begin {split} G (S\ uparrow (p+1); z) &= G ((S\ uparrow p)\ uparrow; z)\\ & = (G (S\ uparrow p; z) - (S\ uparrow p) (0)) /z\ textrm {por la base}\\ & =\ frac\ frac {\ left (G (S; z) -\ suma_ {k=0} ^ {p-1} S (k) z^k\ derecha)} {z^p} -S (p)} {z}\ end {split}\ end {ecuación*}

por la hipótesis de inducción. Ahora escribe\(S(p)\) en la última expresión anterior\(\left(S(p)z^p \right)/z^p\) para que encaje en la suma finita:

\ begin {ecuación*}\ begin {split} G (S\ uparrow (p+1); z) & =\ left. \ izquierda (\ frac {G (S; z) -\ suma_ {k=0} ^p S (k) z^k} {z^p}\ derecha)\ derecha/z\\ & =\ izquierda (G (S; z) -\ suma_ {k=0} ^p S (k) z^k\ derecha) /z^ {p+1}\ end {split}\ end {equ. *}

Por lo tanto, la afirmación es cierta para\(p+1\text{.}\)

Expresiones de formulario cerradas para generar funciones

La herramienta más básica utilizada para expresar funciones generadoras en forma cerrada es la expresión de forma cerrada para la serie geométrica, que es una expresión de la forma\(a + a r + a r^2+ \cdots\text{.}\) Puede ser terminada o extendida infinitamente.

Serie geométrica finita:

\[\label{eq:18}a+ar+ar^{2}+\cdots +ar^{n}=a\left(\frac{1-r^{n+1}}{1-r}\right)\]

Serie geométrica infinita:

\[\label{eq:19}a+ar+ar^{2}+\cdots =\frac{a}{1-r}\]

Restricciones:\(a\) y\(r\) representan constantes y los lados derechos de las dos ecuaciones se aplican bajo las siguientes condiciones:

1. \(r\)no debe ser igual a 1 en el caso finito. Tenga en cuenta que\(a + a r + \cdots a r^n = (n + 1)a\) si\(r = 1\text{.}\)
2. En el caso infinito, el valor absoluto de\(r\) debe ser inferior a 1.

Estas restricciones no entran en juego con la generación de funciones. Podríamos derivar\(\eqref{eq:18}\) señalando que si\(S(n) = a + a r +\cdots + a r^n\text{,}\)\(n > 0\text{,}\) entonces\(S(n) = r S(n - 1) + a\) (Ver Ejercicio 8.3.10 de la Sección 8.3). Se utilizó una derivación alternativa en la Sección 8.4. Daremos los mismos pasos para derivar\(\eqref{eq:19}\). Vamos\(x = a + a r + a r^2 + \cdots \text{.}\) Entonces

\ begin {ecuación*} r x =a r+ ar^2 +\ cdots = x- a\ Rightarrow x-rx=a\ Rightarrow x=\ frac {a} {1-r}\ end {ecuación*}

Ejemplo\(\PageIndex{4}\): Generating Functions Involving Geometric Sums

1. Si\(S(n) = 9\cdot 5^n\text{,}\)\(n \geq 0\text{,}\)\(G(S;z)\) es una serie geométrica infinita con\(a = 9\) y\(r = 5z\text{.}\) Por lo tanto,\(G(S;z) = \frac{9}{1 - 5z}\text{.}\)
2. Si\(T(n) = 4\text{,}\)\(n \geq\) 0, entonces\(G(T;z) = 4/(1 - z)\text{.}\)
3. Si\(U(n) = 3(-1)^n\text{,}\) entonces\(G(U;z) = 3/(1 + z)\text{.}\)
4. \(C(n) = S(n) + T(n) + U(n) = 9 \cdot 5^n + 4 + 3(-1)^n\text{.}\)Entonces
   \ comenzar {ecuación*}\ comenzar {dividir} G (C; z) & = G (S; z) + G (T; z) + G (U; z)\\ & =\ frac {9} {1-5z} +\ frac {4} {1-z} +\ frac {3} {1+z}\\ & = -\ frac {14 z^2+34z-34z-34z-16} {5 z^3-z^2-5 z+1}\ end {split}\ text {.} \ end {equation*}
   Dada la elección entre la última forma de\(G(C;z)\) y la suma anterior de tres fracciones, preferiríamos dejarla como una suma de tres funciones. Como vimos en un ejemplo anterior, una descomposición parcial de fracciones de una fracción como la última expresión requiere algún esfuerzo para producir.
5. Si\(G(Q;z) = 34/(2 - 3z)\text{,}\) entonces se\(Q\) puede determinar multiplicando el numerador y denominador por 1/2 para obtener\(\frac{17}{1-\frac{3}{2}z}\text{.}\) Reconocemos esta fracción como la suma de la serie geométrica infinita con\(a = 17\) y\(r = \frac{3}{2}z\text{.}\) Por lo tanto\(Q(n) = 17(3/2)^n\text{.}\)
6. Si\(G(A;z) = (1 + z)^3\), entonces nos expandimos\((1 + z)^3\) a\(1 + 3z + 3z^2 + z^{3}\). Por lo tanto\(A(0) = 1\text{,}\)\(A(1) = 3\)\(A(2)= 3\text{,}\)\(A(3) = 1\text{,}\) y, dado que no hay términos de mayor potencia,\(A(n) = 0\text{,}\)\(n \geq 4\text{.}\) Una forma más concisa de describir\(A\)\(\binom{n}{k} \) es\(A(k) = \binom{3}{k} \text{,}\) ya que se interpreta como 0 de\(k > n\text{.}\)

Tabla\(\PageIndex{1}\): Expresiones de forma cerrada de algunas funciones generadoras

Secuencia	Función generadora
\(S(k)=b a^k\)	\(G(S;z)=\frac{b}{1-a z}\)
\(S(k)=k\)	\(G(S;z)=\frac{z}{(1-z)^2}\)
\(S(k)=b k a^k\)	\(G(S;z)=\frac{a b z}{(1-a z)^2}\)
\(S(k) = \frac{1}{k!}\)	\(G(S;z)=e^z\)
\(S(k) = \left\{ \begin{array}{cc} \binom{n}{k} & 0\leq k\leq n \\ 0 & k>n \\ \end{array}\right.\)	\(G(S;z)=(1+z)^n\)

Ejemplo\(\PageIndex{5}\): Another Complete Solution

Resolver\(S(k) + 3S(k - 1) - 4S(k -2) = 0\text{,}\)\(k\geq 2\text{,}\) con\(S(0) = 3\) y\(S(1) = -2\text{.}\) La solución se derivará utilizando los mismos pasos que se utilizaron anteriormente en esta sección, con una variación.

1. Traducir a una ecuación sobre la generación de funciones. Primero, cambiamos el índice de la relación de recurrencia sustituyendo\(n + 2\) por\(k\text{.}\) El resultado es\(S(n + 2) + 3S(n + 1) - 4S(n) = 0\text{,}\)\(n \geq 0\text{.}\) Ahora, si\(V(n) = S(n + 2) + 3 S(n + 1) - 4S(n)\text{,}\) entonces\(V\) es la secuencia cero, que tiene una función generadora de cero. Además,\(V = S\uparrow 2+3(S\uparrow )-4 S\text{.}\) por lo tanto,
   \ begin {equation*}\ begin {split} 0 &= G (V; z)\\ & = G (S\ uparrow 2; z) + 3 G (S\ uparrow; z) - 4G (S; z)\\ & =\ frac {G (S; z) - S (0) - S (1) z} {z^2} +4\ frac {(G (S; z) - S (0))} {z} - 4G (S; z)\\ final {dividir}\ final {ecuación*}
2. Ahora queremos resolver la siguiente ecuación para\(G(S;z)\text{:}\)
   \ begin {ecuación*}\ frac {G (S; z) - S (0) - S (1) z} {z^2} +4\ frac {(G (S; z) - S (0))} {z} - 4G (S; z) = 0\ end {ecuación*}
   Multiplicar por\(z^2\):
   \ begin {ecuación*} G (S; z) - 3 + 2z + 3z (G (S; z) - 3) - 4z^2 G ( S; z) = 0\ end {ecuación*}
   Expandir y recopilar todos los términos que involucran\(G(S;z)\) en un lado de la ecuación:
   \ begin {ecuación*}\ begin {array} {c} G (S; z) + 3z G (S; z) - 4z^2 G (S; z) = 3 + 7z\\ left (1 + 3z - 4z^2\ right) G (S; z) = 3 + 7z\\ left (1 + 3z - 4z^2\ right) G (S; z;) = 3 + 7z\\\ end {array}\ end {ecuación*}
   Por lo tanto,
   \ start {ecuación*} G (S; z) =\ frac {3+7z} {1 + 3z - 4z^2}\ end {ecuación*}
3. Determinar S a partir de su función generadora. \(1 + 3z - 4z^2 = (1 + 4z) (1 - z)\)así una descomposición parcial de la fracción\(G(S;z)\) sería:
   \ begin {ecuación*}\ frac {A} {1+4z} +\ frac {B} {1-z} =\ frac {A z-a-4 B z-B} {(z-1) (4 z+1)} =\ frac {(A+B) + (4B-A) z} {(z-1) (4 z+1)}\ end {*}
   Por lo tanto,\(A + B = 3\) y\(4B - A = 7\text{.}\) La solución de este conjunto de ecuaciones es\(A = 1\) y\(B = 2\text{.}\)\(G(S;z)= \frac{1}{1+4z}+ \frac{2}{1-z}\text{.}\)
   \ begin {ecuación*}\ begin {array} {c}\ frac {1} {1+4z}\ textrm {es la función generadora de} S_1 (n) =( -4) ^n\ textrm {, y}\\\ frac {2} {1-z}\ textrm {es la función generadora de} S_2 (n) = 2 (1) n = 2\\\ end {array}\ end {ecuación*}
   En conclusión, ya que\(G(S;z) = G\left(S_1;z\right) + G\left(S _2;z\right)\text{,}\)\(S(n) = 2 + (-4)^n\text{.}\)

Ejemplo\(\PageIndex{6}\): An Application to Counting

Let\(A = \{a, b, c, d, e\}\) y let\(A^*\) ser el conjunto de todas las cadenas de longitud cero o más que se pueden hacer usando cada uno de los elementos de\(A\) cero o más veces. Por la regla generalizada de los productos, existen\(5^n\) cadenas que tienen longitud\(n\text{,}\)\(n\geq 0\text{,}\) Supongamos que ese\(X_n\) es el conjunto de cadenas de longitud\(n\) con la propiedad de que todos los\(a\)'s y\(b\)'s preceden a todos los\(c\)'s,\(d\)'s, y \(e\)'s. Así\(aaabde \in X_6\text{,}\) pero\(abcabc \notin X_6\text{.}\) Let\(R(n) =\lvert X_n \rvert\text{.}\) Una expresión de forma cerrada para se\(R\) puede obtener reconociendo\(R\) como la convolución de dos secuencias. Para ilustrar nuestro punto, consideraremos el cálculo de\(R(6)\text{.}\)

Tenga en cuenta que si una cadena\(X_6\text{,}\) le pertenece comienza con\(k\) caracteres de\(\{a, b\}\) y es seguida por\(6 - k\) caracteres de\(\{c, d, e\}\text{.}\) Let\(S(k)\) be el número de cadenas de\(a\)'s y\(b\)'s con longitud\(k\) y let\(T(k)\) ser el número de cadenas de \(c\)'s,\(d\)'s, y\(e\)'s con longitud\(k\text{.}\) Por la regla generalizada de los productos,\(S(k) = 2^k\) y\(T(k) = 3^k\text{.}\) Entre los hilos en\(X_6\) están los que comienzan con dos y\(a\)\(b\)'s y terminan con\(c\)'s,\(d\)'s, y\(e\) s. ahí son\(S(2)T(4)\) tales cadenas. Por la ley de adición,

\ start {ecuación*}\ lvert X_6\ rvert =R (6) =S (0) T (6) +S (1) T (5) +\ cdots +S (5) T (1) +S (6) T (0)\ end {ecuación*}

Obsérvese que el sexto término de R es el sexto término de la convolución de\(S\) con\(T\text{,}\)\(S*T\text{.}\) Pensar en la situación general por un tiempo y debería quedar claro que\(R =S*T\text{.}\) Ahora, nuestro curso de acción será:

1. Determinar las funciones generadoras de\(S\) y\(T\text{,}\)
2. \(G(T;z)\)Multiplicar\(G(S;z)\) y obtener\(G(S*T;z) = G(R;z)\text{,}\) y
3. Determinar\(R\) sobre la base de\(G(R;z)\text{.}\)

1. \(G(S;z) =\sum_{k=0}^{\infty} 2^k z^k=\frac{1}{1-2z}\), y\(G(T;z) =\sum_{k=0}^{\infty} 3^k z^k=\frac{1}{1-3z}\)
2. \(\displaystyle G(R;z) = G(S;z)G(T;z) = \frac{1}{(1-2z)(1-3z)}\)
3. Para reconocer\(R\) de\(G(R;z)\text{,}\) debemos hacer una descomposición parcial de fracciones:
   \ begin {ecuation*}\ frac {1} {(1-2z) (1-3z)} =\ frac {A} {1-2z} +\ frac {B} {1-3z} =\ frac {-3 A z+a-2 B z+b} {(2 z-1) (3 z-1)} =\ frac {(A+B) + (-3 A -2 B) z} {(2 z-1) (3 z-1)}\ final {ecuación*}
   Por lo tanto, \(A + B = 1\)y\(-3A - 2B = 0\text{.}\) La solución de este par de ecuaciones es\(A = - 2\) y\(B = 3\text{.}\) Dado\(G(R;z) =\frac{-2}{1-2z}+\frac{3}{1-3z}\text{,}\) que es la suma de las funciones generadoras de\(-2(2)^k\) y\(3 (3)^k\text{,}\)\(R(k) =-2(2)^k+3 (3)^k = 3^{k+1}-2^{k+1}\)
   Por ejemplo,\(R(6) = 3^7 - 2^7= 2187 - 128 = 2059\text{.}\) Naturalmente, esto equivale a la suma que obtenemos de\((S*T)(6)\text{.}\) Para poner este número en perspectiva, el número total de cadenas de longitud 6 sin restricciones es\(5^6=15625\text{,}\) y por\(\frac{2059}{15625}\approx 0.131776\text{.}\) lo tanto aproximadamente 13 por ciento de las cuerdas de longitud 6 satisfacen las condiciones del problema.

Extra para Expertos

El resto de esta sección está destinado a lectores que hayan tenido, o que tengan la intención de tomar, un curso de combinatoria. No aconsejamos que se incluya en un curso típico. El método que se utilizó en el ejemplo anterior es muy potente y puede ser utilizado para resolver muchos problemas en combinatoria. Cerramos esta sección con una descripción general de los problemas que se pueden resolver de esta manera, seguido de algunos ejemplos.

Considerar la situación en la que\(P_1\text{,}\)\(P_2\text{,}\)\(\ldots\text{,}\)\(P_m\) se encuentran\(m\) las acciones que se deben tomar, cada una de las cuales da como resultado un resultado bien definido. Para cada\(k = 1,2, . . . ,m\)\(X_k\) definir ser el conjunto de posibles resultados de\(P_k\). Supondremos que cada resultado puede ser cuantificado de alguna manera y que la cuantificación de los elementos de\(X_k\) está definida por la función\(Q_k : X_k \to \{0, 1,2, . . .\}\text{.}\) Así, cada resultado tiene asociado un entero no negativo. Finalmente, definir una función de frecuencia\(F_k : \{0, 1, 2, . . .\} \to \{0, 1, 2, . . .\}\) tal que\(F_k(n)\) sea el número de elementos de los\(X_k\) que tienen una cuantificación de\(n\text{.}\)

Ahora, con base en estos supuestos, podemos definir los problemas que se pueden resolver. Si un proceso\(P\) se define como una secuencia de acciones\(P_1,P_2,\ldots ,P_m\) como la anterior, y si el resultado del\(P\text{,}\) cual sería un elemento de\(X_1\times X_2\times \cdots \times X_m\text{,}\) se cuantifica por

\ begin {ecuación*} Q\ left (a_1, a_2,\ ldots, a_m\ right) =\ suma_ {k=1} ^m Q_k\ left (a_k\ right)\ end {ecuación*}

entonces la función de frecuencia,\(F\text{,}\) porque\(P\) es la convolución de las funciones de frecuencia para las\(P_1\text{,}\)\(P_2\text{,}\)\(\ldots\text{,}\)\(P_m\text{,}\) cuales tiene una función generadora igual al producto de las funciones generadoras de las funciones de frecuencia\(F_1\text{,}\)\(F_2\text{,}\)\(\ldots\text{,}\)\(F_m\text{.}\) Es decir,

\ begin {ecuación*} G (F; z) =G\ izquierda (F_1; z\ derecha) G\ izquierda (F_2; z\ derecha)\ cdots\ izquierda (F_m; z\ derecha)\ final {ecuación*}

Ejemplo\(\PageIndex{7}\): Rolling Two Dice

Supongamos que enrolla un dado dos veces y suma los números en la cara superior para cada rollo. Dado que las caras del dado representan los enteros del 1 al 6, la suma debe estar entre 2 y 12. ¿De cuántas formas se puede obtener alguna de estas sumas? Obviamente, 2 solo se puede obtener de una manera, con dos 1's Hay dos secuencias que arrojan una suma de 3:1-2 y 2-1. Para obtener todas las frecuencias con las que se pueden obtener los números del 2 al 12, configuramos la situación de la siguiente manera. Porque\(j = 1, 2\text{;}\)\(P_j\) es el balanceo del dado por el\(j^{\text{th}}\) momento. \(X_j = \{1, 2, . . . , 6\}\)y\(Q_j : X_j \rightarrow \{0, 1, 2, 3,\ldots \}\) se define por\(Q_j(x) = x\text{.}\) Dado que cada número aparece en un dado exactamente una vez, la función de frecuencia es\(F_j(k)=1\) si\(1 \leq k \leq 6\text{,}\) y de\(F_j(k) = 0\) otra manera. El proceso de laminación de la matriz dos veces se cuantifica sumando el es\({Q_j}'s\text{;}\) decir,\(Q\left(a_1, a_2\right) =Q_{1}\left(a_1\right)+Q_2\left(a_2\right)\). La función de generación para la función de frecuencia de enrollar la matriz dos veces es entonces

\ begin {ecuación*}\ comenzar {dividir} G (F; z) & = G\ izquierda (F_1; z\ derecha) G\ izquierda (F_2; z\ derecha)\\ & = (z^6+z^5+z^4+z^3+z^2+z) ^2\\ & =z^ {12} +2 z^ {11} +3 z^ {10} +4 z^ 9+5 z^8+6 z^7+5 z^6+4 z^5+3 z^4+2 z^3+z^2\ end {split}\ end {equation*}

Ahora, para conseguir\(F(k)\text{,}\) acaba de leer el coeficiente de\(z^k\text{.}\) Por ejemplo, el coeficiente de\(z^5\) es 4, por lo que hay cuatro formas de rodar un total de 5.

Para aplicar este método, el paso crucial es descomponer un proceso grande de la manera adecuada para que se ajuste a la situación general que hemos descrito.

Ejemplo\(\PageIndex{8}\): Distribution of a Committee

Supongamos que una organización se divide en tres secciones geográficas, A, B y C. Supongamos que se debe seleccionar un comité ejecutivo de 11 miembros para que no más de 5 miembros de una sola sección estén en el comité y que las Secciones A, B y C deben tener mínimos de 3, 2 y 2 miembros, respectivamente, sobre el comité. Al observar únicamente el número de integrantes de cada sección del comité, ¿de cuántas formas se puede conformar el comité? Un ejemplo de comité válido serían 4 A, 4 B y 3 C's.

\(P_A\)Sea la acción de decidir cuántos integrantes (no quiénes) de la Sección A servirán en el comité. \(X_A= \{3, 4, 5\}\)y\(Q_A(k)=k\text{.}\) La función de frecuencia,\(F_A\), se define por\(F_A(k)=1\) si\(k\in X_k\), con\(F_A(k)=0\) lo contrario. \(G\left(F_A;z\right)\)es entonces\(z^3+ z^4+z^5\). De igual manera,\(G\left(F_B;z\right) =z^2+ z^3+ z ^4 + z^5= G\left(F_C ;z\right)\text{.}\) ya que el comité debe contar con 11 integrantes, nuestra respuesta será el coeficiente\(z^{11}\) en el\(G\left(F_A;z\right)G\left(F_B;z\right)G\left(F_C;z\right)\text{,}\) que se encuentre 10.

Ejercicios

Ejercicio\(\PageIndex{1}\)

¿Qué secuencias tienen las siguientes funciones generadoras?

1. \(1\)
2. \(\displaystyle \frac{10}{2-z}\)
3. \(\displaystyle 1 + z\)
4. \(\displaystyle \frac{3}{1+2z}+ \frac{3}{1-3z}\)

Contestar

1. \(\displaystyle 1,0,0,0,0,\ldots\)
2. \(\displaystyle 5(1/2)^k\)
3. \(\displaystyle 1,1,0,0,0,\ldots\)
4. \(\displaystyle 3(-2)^k+3\cdot 3^k\)

Ejercicio\(\PageIndex{2}\)

¿Qué secuencias tienen las siguientes funciones generadoras?

1. \(\displaystyle \frac{1}{1+z}\)
2. \(\displaystyle \frac{1}{4-3z}\)
3. \(\displaystyle \frac{2}{1-z}+ \frac{1}{1+z}\)
4. \(\displaystyle \frac{z+2}{z+3}\)

Ejercicio\(\PageIndex{3}\)

Buscar expresiones de forma cerrada para las funciones generadoras de las siguientes secuencias:

1. \(\displaystyle V(n) = 9^n\)
2. \(P\text{,}\)donde\(P(k) - 6 P(k - 1) + 5 P(k - 2) = 0\) para\(k \geq 2\text{,}\) con\(P(0) = 2\) y\(P(1) = 2\text{.}\)
3. La secuencia de Fibonacci:\(F(k + 2) = F(k + 1) + F(k)\text{,}\)\(k \geq 0\text{,}\) con\(F(0) = F(1) = 1\text{.}\)

Contestar

1. \(\displaystyle 1/(1-9z)\)
2. \(\displaystyle (2-10z)\left/\left(1-6z+5z^2\right)\right.\)
3. \(\displaystyle 1\left/\left(1-z-z^2\right)\right.\)

Ejercicio\(\PageIndex{4}\)

Buscar expresiones de forma cerrada para las funciones generadoras de las siguientes secuencias:

1. \(W(n) = \binom{5}{n} 2^n\)para\(0 \leq n \leq 5\) y\(W(n) = 0\) para\(n > 5\text{.}\)
2. \(Q\text{,}\)donde\(Q(k) + Q(k - 1) - 42Q(k - 2) = 0\) para\(k\geq 2\text{,}\) con\(Q(0) = 2\) y\(Q(1) = 2\text{.}\)
3. \(G\text{,}\)donde\(G(k + 3) = G(k + 2) + G(k + 1) + G(k)\) para\(k \geq 0\text{,}\) con\(G(0) = G(1) = G(2) = 1\text{.}\)

Ejercicio\(\PageIndex{5}\)

Para cada una de las siguientes expresiones, encontrar la descomposición parcial de la fracción e identificar la secuencia que tiene la expresión como una función generadora.

1. \(\displaystyle \frac{5+2z}{1-4z^2}\)
2. \(\displaystyle \frac{32-22z}{2-3z+z^2}\)
3. \(\displaystyle \frac{6-29z}{1-11z+ 30z^2}\)

Contestar

1. \(\displaystyle 3/(1-2z)+2/(1+2z), 3\cdot 2^k+2(-2)^k\)
2. \(\displaystyle 10/(1-z)+12/(2-z), 10+6(1/2)^k\)
3. \(\displaystyle -1/(1-5z)+7/(1-6z), 7\cdot 6^k-5^k\)

Ejercicio\(\PageIndex{6}\)

Encuentra las descomposiciones parciales de la fracción e identifica la secuencia que tiene las siguientes expresiones:

1. \(\displaystyle \frac{1}{1-9z^2}\)
2. \(\displaystyle \frac{1+3z}{16-8z+z^2}\)
3. \(\displaystyle \frac{2z}{1-6z-7z^2}\)

Ejercicio\(\PageIndex{7}\)

Dado eso\(S(k) = k\) y\(T(k) = 10k\text{,}\) cuál es el\(k^{\text{th}}\) término de la función generadora de cada una de las siguientes secuencias:

1. \(\displaystyle S + T\)
2. \(\displaystyle S\uparrow * T\)
3. \(\displaystyle S * T\)
4. \(\displaystyle S\uparrow *S\uparrow\)

Contestar

1. \(\displaystyle 11k\)
2. \(\displaystyle (5/3)k(k+1)(2k+1)+5k(k+1)\)
3. \(\underset{j=0}{\overset{k}{\Sigma }}(j)(10(k-j))=10k\underset{j=0}{\overset{k}{\Sigma }}j-10\underset{j=0}{\overset{k}{\Sigma }}j^2\)\(=5k^2(k+1)-(5k(k+1)(2k+1)/6) =(5/3)k(k+1)(2k+1)\)
4. \(\displaystyle k(k+1)(2k+7)/12\)

Ejercicio\(\PageIndex{8}\)

Dado eso\(P(k) = \binom{10}{k}\) y\(Q(k) = k!\text{,}\) cuál es el\(k^{\text{th}}\) término de la función generadora de cada una de las siguientes secuencias:

1. \(\displaystyle P * P\)
2. \(\displaystyle P + P\uparrow\)
3. \(\displaystyle P * Q\)
4. \(\displaystyle Q * Q\)

Ejercicio\(\PageIndex{9}\)

Un juego se juega rodando un dado cinco veces. Para la\(k^{\text{th}}\) tirada, se agrega un punto a tu puntaje si rotas un número superior a\(k\text{.}\) De lo contrario, tu puntaje es cero para esa tirada. Por ejemplo, la secuencia de rollos te\(2,3,4,1,2\) da una puntuación total de tres; mientras que una secuencia de 1,2,3,4,5 te da una puntuación de cero. De las\(6^5 = 7776\) posibles secuencias de rollos, ¿cuántas te dan una puntuación de cero? , de uno? \(\ldots \)de cinco?

Contestar

Coeficientes de\(z^0\) a través\(z^5\) de\((1+5z)(2+4z)(3+3z)(4+2z)(5+z)\)

\(\begin{array}{cc} k & \textrm{ Number of ways of getting a score of } k \\ 0 & 120 \\ 1 & 1044 \\ 2 & 2724 \\ 3 & 2724 \\ 4 & 1044 \\ 5 & 120 \\ \end{array}\)

Ejercicio\(\PageIndex{10}\)

Supongamos que enrolla un dado diez veces seguidas y registra el cuadrado de cada número que rueda. ¿De cuántas maneras podría la suma de los cuadrados de tus rollos equivaler a 40? ¿Cuál es el resultado más común?