9.1: Gráficas - Introducción General

Última actualización
Guardar como PDF

Page ID: 117157

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Definiciones

Recordemos que introdujimos las gráficas dirigidas en el Capítulo 6 como una herramienta para visualizar las relaciones en un conjunto. Aquí hay una definición formal.

Definición$\PageIndex{1}$: Simple Directed Graph

Un gráfico dirigido simple consiste en un conjunto no vacío de vértices$V\text{,}$ y un conjunto de aristas, es$E\text{,}$ decir, un subconjunto del conjunto$V \times V\text{.}$

Nota$\PageIndex{1}$: Some Terminology and Comments

Cada borde es un par ordenado de elementos del conjunto de vértices. La primera entrada es el vértice inicial del borde y la segunda entrada es el vértice terminal. A pesar de la terminología establecida en esta definición, muchas veces pensamos en una gráfica como una imagen, una ayuda para visualizar una situación. En el capítulo 6, introdujimos este concepto para ayudar a entender las relaciones en los sets. Si bien esas relaciones eran principalmente de naturaleza matemática, sigue siendo cierto que cuando vemos una gráfica, nos dice cómo los elementos de un conjunto están relacionados entre sí. Hemos optado por no permitir una gráfica con un conjunto de vértices vacíos, el llamado gráfico vacío. Hay tanto ventajas como desventajas al permitir la gráfica vacía, por lo que puede encontrarla en otras referencias.

Ejemplo$\PageIndex{1}$: A Simple Directed Graph

La figura$\PageIndex{1}$ es un ejemplo de una gráfica dirigida simple. En términos establecidos, esta gráfica es$(V, E)\text{,}$ donde$V = \{s, a, b\}$ y$E = \{(s, a), (s, b), (a, b), (b, a), (b,b)\}\text{.}$ Observe cómo cada borde está etiquetado ya sea 0 o 1. A menudo hay razones para etiquetar incluso gráficas simples. Algunas etiquetas son para ayudar a que una gráfica sea más fácil de discutir; otras son más significativas. Discutiremos el significado de las etiquetas en esta gráfica más adelante.

$clipboard_eccef2e5cef3635d52abc83cb3ea05d4b.png$ Figura $\PageIndex{1}$: Una gráfica dirigida

En ciertos casos puede haber una necesidad de más de un borde entre dos vértices, y necesitamos expandir la clase de gráficas dirigidas.

Definición$\PageIndex{2}$: Multigraph

Un multígrafo es un conjunto de vértices$V$ con un conjunto de aristas que pueden contener más de un borde entre los vértices.

Un punto importante a tener en cuenta es que si identificamos una gráfica como multigráfica, no es necesario que haya dos o más aristas entre algunos de los vértices. Sólo está permitido. En otras palabras, cada gráfica simple es un multígrafo. Esto es análogo a cómo un rectángulo es una figura geométrica más general que un cuadrado, pero un cuadrado todavía se considera un rectángulo.

Ejemplo$\PageIndex{2}$: A Multigraph

Una ocurrencia común de un multígrafo es una hoja de ruta. Las ciudades y pueblos del mapa pueden considerarse vértices, mientras que los caminos son los bordes. No es raro tener más de una carretera que conecte dos ciudades. Para dar indicaciones claras de viaje, nombramos o numeramos carreteras para que no haya ambigüedad. Utilizamos el mismo método para describir los bordes del multígrafo en la Figura$\PageIndex{2}$. No hay duda de qué$e3$ es; sin embargo, referirse al borde$(2, 3)$ sería ambiguo.

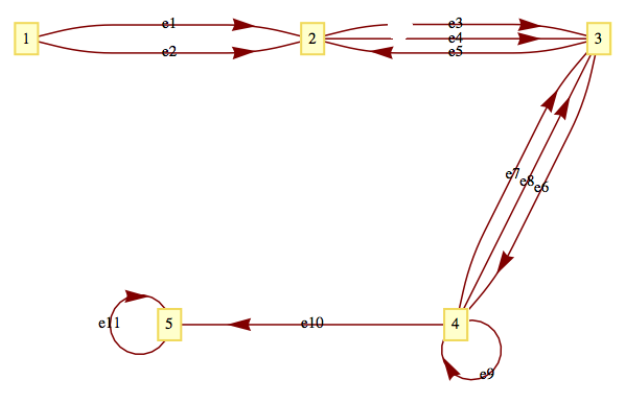$clipboard_e639156446172d612fc473b1d2f9d10bf.png$ Figura$\PageIndex{2}$: Un multígrafo dirigido

Hay casos en los que el orden de los vértices no es significativo y por lo tanto utilizamos un modelo matemático diferente para esta situación:

Definición$\PageIndex{3}$: Undirected Graph

Un gráfico no dirigido consiste en un conjunto no vacío$V\text{,}$ llamado conjunto de vértices, y un conjunto$E$ de subconjuntos de dos elementos$V\text{,}$ llamado conjunto de bordes. Los subconjuntos de dos elementos se dibujan como líneas que conectan los vértices. Es costumbre no permitir “self loops” en gráficas no dirigidas.

Nota$\PageIndex{2}$: On Empty Graphs

A algunos lectores se les puede ocurrir que una gráfica podría estar vacía, en el sentido de que tiene conjuntos de vértices y bordes vacíos. Podríamos referirnos a esta gráfica como la gráfica vacía. Sin embargo, no parece haber una definición universalmente acordada de una gráfica vacía. En algunas obras, una gráfica con cualquier número de vértices y sin aristas se denomina gráfica vacía. Para evitar este dilema, hemos definido gráficas tanto dirigidas como no dirigidas para que tengan conjuntos de vértices no vacíos. Por conveniencia, hemos relajado esta regla en nuestra definición de árbol enraizado, Definición 10.3.1, y permitido un árbol vacío.

Ejemplo $\PageIndex{3}$: An Undirected Graph

Una red de computadoras se puede describir fácilmente usando una gráfica. La figura$\PageIndex{3}$ describe una red de cinco computadoras,$a\text{,}$$b\text{,}$$c\text{,}$$d\text{,}$ y$e\text{.}$ Un borde entre dos vértices cualesquiera indica que la comunicación bidireccional directa es posible entre las dos computadoras. Tenga en cuenta que los bordes de esta gráfica no están dirigidos. Esto se debe a que la relación que se está mostrando es simétrica (es decir, si$X$ puede comunicarse con$Y\text{,}$ entonces$Y$ puede comunicarse con$X$). Aunque aquí se podrían usar bordes dirigidos, simplemente abarrotaría la gráfica.

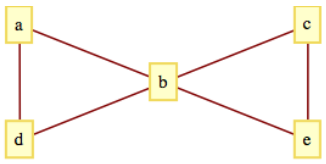$clipboard_e9169cfb99fc96ec348e6e45f25680882.png$ Figura$\PageIndex{3}$: Mapa de Comunicaciones

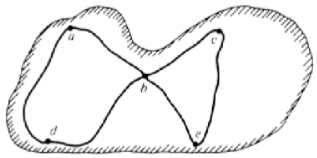$clipboard_e40bda6c3fa2613503566a44145d524c5.png$ Figura$\PageIndex{4}$: Mapa de carreteras de la isla

Esta gráfica no dirigida, en términos establecidos, es$V = \{a, b, c, d, e\}$ y$E = \{\{a, b\}, \{a, d\}, \{b, c\}, \{b, d\}, \{c, e\}, \{b, e\}\}$

Existen varias otras situaciones para las que esta gráfica puede servir como modelo. Una de ellas es interpretar los vértices como ciudades y los bordes como caminos, abstracción de un mapa como el de la Figura$\PageIndex{4}$. Otra interpretación es como una abstracción del plano de planta de una casa. Ver Ejercicio$\PageIndex{11}$. Vertex$a$ representa el exterior de la casa; todos los demás representan habitaciones. Dos vértices están conectados si hay una puerta entre ellos.

Definición $\PageIndex{4}$: Complete Undirected Graph

Una gráfica completa no dirigida sobre$n$ vértices es una gráfica no dirigida con la propiedad de que cada par de vértices distintos están conectados entre sí. Tal gráfico generalmente se denota por$K_n\text{.}$

Ejemplo$\PageIndex{4}$: A Labeled Graph

Un diagrama de flujo es un ejemplo común de una gráfica simple que requiere etiquetas para sus vértices y algunos de sus bordes. La figura$\PageIndex{5}$ es uno de esos ejemplos que ilustra cuántos problemas se resuelven.

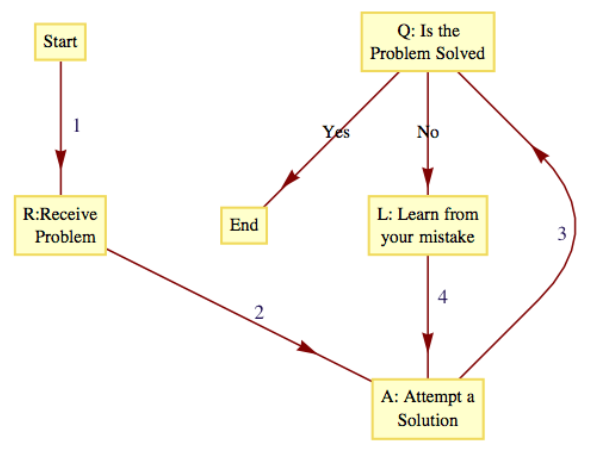$clipboard_ed2962e6675335af84e6d6cc754696746.png$ Figura$\PageIndex{5}$: Un diagrama de flujo - un ejemplo de una gráfica etiquetada

Al inicio del proceso de resolución de problemas, estamos en el vértice etiquetado como “Inicio” y al final (si tenemos la suerte de haber resuelto el problema) estaremos en el vértice etiquetado como “Fin”. La secuencia de vértices que atravesamos a medida que avanzamos de “Inicio” a “Fin” se llama camino. El vértice “Inicio” se llama el vértice inicial de la ruta, mientras que el “Fin” se llama el vértice final, o terminal,. Supongamos que el problema se resuelve después de dos intentos; entonces la ruta que se tomó es$\text{Start}, R, A, Q, L, A, Q, \text{End}\text{.}$ Una descripción de ruta alternativa sería enumerar los bordes que se utilizaron:$1, 2, 3, \text{No}, 4, 3, \text{Yes}\text{.}$ Este segundo método de describir una ruta tiene la ventaja de ser aplicable para multígrafos. En la gráfica de la Figura$\PageIndex{2}$, la lista de vértices$1,2,3,4,3$ no describe claramente una ruta entre 1 y 3, sino$e_1,e_4, e_6, e_7$ que es inequívoca.

Nota$\PageIndex{3}$: A Summary of Path Notation and Terminology

Si$x$ y$y$ son dos vértices de una gráfica, entonces un camino entre$x$ y$y$ describe un movimiento de$x$ a$y$ lo largo de los bordes de la gráfica. Vértice$x$ se llama el vértice inicial de la ruta y$y$ se llama vértice terminal. Una ruta entre$x$ y siempre$y$ puede ser descrita por su lista de bordes, la lista de aristas que se utilizaron:$\left(e_1, e_2, \ldots , e_n\right)\text{,}$ donde: (1) el vértice inicial de$e_1$ es$x\text{;}$ (2) el vértice terminal de$e_i$ es el vértice inicial de$e_{i+1}\text{,}$$i = 1, 2, \ldots , n - 1\text{;}$ y (3) el vértice terminal de$e_n$ es$y\text{.}$ El número de aristas en la lista de bordes es la longitud de la ruta. Una ruta en una gráfica simple también se puede describir mediante una lista de vértices. Una ruta de longitud$n$ tendrá una lista de$n + 1$ vértices$v_0=x\text{,}$$v_1\text{,}$$v_2,\ldots ,v_n=y\text{,}$ donde, for$k = 0,1,2,\ldots , n-1\text{,}$$\left(v_k,v_{k+1}\right)$ es un borde en la gráfica. Un circuito es un camino que termina en su vértice inicial.

Supongamos que una ruta entre dos vértices tiene una lista de bordes$(e_1, e_2 , . . . ,e_n)\text{.}$ Una subruta de esta gráfica es cualquier porción de la ruta descrita por uno o más bordes consecutivos en la lista de bordes. Por ejemplo,$(3, \textrm{No}, 4)$ es un subcamino de$(1,2,3, \textrm{No}, 4, 3, \text{Yes})\text{.}$ Cualquier camino es su propio subedero; sin embargo, lo llamamos un sub-camino impropio de sí mismo. Todas las demás subtrayectorias no vacías se denominan subtrayectorias adecuadas.

Una ruta o circuito es simple si no contiene una subruta adecuada que sea un circuito. Esto es lo mismo que decir que un camino o circuito es sencillo si no visita ningún vértice más de una vez a excepción del vértice inicial y terminal común en el circuito. En el método de resolución de problemas descrito en la Figura$\PageIndex{5}$, el camino que tomas es sencillo solo si llegas a una solución en el primer intento.

Subgrafías

Intuitivamente, probablemente podrías predecir qué significa el término “subgrafo”. Una gráfica contenida dentro de una gráfica, ¿verdad? Pero como una gráfica involucra dos conjuntos, vértices y aristas, ¿involucra un subconjunto de ambos conjuntos, o solo uno de ellos? La respuesta es que podría ser cualquiera. Existen diferentes tipos de subgrafos. Los dos que definiremos a continuación satisfarán la mayoría de nuestras necesidades futuras al discutir la teoría de las gráficas.

Definición $\PageIndex{5}$: Subgraph

Dejar$G=(V,E)$ ser una gráfica de cualquier tipo: dirigida, multigrafía dirigida, o no dirigida. $G'=(V',E')$es un subgrafo de$G$ si$V' \neq \emptyset\text{,}$$V' \subseteq V$ y$e \in E'$ solo si$e \in E$ y los vértices de$e$ están en$V'\text{.}$ Crea un subgrafo de$G$ eliminando cero o más vértices y todos los bordes que incluyen los vértices eliminados y luego posiblemente eliminas algún otro bordes.

Si los únicos bordes eliminados son aquellos que incluyen los vértices eliminados, entonces decimos que$G'$ es un subgrafo inducido. Por último,$G'$ es un subgrafo de expansión de$G$ si$V' = V\text{,}$ o, en otras palabras, no se eliminan vértices de$G\text{,}$ solo bordes.

Ejemplo$\PageIndex{5}$: Some Subgraphs

Considera la gráfica,$G\text{,}$ en la parte superior izquierda de la Figura$\PageIndex{6}$. Las otras tres gráficas en esa figura son todas subgráficas de$G\text{.}$ La gráfica en la parte superior derecha se creó eliminando primero el vértice 5 y todos los bordes conectándolo. Además, hemos eliminado el borde$\{1,4\}\text{.}$ Ese borde eliminado descalifica a la gráfica de ser una subgráfica inducida. Las gráficas en la parte inferior izquierda y derecha son ambas subgráficas que abarcan. El que está en la parte inferior derecha es un árbol, y se le conoce como un subárbol de expansión. Los subárboles abarcando serán discutidos en el Capítulo 10.

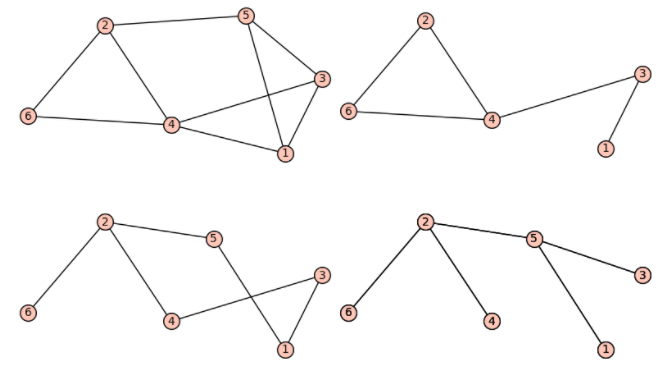$clipboard_e3e66644b02199d7d24e69e76c4c39fb8.png$ Figura$\PageIndex{6}$: Algunas subgráficas

Un conjunto de subgráficos de cualquier gráfica son los componentes conectados de una gráfica. Por simplicidad, los definiremos para gráficas no dirigidas. Dada una gráfica$G=(V,E)\text{,}$ consideramos la relación “está conectada a” on$V\text{.}$ Interpretamos esta relación para que cada vértice esté conectado consigo mismo, y cualesquiera dos vértices distintos están relacionados si hay un camino a lo largo de los bordes de la gráfica de uno a otro. No debería ser demasiado difícil convencerse de que esta es una relación de equivalencia en$V\text{.}$

Definición$\PageIndex{6}$: Connected Component

Dada una gráfica$G=(V,E)\text{,}$ deja$C$ ser la relación “está conectado a” on$V\text{.}$ Entonces los componentes conectados de$G$ son los subgráficos inducidos de$G$ cada uno con un conjunto de vértices que es una clase de equivalencia con respecto a$C\text{.}$

Ejemplo$\PageIndex{6}$

Si ignora los nombres duplicados de vértices en las cuatro gráficas de Figura$\PageIndex{6}$, y considera la figura completa como una gráfica grande, entonces hay cuatro componentes conectados en esa gráfica. ¡Es tan simple como eso! Es más difícil describir con precisión que entender el concepto.

De los ejemplos que hemos visto hasta ahora, podemos ver que aunque una gráfica puede definirse, en definitiva, como una colección de vértices y aristas, una parte integral de la mayoría de las gráficas es el etiquetado de los vértices y aristas que nos permite interpretar la gráfica como un modelo para alguna situación. Seguimos con algunos ejemplos más para ilustrar este punto.

Ejemplo$\PageIndex{7}$: A Graph as a Model for a Set of Strings

Supongamos que le gustaría describir mecánicamente el conjunto de cadenas de 0 y 1 que no tienen 1 consecutivos.Una forma de visualizar una cadena de este tipo es con la gráfica de la Figura$\PageIndex{1}$. Considere cualquier ruta que comience en el vértice$s\text{.}$ Si la etiqueta en cada gráfica se considera como la salida a una impresora, entonces la salida no tendrá 1 consecutivos.Por ejemplo, la ruta que es descrita por la lista de vértices$(s,a, b, b, a, b, b, a, b)$ resultaría en una salida de$10010010\text{.}$ Inversamente, cualquier cadena sin consecutivos 1's determina un camino que comienza en s.

Ejemplo$\PageIndex{8}$: A Tournament Graph

Supongamos que cuatro equipos compiten en un evento deportivo de todos contra todos; es decir, cada equipo se encuentra con cada otro equipo una vez, y cada juego se juega hasta que se determina un ganador. Si los equipos se llaman A, B, C y D, podemos definir la relación$\beta$ en el conjunto de equipos por$X \beta Y$ si$X$ vencieron$Y\text{.}$ Para un conjunto de resultados, la gráfica de$\beta$ podría verse como Figura$\PageIndex{7}$.

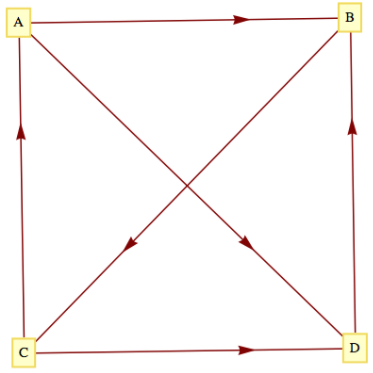$clipboard_e15459bdb37d2d16f411e8da34d06d74f.png$ Figura$\PageIndex{7}$: Gráfico de torneo round robin con cuatro vértices

Hay muchos tipos de torneos y todos pueden ser modelados por diferentes tipos de gráficas.

Definición$\PageIndex{7}$: Tournament Graph

Una gráfica de torneo es una gráfica dirigida con la propiedad de que ningún borde conecta un vértice consigo mismo, y entre dos vértices cualquiera hay como máximo un borde.
Un gráfico de torneo completo (o round robin) es un gráfico de torneo con la propiedad de que entre dos vértices distintos hay exactamente un borde.
Una gráfica de torneo de eliminación simple es una gráfica de torneo con las propiedades que: (i) un vértice (el campeón) no tiene borde que termine en él y al menos una arista iniciando desde él; (ii) cada dos vértices es el vértice terminal de exactamente un borde; y (iii) hay una trayectoria desde el vértice campeón hasta cada otro vértice.

Ejemplo$\PageIndex{9}$: Graph of a Single Elimination Tournament

El campeonato de beisbol de Grandes Ligas se decide con un torneo de eliminación simple, donde cada “juego” es en realidad una serie de juegos. De 1969 a 1994, los dos campeones divisionales de la Liga Americana (Este y Oeste) compitieron en una serie de juegos. El perdedor queda eliminado y el ganador compitió contra el ganador de la serie de la Liga Nacional (que se decide como en la Liga Americana). La gráfica del torneo del campeonato de 1983 se encuentra en la Figura$\PageIndex{8}$

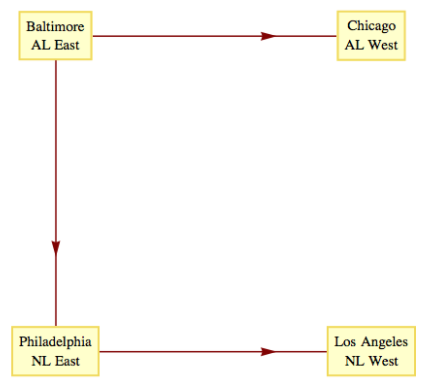$clipboard_e64195775f923acabf64da726f7dc1146.png$ Figura$\PageIndex{8}$: Un gráfico de torneo de eliminación simple

Gráfica Isomorfismos

A continuación, establecemos la relación “es isomórfica”, una forma de igualdad en las gráficas. Las gráficas de la Figura$\PageIndex{9}$ obviamente comparten algunas similitudes, como el número de vértices y el número de aristas. Ocurre que son aún más similares que solo eso. Si las letras$a\text{,}$$b\text{,}$$c\text{,}$ y$d$ en la gráfica izquierda se reemplazan por los números 1,3,4, y 2, respectivamente, y los vértices se mueven alrededor para que tengan la misma posición que la gráfica de la derecha, se obtiene la gráfica de la derecha.

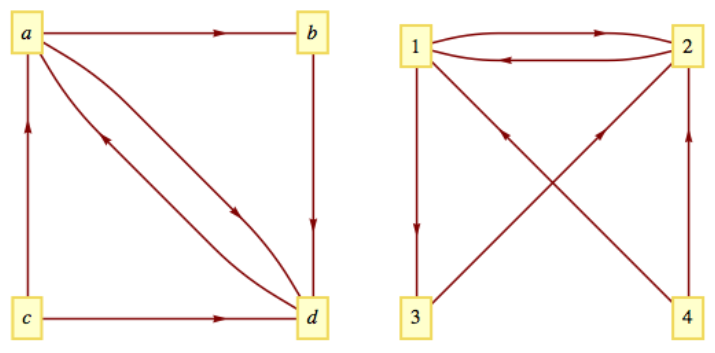$clipboard_e7698cd5b34cc85de270c6042dc77bfce.png$ Figura$\PageIndex{9}$: Gráficas isomórficas

Aquí hay una definición más precisa que refleja el hecho de que el posicionamiento real (o incrustación) de vértices no es una parte esencial de una gráfica.

Definición$\PageIndex{8}$: Isomorphic Graphs

Dos gráficas$(V, E)$ y$(V', E')$ son isomórficas si existe una biyección$f:V\to V'$ tal que$\left(v_i,v_j\right)\in E$ si y solo si$\left(f\left(v_i\right),f\left(v_j\right)\right)\in E'\text{.}$ Para multígrafos, agregamos que el número de aristas que se conectan$v_i$ a$v_j$ debe ser igual al número de aristas de$f\left(v_i\right)$ a$f\left(v_j\right)\text{.}$

La característica local más significativa de un vértice dentro de una gráfica es su grado. Colectivamente, los grados pueden caracterizar parcialmente una gráfica.

Definición $\PageIndex{9}$: Degree of a Vertex

Dejar$v$ ser un vértice de una gráfica no dirigida. El grado de$v\text{,}$ denotado$deg(v)\text{,}$ es el número de aristas$v$ que conectan con los otros vértices en la gráfica.
Si$v$ es un vértice de una gráfica dirigida, entonces el outdegree of$v\text{,}$ denotated$outdeg(v)\text{,}$ es el número de bordes de la gráfica que inician en$v\text{.}$ El indegree de$v\text{,}$ denotado$indeg(v)\text{,}$ es el número de aristas que terminan en$v\text{.}$

Definición$\PageIndex{10}$: Degree Sequence of a Graph

La secuencia de grados de una gráfica no dirigida es la secuencia no creciente de sus grados de vértice.

Ejemplo$\PageIndex{10}$: Some Degrees

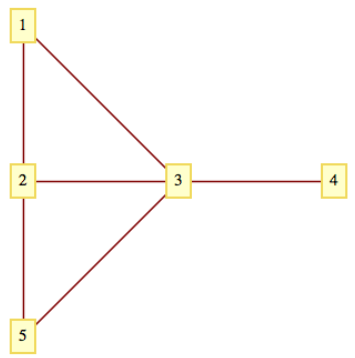$clipboard_e432b6310dcf1d9dfc6bc40f98874aa99.png$ Figura$\PageIndex{10}$: Una gráfica no dirigida

Los grados de vértices 1 a 5 en la Figura$\PageIndex{10}$ son 2, 3, 4, 1 y 2, respectivamente. La secuencia de grados de la gráfica es$(4,3,2,2,1)\text{.}$
En una gráfica de torneo,$outdeg(v)$ es el número de victorias para$v$ y$indeg(v)$ es el número de derrotas. En una gráfica de torneo completa (round-robin) con$n$ vértices,$outdeg(v)+ indeg(v) = n - 1$ para cada vértice.

Definición$\PageIndex{11}$: Graphic Sequence

Una secuencia finita no creciente de enteros$d_1,d_2, \ldots , d_n$ es gráfica si existe una gráfica no dirigida con$n$ vértices que tienen la secuencia como su secuencia de grados.

Por ejemplo,$4,2,1,1,1,1$ es gráfico porque los grados de la gráfica en la Figura$\PageIndex{11}$ coinciden con estos números. No hay conexión entre el número de vértice y su grado en esta gráfica.

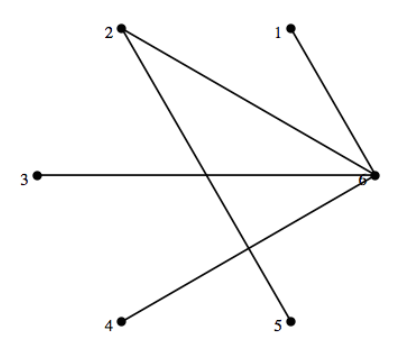$clipboard_e341ab7ed48c05837d42b8058c38f05d3.png$ Figura$\PageIndex{11}$: Una gráfica que muestra que$4,\: 2,\: 1,\: 1,\: 1,\: 1$ es una secuencia gráfica.

Ver [26] para más detalles sobre lo que también se conoce como secuencias gráficas de grados, incluyendo un algoritmo para determinar si una secuencia es gráfica o no.

Pasos

Lista$\PageIndex{1}$: A Prospectus for the Rest of the Chapter

La pregunta “Una vez que tienes una gráfica, ¿qué haces con ella?” podría venir a la mente. La siguiente lista de preguntas y comentarios comunes sobre las gráficas es una lista parcial que le dará una visión general del resto del capítulo.

¿Cómo se puede representar un gráfico como una estructura de datos para su uso en una computadora? Discutiremos algunas estructuras de datos comunes que se utilizan para representar gráficas en la Sección 9.2.
Dados dos vértices en una gráfica, ¿existe un camino entre ellos? La existencia de un camino entre cualquiera o todos los pares de vértices en una gráfica se discutirá en la Sección 9.3. Una pregunta relacionada es: ¿Cuántos caminos de cierto tipo o longitud hay entre dos vértices?
¿Hay un camino (o circuito) que pase a través de cada vértice (o utilice cada borde) exactamente una vez? Caminos de este tipo se llaman traversos. Discutiremos los recorridos en la Sección 9.4.
Supongamos que un costo está asociado con el uso de cada vértice y/o borde en una ruta. ¿Cuál es el camino, circuito o recorrido “más barato” de un tipo dado? Problemas de este tipo se discutirán en la Sección 9.5.
Dadas las especificaciones de una gráfica, o la propia gráfica, ¿cuál es la mejor manera de dibujar la gráfica? El deseo de pulcritud por sí solo hace de esta una pregunta razonable, pero hay otras motivaciones. Otro objetivo podría ser evitar que los bordes de la gráfica se crucen entre sí. Esto se discute en la Sección 9.6.

Ejercicios

Ejercicio$\PageIndex{1}$

¿Cuál es la significación del hecho de que existe un camino que conecta vértice$b$ con cada otro vértice en la Figura$\PageIndex{3}$, ya que se aplica a diversas situaciones que modela?

Contestar: En la Figura$\PageIndex{3}$, la computadora$b$ puede comunicarse con todas las demás computadoras. En Figura$\PageIndex{4}$, hay caminos directos hacia y desde la ciudad$b$ a todas las demás ciudades.

Ejercicio$\PageIndex{2}$

Dibuja una gráfica similar a la Figura$\PageIndex{1}$ que represente el conjunto de cadenas de 0 y 1 que no contengan más de dos 1 consecutivos en cualquier parte de la cadena.

Ejercicio$\PageIndex{3}$

Dibuja una gráfica dirigida que modele el conjunto de cadenas de 0 y 1 (cero o más de cada una) donde todas las 1 deben aparecer consecutivamente.

Contestar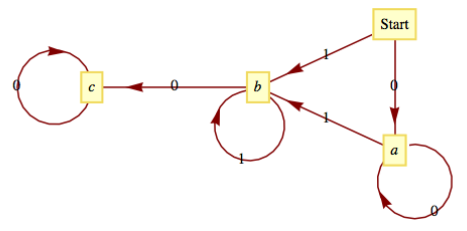: $clipboard_e9f23b4e75778bbd32d377559a42e7921.png$ Figura$\PageIndex{12}$: Solución al ejercicio$\PageIndex{3}$ de la Sección 9.1

Ejercicio$\PageIndex{4}$

En el torneo de básquetbol final-four de la NCAA, el campeón del Este juega al campeón del Oeste, y los campeones del Medio Oriente y Medio Oeste juegan. Los ganadores de los dos juegos juegan por el campeonato nacional. Dibuja las ocho gráficas diferentes de torneo de eliminación simple que podrían ocurrir.

Ejercicio$\PageIndex{5}$

¿Cuál es el número máximo de aristas en una gráfica no dirigida con ocho vértices?

Contestar: El número máximo de aristas sería$\binom{8}{2} = \frac{(7)(8)}{2}=28\text{.}$

Ejercicio$\PageIndex{6}$

¿Cuáles de las gráficas de la Figura$\PageIndex{13}$ son isomórficas? ¿Cuál es la correspondencia entre sus vértices?

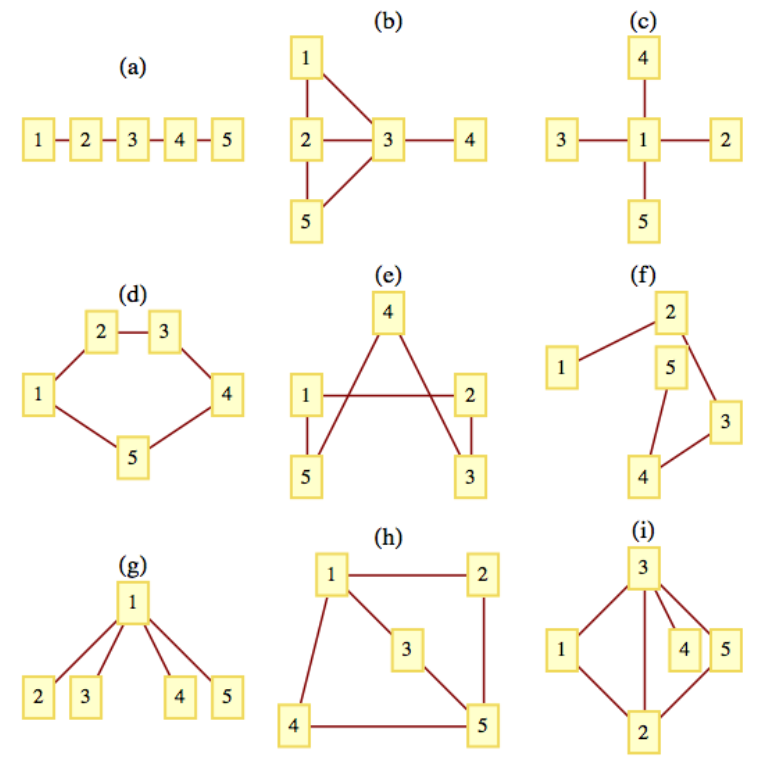$clipboard_e783f83042053c07abae0b4b93d37cd14.png$ Figura$\PageIndex{13}$: ¿Qué gráficas son isomórficas entre sí?

Ejercicio$\PageIndex{7}$

¿Cuántos bordes tiene una gráfica completa de torneo con$n$ vértices?
¿Cuántas aristas tiene una gráfica de torneo de eliminación simple con$n$ vértices?

Contestar

$\displaystyle \binom{n}{2}=\frac{(n-1)n}{2}$
$n-1\text{,}$cada vértice excepto el vértice campeón tiene un indegree de 1 y el vértice campeón tiene un indegree de cero.

Ejercicio$\PageIndex{8}$

Dibuja gráficas completas no dirigidas con 1, 2, 3, 4 y 5 vértices. ¿Cuántos bordes tiene$K_n\text{,}$ una gráfica completa no dirigida con$n$ vértices?

Ejercicio$\PageIndex{9}$

Determinar si las siguientes secuencias son gráficas. Explica tu lógica.

$\displaystyle (6, 5, 4, 3, 2, 1, 0)$
$\displaystyle (2,2,2,2,2,2)$
$\displaystyle (3,2,2,2,2,2)$
$\displaystyle (5,3,3,3,3,3)$
$\displaystyle (1,1,1,1,1,1)$
$\displaystyle (5,5,4,3,2,1)$

Contestar

No gráfico - si el grado de una gráfica con siete vértices es 6, está conectada a todos los demás vértices y así no puede haber un vértice con grado cero.
Gráfica. Una gráfica con esta secuencia de grados es un ciclo de longitud 6.
No gráfico. El número de vértices con grado impar es impar, lo cual es imposible.
Gráfica. Un “gráfico de rueda” con un vértice conectado a todos los demás y los demás conectados entre sí en un ciclo tiene esta secuencia de grados.
Gráfica. Pares de vértices conectados solo entre sí.
No gráfico. Con dos vértices teniendo grado máximo, 5, cada vértice necesitaría tener un grado de 2 o más, por lo que el 1 en esta secuencia lo hace no gráfico.

Ejercicio$\PageIndex{10}$

Con base en las observaciones que podrías haber hecho en Ejercicio$\PageIndex{9}$, describe tantas características como puedas sobre secuencias gráficas de longitud$n\text{.}$
Considera las dos gráficas de la Figura$\PageIndex{14}$. Observe que tienen las mismas secuencias de grado,$(2,2,2,2,2,2)\text{.}$ Explica por qué las dos gráficas no son isomórficas.

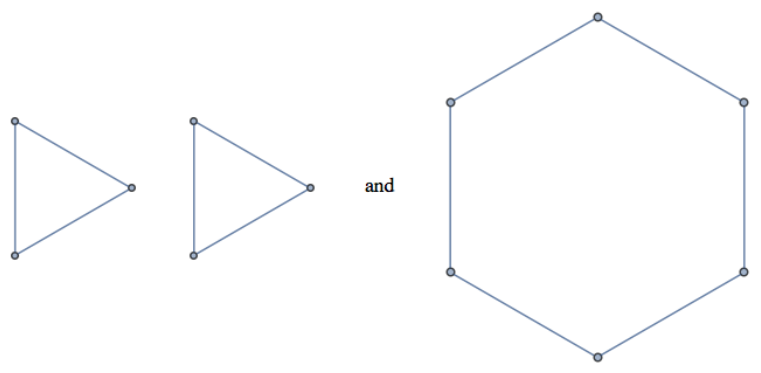$clipboard_ed1d6c040204fc91d9f1fe5288e4754f0.png$ Figura$\PageIndex{14}$: Dos gráficas con las mismas secuencias de grados

Ejercicio$\PageIndex{11}$

Dibujar un plano para las habitaciones de una casa para que la Figura$\PageIndex{3}$ modele la conectividad de las habitaciones. Es decir,$(a,b)$ es un borde si y solo si una puerta conecta habitaciones$a$ y$b\text{.}$

Ejercicio$\PageIndex{12}$

¿Cuántos subgráficos hay de un$K_n\text{,}$$n \geq 1\text{.}$ ¿Cuántos de ellos son gráficos abarcando?