9.2: Estructuras de Datos para Gráficas

Última actualización
Guardar como PDF

Page ID: 117158

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección, describiremos las estructuras de datos que se utilizan comúnmente para representar gráficas. Además introduciremos la sintaxis básica para las gráficas en Sage.

Estructuras de Datos Básicas

Lista$\PageIndex{1}$: Data Structures for Graphs

Supongamos que tenemos una gráfica con$n$ vértices que pueden ser indexados por los enteros$1, 2, \dots, n\text{.}$ Aquí hay tres estructuras de datos diferentes que se pueden emplear para representar gráficas.

Matriz de adyacencia: Como vimos en el Capítulo 6, la información sobre los bordes en una gráfica se puede resumir con una matriz de adyacencia,$G\text{,}$ donde$G_{ij}=1$ si y solo si el vértice$i$ está conectado al vértice$j$ en la gráfica. Tenga en cuenta que esto es lo mismo que la matriz de adyacencia para una relación.
Diccionario de bordes: Por cada vértice de nuestra gráfica, mantenemos una lista de aristas que inician en ese vértice. Si$G$ representa la información de borde de la gráfica, entonces denotamos por$G_i$ la lista de vértices que son vértices terminales de aristas iniciando en vértice$i\text{.}$ La sintaxis exacta que se usaría puede variar. Usaremos la sintaxis Sage /Python en nuestros ejemplos.
Edge List: Tenga en cuenta que al crear cualquiera de las dos primeras estructuras de datos, supondríamos que existe una lista de bordes para la gráfica. Una forma sencilla de representar los bordes es mantener esta lista de pares ordenados, o dos conjuntos de elementos, dependiendo de si la gráfica está destinada a ser dirigida o no dirigida. Aquí no trabajaremos con esta estructura de datos, salvo en el primer ejemplo.

Ejemplo$\PageIndex{1}$: A Very Small Example

Consideramos la representación de la siguiente gráfica:

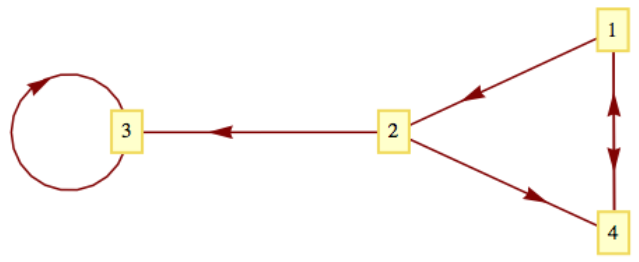$clipboard_e443c66cb08e7538cf6187ed2ba30a9ba.png$ Figura$\PageIndex{1}$: Gráfica para un ejemplo muy pequeño

La matriz de adyacencia que representa la gráfica sería

\ begin {ecuation*} G=\ left (\ begin {array} {cccc} 0 & 1 & 0 & 1\\ 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ end {array}\ right)\ text {.} \ end {ecuación*}

La misma gráfica podría representarse con el diccionario edge

{1: [2,4] ,2: [3,4] ,3: [3] ,4: [1]}.

Observe la forma general de cada ítem en el diccionario: vértice: [lista de vértices].

Por último, una lista de aristas [(1,2), (1,4), (2,3), (2,4), (3,3), (4,1)] también describe la misma gráfica.

Una pregunta natural a hacer es: ¿Qué estructura de datos se debe utilizar en una situación dada? Para las gráficas pequeñas, realmente no hace mucha diferencia. Para matrices más grandes, el recuento de bordes sería una consideración. Si$n$ es grande y el número de bordes es relativamente pequeño, podría usar menos memoria para mantener un diccionario de bordes o una lista de bordes en lugar de construir una$n \times n$ matriz. Algún software para trabajar con gráficas tomará la decisión por ti.

Ejemplo$\PageIndex{2}$: NCAA Basketball

Considera la gráfica del torneo que representa una temporada de básquetbol universitario masculino (o femenino) de la División 1 de la NCAA en Estados Unidos. Hay aproximadamente 350 equipos en la División 1. Supongamos que construimos la gráfica con una arista del equipo A al equipo B si A venció a B al menos una vez en la temporada; y etiquetamos la ventaja con el número de victorias. Dado que el equipo promedio juega alrededor de 30 partidos en una temporada, la mayoría de los cuales serán contra otros equipos de la División I, podríamos esperar alrededor de$\frac{30 \cdot 350}{2}=5,250$ bordes en la gráfica. Esto se vería algo reducido por juegos con equipos de división inferior y casos en los que dos o más victorias sobre el mismo equipo producen una ventaja. Dado que 5,250 es mucho más pequeño que$350^2=122,500$ las entradas en una matriz de adyacencia, un diccionario de bordes o una lista de bordes sería más compacto que una matriz de adyacencia. Incluso si tuviéramos que usar software para crear una matriz de adyacencia, muchos programas identificarán el hecho de que una matriz como la de este ejemplo sería “dispersa” y dejaría los datos en forma de lista y usaría métodos de matriz dispersa para trabajar con ella.

Gráficas

La forma más común de definir una gráfica en Sage es usar un diccionario de borde. Así es como se genera y luego$\PageIndex{1}$ se muestra la gráfica en Ejemplo. Observe que simplemente envolvemos la función DiGraph () alrededor de la misma expresión de diccionario que identificamos anteriormente.

G1 = DiGraph( {1 : [4, 2], 2 : [3, 4], 3 : [3], 4 : [1]})
G1.show()

Puede obtener la matriz de adyacencia de una gráfica con el método adyacency_matrix.

G1.adjacency_matrix()

También se puede definir una gráfica en función de su matriz de adyacencia.

M = Matrix([[0,1,0,0,0],[0,0,1,0,0],[0,0,0,1,0],
              [0,0,0,0,1],[1,0,0,0,0]])
DiGraph(M).show()

La lista de bordes de cualquier gráfico dirigido se puede recuperar fácilmente. Si reemplaza aristas con edge_iterator, puede iterar a través de la lista de bordes. La tercera coordenada de los elementos en el borde es la etiqueta del borde, que es Ninguno en este caso.

DiGraph(M).edges()

Al reemplazar el envoltorio DiGraph () por Graph () se crea una gráfica no dirigida.

G2 = Graph( {1 : [4, 2], 2 : [3, 4], 3 : [3], 4 : [1]})
G2.show()

Hay muchas gráficas especiales y familias de gráficas que están disponibles en Sage a través del módulo de gráficos. Se les hace referencia con los gráficos de prefijo. seguido del nombre y cero o más parámetros entre paréntesis. Aquí hay un par de ellos, primero una gráfica completa con cinco vértices.

graphs.CompleteGraph(5).show()

Aquí hay un gráfico de rueda, llamado así por un patrón obvio de vértices y aristas. Primero le asignamos un nombre y luego mostramos la gráfica sin etiquetar los vértices.

w=graphs.WheelGraph(20)
w.show(vertex_labels=false)

Existen decenas de métodos gráficos, uno de los cuales determina la secuencia de grados de una gráfica. En este caso, es el gráfico de rueda anterior.

w.degree_sequence()

El método de secuencia de grados se define dentro del módulo de grafos, pero los gráficos de prefijo. no es necesario porque el valor de w hereda los métodos de grafos.

Ejercicios

Ejercicio$\PageIndex{1}$

Estimar el número de vértices y aristas en cada una de las siguientes gráficas. ¿Se consideraría escasa la gráfica, de modo que una matriz de adyacencia sería ineficiente?

Vértices: Ciudades del mundo que son atendidas por al menos una aerolínea. Bordes: Pares de ciudades que están conectadas por un vuelo directo regular.
Vértices: caracteres ASCII. Bordes: conecta caracteres que difieren en su código binario en exactamente dos bits.
Vértices: Todas las palabras en inglés. Bordes: Un borde conecta palabra$x$ a palabra$y$ si$x$ es un prefijo de$y\text{.}$

Responder

Una estimación aproximada del número de vértices en la “gráfica aérea mundial” sería el número de ciudades con población mayor o igual a 100 mil. Esto se estima en alrededor de 4,100. Hay muchas ciudades más pequeñas que tienen aeropuertos, pero algunas de las áreas metropolitanas con racimos de grandes ciudades son atendidas por solo unos pocos aeropuertos. 4.000-5.000 probablemente sea una buena suposición. En cuanto a los bordes, eso es un poco más difícil de estimar. Ciertamente no es una gráfica completa. Al observar algunos aeropuertos medianos como Manchester, NH, el número promedio de ciudades a las que puedes ir directamente está en el rango 50-100. Entonces una estimación muy aproximada sería$\frac{75 \cdot 4500}{2}=168,750\text{.}$ Esto es mucho menos que$4,500^2\text{,}$ así una lista de borde o diccionario de algún tipo sería más eficiente.
El número de caracteres ASCII es 128. Cada personaje estaría conectado con$\binom{8}{2}=28$ otros y así hay$\frac{128 \cdot 28}{2}=3,584$ bordes. Comparar esto con el array$128^2=16,384\text{,}$ an es probablemente la mejor opción.
El Oxford English Dictionary como aproximadamente medio millón de palabras, aunque muchas son obsoletas. El número de bordes es probablemente del mismo orden de magnitud que el número de palabras, por lo que una lista de bordes o diccionario es probablemente la mejor opción.

Ejercicio$\PageIndex{2}$

Cada borde de una gráfica está coloreado con uno de los cuatro colores rojo, azul, amarillo o verde. ¿Cómo podría representar los bordes en esta gráfica usando una variación de la estructura de matriz de adyacencia?

Ejercicio$\PageIndex{3}$

Las gráficas dirigidas$G_1, \dots, G_6$, cada una con conjunto de vértices$\{1,2,3,4,5\}$ están representadas por las matrices a continuación. ¿Qué gráficas son isomórficas entre sí?

$G_1: \left( \begin{array}{ccccc} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ \end{array} \right)$$\quad \quad$$G_2: \left( \begin{array}{ccccc} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} \right)$$\quad \quad$$G_3: \left( \begin{array}{ccccc} 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ \end{array} \right)$$G_4: \left( \begin{array}{ccccc} 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} \right)$$\quad \quad$$\quad G_5: \left( \begin{array}{ccccc} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ \end{array} \right)$$\quad \quad$$G_6: \left( \begin{array}{ccccc} 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ \end{array} \right)$

Responder: Cada gráfica es isomórfica consigo misma. Además,$G_2 \text{ and } G_4$ son isomórficos; y$G_3, G_5, \text{ and } G_6$ son isomórficos entre sí.

Ejercicio$\PageIndex{4}$

El siguiente comando Sage verifica que la gráfica de rueda con cuatro vértices es isomórfica a la gráfica completa con cuatro vértices.

graphs.WheelGraph(4).is_isomorphic(graphs.CompleteGraph(4))

Una lista de todas las gráficas en esta base de datos de gráficos está disponible a través de la terminación de pestañas. Escriba “gráficos” y luego haga clic en la tecla de tabulación para ver qué gráficos están disponibles. Esto se puede hacer usando la aplicación Sage o Sage MathCloud, pero no las células de salvia. Encuentra algunos otros pares de gráficas isomórficas en la base de datos.