10.4: Árboles binarios

Última actualización
Guardar como PDF

Page ID: 117151

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Definición de un árbol binario

Un árbol enraizado ordenado es un árbol enraizado cuyos subárboles se ponen en un orden definido y son, ellos mismos, árboles enraizados ordenados. Un árbol vacío y un solo vértice sin descendientes (sin subárboles) son árboles enraizados ordenados.

Ejemplo$\PageIndex{1}$: Distinct Ordered Rooted Trees

Los árboles en Figura$\PageIndex{1}$ son árboles enraizados idénticos, con raíz 1, pero como árboles ordenados, son diferentes.

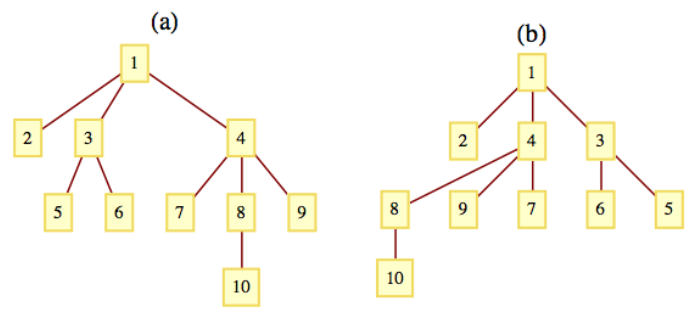$clipboard_e20c96fad3a2d8bd0a740e2b30161f39d.png$ Figura$\PageIndex{1}$: Dos árboles enraizados ordenados diferentes

Si un árbol enraizado$v$ tiene$p$ subárboles, nos referiríamos a ellos como los primero, segundo,...,$p^{th}$ subárboles. Hay una sutil diferencia entre ciertos árboles ordenados y árboles binarios, que definimos a continuación.

Definición$\PageIndex{1}$: Binary Tree

Un árbol que no consta de vértices (el árbol vacío) es un árbol binario
Un vértice junto con dos subárboles que son ambos árboles binarios es un árbol binario. Los subárboles se llaman los subárboles izquierdo y derecho del árbol binario.

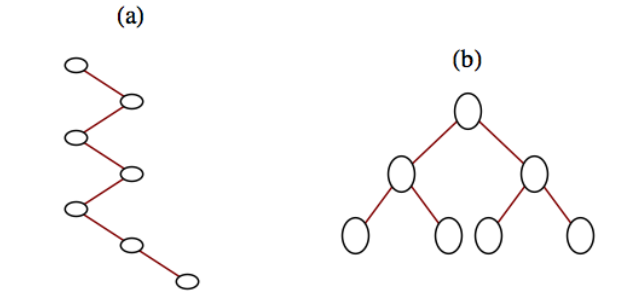
La diferencia entre árboles binarios y árboles ordenados es que cada vértice de un árbol binario tiene exactamente dos subárboles (uno o ambos pueden estar vacíos), mientras que un vértice de un árbol ordenado puede tener cualquier número de subárboles. Pero hay otra diferencia significativa entre los dos tipos de estructuras. Los dos árboles de la Figura$\PageIndex{2}$ serían considerados idénticos a los árboles ordenados. Sin embargo, son diferentes árboles binarios. El árbol (a) tiene un subárbol derecho vacío y el árbol (b) tiene un subárbol izquierdo vacío.

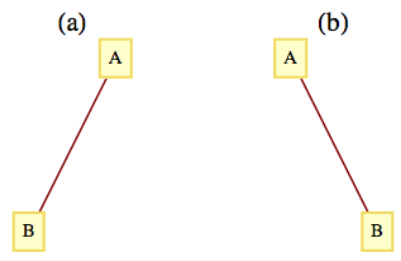$clipboard_ef19a1d98877a4631a131310b14685f3b.png$ Figura$\PageIndex{2}$: Dos árboles binarios diferentes

Lista$\PageIndex{1}$: Terminology and General Facts about Binary Trees

Un vértice de un árbol binario con dos subárboles vacíos se llama hoja. Todos los demás vértices se denominan vértices internos.
El número de hojas en un árbol binario puede variar desde una hasta aproximadamente la mitad del número de vértices en el árbol (ver Ejercicio$\PageIndex{4}$ de esta sección).
El número máximo de vértices a nivel$k$ de un árbol binario es$2^k$,$k\geq 0$ (ver Ejercicio$\PageIndex{6}$ de esta sección).
Un árbol binario completo es un árbol para el cual cada vértice tiene cero o dos subárboles vacíos. Es decir, cada vértice tiene dos o cero hijos. Consulte Ejercicio$\PageIndex{7}$ de esta sección para un dato general sobre los árboles binarios completos.

Traversos de árboles binarios

El recorrido de un árbol binario consiste en visitar cada vértice del árbol en algún orden prescrito. A diferencia de los recorridos gráficos, los vértices consecutivos que se visitan no siempre están conectados con un borde. Los recorridos de árboles binarios más comunes se diferencian por el orden en que se visita la raíz y sus subárboles. Los tres travesales se describen mejor de forma recursiva y son:

Definición$\PageIndex{2}$: Preorder Traversal

Visita la raíz del árbol.
Preorder atravesar el subárbol izquierdo.
Preorder atravesar el subárbol derecho.

Definición$\PageIndex{3}$: Inorder Traversal

En orden atraviese el subárbol izquierdo.
Visita la raíz del árbol.
En orden atraviese el subárbol derecho.

Definición$\PageIndex{4}$: Postorder Traversal

Postorder atravesar el subárbol izquierdo.
Postorder atraviesa el subárbol derecho.
Visita la raíz del árbol.

Cualquier recorrido de un árbol vacío consiste en no hacer nada.

Ejemplo$\PageIndex{2}$: Traversal Examples

Para el árbol de la Figura$\PageIndex{3}$, los órdenes en los que se visitan los vértices son:

A-B-D-E-C-F-G, para el recorrido de preorden.
D-B-E-A-F-C-G, para el recorrido en orden.
D-E-B-F-G-C-A, para el recorrido postorder.

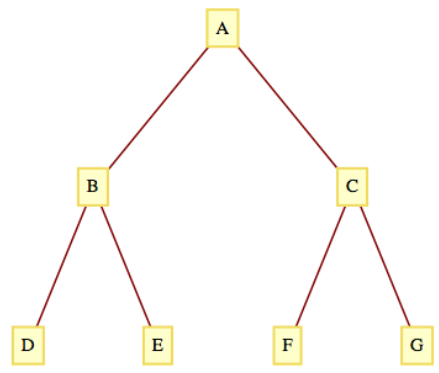$clipboard_ebd0f8ef2775aa6c8a4d40c91a450c3ff.png$ Figura$\PageIndex{3}$: Un árbol binario completo hasta el nivel 2

Ordenación de árbol binario. Dada una colección de enteros (u otros objetos que se pueden ordenar), una técnica para ordenar es una ordenación de árbol binario. Si los enteros son$a_1\text{,}$$a_2, \ldots \text{,}$$a_n\text{,}$$n\geq 1\text{,}$ ejecutamos primero el siguiente algoritmo que crea un árbol binario:

Algorithm$\PageIndex{1}$: Binary Sort Tree Creation

Insertar$a_1$ en la raíz del árbol.
Para k: = 2 a n//$a_k$insertar en el árbol
1. r =$a_1$
2. insertado = falso
3. while not (insertado):
  $\quad $ si$a_k < r\text{:}$
  $\quad \quad \quad $ si$r$ tiene un hijo izquierdo:
  $\quad \quad \quad \quad$ r = left child of$r$
  $\quad \quad \quad$ else:
  $\quad \quad \quad \quad$ make$a_k$ the left child de$r$
  $\quad \quad \quad \quad$ insertado = true
  $\quad \quad$ else:
  $\quad \quad \quad $ si$r$ tiene un hijo derecho:
  $\quad \quad \quad \quad$ r = hijo derecho de$r$
  $\quad \quad \quad$ else:
  $\quad \quad \quad \quad$hacer que$a_k$ el hijo correcto de$r$
  $\quad \quad \quad \quad$ insertado = verdadero

Si los enteros a ordenar son 25, 17, 9, 20, 33, 13 y 30, entonces el árbol que se crea es el de la Figura$\PageIndex{4}$. El recorrido en orden de este árbol es 9, 13, 17, 20, 25, 30, 33, los enteros en orden ascendente. En general, el recorrido en orden del árbol que se construye en el algoritmo anterior producirá una lista ordenada. Los cruces de preorden y postorden del árbol no tienen sentido aquí.

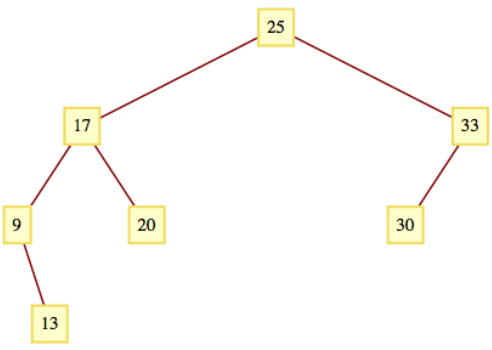$clipboard_ea8e7b78f73cedcafa4a485d15eae9f28.png$ Figura$\PageIndex{4}$: Un árbol de clasificación binaria

Árboles de Expresión

Una forma conveniente de visualizar una expresión algebraica es mediante su árbol de expresión. Considera la expresión

\ comenzar {ecuación*} X = a*b - c/d + e.\ fin {ecuación*}

Dado que es costumbre poner precedencia sobre multiplicación/divisiones,$X$ se evalúa como multiplicación/divisiones$((a*b) -(c/d)) + e\text{.}$ consecutivas o sumas/restas se evalúan de izquierda a derecha. Podemos analizar$X$ más a fondo señalando que es la suma de dos expresiones más simples$(a*b) - (c/d)$ y$e\text{.}$ La primera de estas expresiones se puede desglosar aún más en la diferencia de las expresiones$a*b$ y$c/d\text{.}$ Cuando descomponemos cualquier expresión en$(\textrm{left expression})\textrm{operation} (\textrm{right expression})\text{,}$ el árbol de expresiones de esa expresión es el árbol binario cuya raíz contiene la operación y cuyos subárboles izquierdo y derecho son los árboles de las expresiones izquierda y derecha, respectivamente. Adicionalmente, una variable simple o un número tiene un árbol de expresiones que es un solo vértice que contiene la variable o número. La evolución del árbol de expresión para expresión$X$ aparece en la Figura$\PageIndex{5}$.

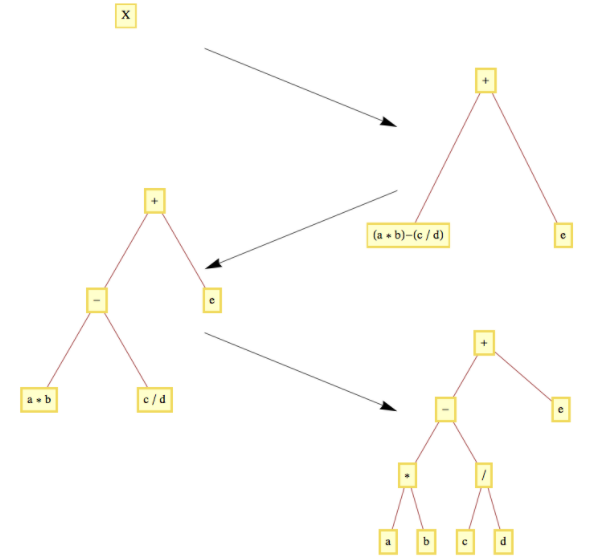$clipboard_e762973865cfaa47958794d3b6419f5a5.png$ Figura$\PageIndex{5}$: Construyendo un árbol de expresión

Ejemplo$\PageIndex{3}$: Some Expression Trees

Si pretendemos aplicar las operaciones de suma y resta en$X$ primer lugar, pondríamos entre paréntesis la expresión a$a*(b - c)/(d + e)\text{.}$ Su árbol de expresión aparece en la Figura$\PageIndex{6}$ (a).
Los árboles de expresión para$a^2-b^2$ y para$(a + b)*(a - b)$ aparecen en la Figura$\PageIndex{6}$ (b) y Figura$\PageIndex{6}$ (c).

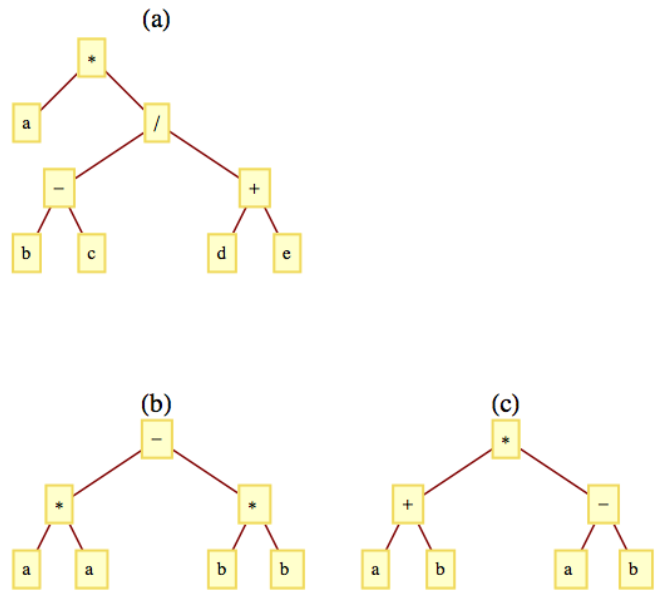$clipboard_ea66227964d09c2db7c5a5ab97b4e2881.png$ Figura$\PageIndex{6}$: Ejemplos de árboles de expresión

Los tres cruces de un árbol de operaciones son todos significativos. Una operación binaria aplicada a un par de números se puede escribir de tres maneras. Una es la forma de infijo familiar, como$a + b$ para la suma de$a$ y$b\text{.}$ Otra forma es prefijo, en la que se escribe la misma suma$+a b\text{.}$ La forma final es postfix, en la que se escribe la suma Expresiones$a b+\text{.}$ algebraicas que involucran las cuatro operaciones aritméticas estándar$(+,-,*, \text{and} /)$ en forma de prefijo y postfijo se definen de la siguiente manera:

Lista$\PageIndex{2}$: Prefix and Postfix Forms of an Algebraic Expression

Prefijo

Una variable o número es una expresión de prefijo
Cualquier operación seguida de un par de expresiones de prefijo es una expresión de prefijo.

Postfix

Una variable o número es una expresión de postfijo
Cualquier par de expresiones de postfix seguido de una operación es una expresión de postfix.

La conexión entre los recorridos de un árbol de expresión y estas formas es simple:

El recorrido de preorden de un árbol de expresión dará como resultado la forma de prefijo de la expresión.
El recorrido postorder de un árbol de expresión dará como resultado la forma postfix de la expresión.
El recorrido en orden de un árbol de operaciones no producirá, en general, la forma apropiada de infijo de la expresión. Si una expresión requiere paréntesis en forma de infijo, un recorrido en orden de su árbol de expresión tiene el efecto de eliminar los paréntesis.

Ejemplo$\PageIndex{4}$: Traversing an Expression Tree

El recorrido de preorden del árbol en la Figura$\PageIndex{5}$ es$+-*ab/cd e\text{,}$ cuál es la versión de prefijo de$X\text{.}$ la expresión El recorrido postorden es$ab*cd/-e+\text{.}$ Tenga en cuenta que dado que la forma original de no$X$ necesitaba paréntesis, el recorrido en orden,$a*b-c/d+e\text{,}$ es la versión correcta del infijo.

Contar árboles binarios

Cerramos esta sección con una fórmula para el número de diferentes árboles binarios con$n$ vértices. La fórmula se deriva usando funciones generadoras. Si bien los detalles completos están fuera del alcance de este texto, ofreceremos una visión general de la derivación para ilustrar cómo se utilizan las funciones generadoras en la combinatoria avanzada.

Dejar$B(n)$ ser el número de diferentes árboles binarios de tamaño$n$ ($n$vértices),$n \geq 0\text{.}$ Por nuestra definición de un árbol binario,$B(0) = 1\text{.}$ Ahora considere cualquier entero positivo$n + 1\text{,}$$n \geq 0\text{.}$ Un árbol binario de tamaño$n + 1$ tiene dos subárboles, los tamaños de los cuales se suman a$n\text{.}$ La las posibilidades se pueden dividir en$n + 1$ casos:

Caso 0: El subárbol izquierdo tiene tamaño 0; el subárbol derecho tiene tamaño$n\text{.}$

Caso 1: El subárbol izquierdo tiene tamaño 1; el subárbol derecho tiene tamaño$n - 1\text{.}$

$\quad \quad $$\vdots$

Caso El subárbol$k\text{:}$ izquierdo tiene tamaño subárbol$k\text{;}$ derecho tiene tamaño$n - k\text{.}$

$\quad \quad $$\vdots$

Caso$n\text{:}$ Izquierdo subárbol tiene tamaño subárbol$n\text{;}$ derecho tiene tamaño 0.

En el Caso general$k\text{,}$ podemos contar el número de posibilidades multiplicando el número de formas en que se puede llenar el subárbol izquierdo,$B(k)\text{,}$ por el número de formas en que se puede llenar el subárbol derecho. $B(n-k)\text{.}$Dado que la suma de estos productos es igual,$B(n + 1)\text{,}$ obtenemos la relación de recurrencia para$n\geq 0\text{:}$

\ begin {equation*}\ begin {split} B (n+1) &= B (0) B (n) + B (1) B (n-1) +\ cdots + B (n) B (0)\\ &=\ sum_ {k=0} ^n B (k) B (n-k)\ end {split}\ end {equation*}

Ahora toma la función generadora de ambos lados de esta relación de recurrencia:

\[\label{eq:1}\sum\limits_{n=0}^\infty B(n+1)z^n=\sum\limits_{n=0}^\infty\left(\sum\limits_{k=0}^n B(k)B(n-k)\right)z^n\]

\[\label{eq:2} G(B\uparrow ;z)=G(B*B;z)=G(B;z)^2\]

Recordemos que$G(B\uparrow;z) =\frac{G(B;z)-B(0)}{z}=\frac{G(B;z)-1}{z}$ si$G\text{,}$ abreviamos$G(B; z)$ a obtenemos

\ begin {ecuación*}\ frac {G-1} {z} = G^2\ Rightarrow z G^2- G + 1 = 0\ end {ecuación*}

Usando la ecuación cuadrática encontramos dos soluciones:

\[\begin{align}\label{eq:3}G_1 &=\frac{1+\sqrt{1-4z}}{2z}\text{ and} \\ \label{eq:4}G_2&=\frac{1-\sqrt{1-4z}}{2z}\end{align}\]

La brecha en nuestra derivación ocurre aquí ya que no presumimos un conocimiento de cálculo. Si nos expandimos$G_1$ como una serie de potencia extendida, encontramos

\[\label{eq:5}G_1=\frac{1+\sqrt{1-4z}}{2z}=\frac{1}{z}-1-z-2z^2-5z^3-14z^4-42z^5+\cdots\]

Los coeficientes después del primero son todos negativos y hay una singularidad a 0 por el$\frac{1}{z}$ término. Sin embargo si hacemos lo mismo con$G_2$ obtenemos

\[\label{eq:6}G_2=\frac{1-\sqrt{1-4z}}{2z}=1+z+2z^2+5z^3+14z^4+42z^5+\cdots\]

Un análisis posterior conduce a una expresión de forma cerrada para la$B(n)\text{,}$ cual es

\ begin {ecuación*} B (n) =\ frac {1} {n+1}\ left (\ begin {array} {c} 2n\\ n\\ end {array}\ derecha)\ end {ecuación*}

Esta secuencia de números se suele llamar los números catalanes. Para obtener más información sobre los números catalanes, consulte la entrada A000108 en La Enciclopedia On-Line de Secuencias Entero.

Nota Sage Math - Serie Power

Puede ser interesante observar cómo las expansiones de la serie de potencia extendida de$G_1$ y$G_2$ se determinan usando Sage. En Sage, uno tiene la capacidad de ser muy específico sobre cómo deben interpretarse las expresiones algebraicas especificando el anillo subyacente. Esto puede hacer que trabajar con varias expresiones algebraicas sea un poco más confuso para el principiante. Aquí te explicamos cómo conseguir una expansión Laurent para$G_1$ arriba.

R.<z>=PowerSeriesRing(ZZ,'z')
G1=(1+sqrt(1-4*z))/(2*z)
G1

La primera expresión de Sage anterior declara una estructura llamada anillo que contiene series de poder. No estamos usando toda esa estructura, solo un elemento específico, G1. Entonces, lo importante de esta primera entrada es que establece z como una variable asociada con series de potencia sobre los enteros. Cuando la segunda expresión define el valor de G1 en términos de z, se convierte automáticamente en una serie de potencia.

La expansión de$G_2$ usa código idéntico, y sus coeficientes son los valores de$B(n)\text{.}$

En el Capítulo 16 presentaremos anillos y podremos aprovechar aún más las capacidades de Sage en esta área.

Ejercicios

Ejercicio$\PageIndex{1}$

Dibuje los árboles de expresión para las siguientes expresiones:

$\displaystyle a(b + c)$
$\displaystyle a b + c$
$\displaystyle a b + a c$
$\displaystyle b b - 4 a c$
$\displaystyle \left(\left(a_3 x + a_2\right)x +a_1\right)x + a_0$

Contestar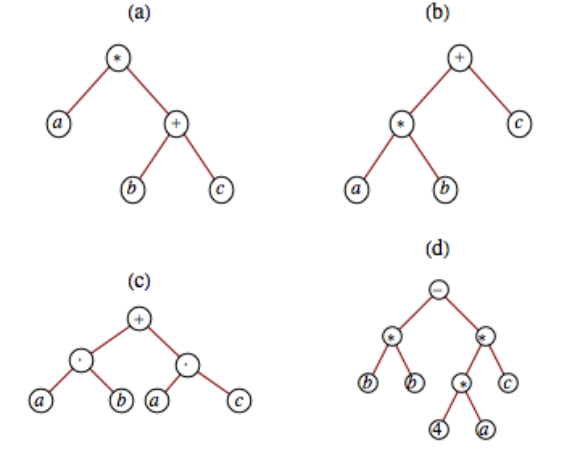: $clipboard_e3fc5c9467732da1e444d485faa1a3334.png$ Figura$\PageIndex{7}$

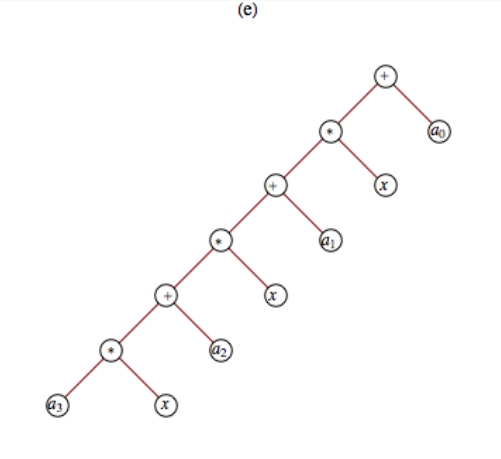$clipboard_eed8118102b8b48e4af211060fefb0703.png$ Figura$\PageIndex{8}$

Ejercicio$\PageIndex{2}$

Dibuja los árboles de expresión para

$\displaystyle \frac{x^2-1}{x-1}$
$\displaystyle x y + x z + y z$

Ejercicio$\PageIndex{3}$

Escriba los recorridos de preorden, inorden y postorden de los árboles en el Ejercicio$\PageIndex{1}$ anterior.

Contestar: \ begin {ecuation*}\ begin {array} {cccc} &\ text {Preorder} &\ text {En orden} &\ text {Postorder}\\ (a) &\ cdot a + b c & a\ cdot b+c & a b c +\ cdot\ (b) & +\ cdot a b c & a\ cdot cdot +\\ (c) & +\ cdot a b\ cdot a c & a\ cdot b+a\ cdot c & a b\ cdot a c\ cdot +\\ \ end {array}\ end {ecuación*}

Ejercicio$\PageIndex{4}$

Verifique la fórmula para$B(n)\text{,}$$0 \leq n \leq 3$ dibujando todos los árboles binarios con tres o menos vértices.

Ejercicio$\PageIndex{5}$

Dibuja un árbol binario con siete vértices y una sola hoja.
Dibuja un árbol binario con siete vértices y tantas hojas como sea posible.

Contestar: Agrega textos aquí. No borre primero este texto.

$clipboard_e07d9d21c4bd5ac54a0e80839263e1bcc.png$ Figura$\PageIndex{9}$

Ejercicio$\PageIndex{6}$

Demostrar que el número máximo de vértices a nivel$k$ de un árbol binario es$2^k$ y que un árbol con tantos vértices a nivel$k$ debe tener$2^{k+1}-1$ vértices.

Ejercicio$\PageIndex{7}$

Demostrar que si$T$ es un árbol binario completo, entonces el número de hojas de$T$ es uno más que el número de vértices internos (no-hojas).

Contestar

Solución 1:

Base: Un árbol binario que consiste en un solo vértice, que es una hoja, satisface la ecuación$\text{leaves }=\text{ internal vertices }+1$

Inducción: Supongamos que para algunos$k\geq 1$, todos los árboles binarios completos con$k$ o menos vértices tienen una hoja más que los vértices internos. Ahora considere cualquier árbol binario completo con$k+1$ vértices. Dejar$T_{A}$ y$T_{B}$ ser los subárboles izquierdo y derecho del árbol que, por la definición de un árbol binario completo, deben estar ambos llenos. Si$i_{A}$ y$i_{B}$ son los números de vértices internos en$T_{A}$ y$T_{B}$, y$j_{A}$ y$j_{B}$ son los números de hojas, entonces$j_{A}=i_{A}+1$ y$j_{B}=i_{B}+1$. Por lo tanto, en todo el árbol,

\[\begin{aligned}\text{the number of leaves }&=j_{A}+j_{B} \\ &=(i_{A}+1)+(i_{B}+1) \\ &=(i_{A}+i_{B}+1)+1 \\ &=(\text{number of internal vertices})+1\end{aligned}\]

Solución 2:

Imagínese construir un árbol binario completo comenzando con un solo vértice. Al continuar agregando hojas en pares para que el árbol permanezca lleno, podemos construir cualquier árbol binario completo. Nuestro árbol inicial satisface la condición de que el número de hojas sea una más que el número de vértices internos. Al agregar un par de hojas a un árbol binario completo, una hoja vieja se convierte en un vértice interno, aumentando el número de vértices internos en uno. Aunque perdemos una hoja, las dos hojas agregadas crean un aumento neto de una hoja. Por lo tanto, se mantiene la igualdad deseada.