13.2: Celosías

Última actualización
Guardar como PDF

Page ID: 117196

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección, restringimos nuestra discusión a las celosías, aquellos posets para los que cada par de elementos tiene tanto un límite inferior mayor como un límite menor superior. Primero introducimos alguna notación.

Definición $\PageIndex{1}$: Join, Meet

Dejemos$(L, \preceq)$ ser un poset, y$a, b \in L\text{.}$ definimos:

$a \lor b\text{,}$leer “$a$unirse$b$”, como el límite inferior superior de$a$ y$b\text{,}$ si existe. y
$a \land b\text{,}$leer “$a$cumplir$b$”, como el mayor límite inferior de$a$ y$b\text{,}$ si existe.

Dado que los unir y conocer producen un resultado único en todos los casos en que existan, por el Teorema 13.1.1, podemos considerarlos como operaciones binarias en un conjunto si siempre existen. Así, la siguiente definición:

Definición $\PageIndex{2}$: Lattice

Una celosía es un poset$(L, \preceq)$ para el cual cada par de elementos tiene un límite inferior mayor y un límite menor superior. Ya que una celosía$L$ es un sistema algebraico con operaciones binarias$\lor$ y$\land\text{,}$ se denota por$[L; \lor, \land]\text{.}$ Si queremos dejar claro en qué se basa el ordenamiento parcial del enrejado, decimos que es una celosía bajo$\preceq\text{.}$

Ejemplo$\PageIndex{1}$: The Power Set of a Three Element Set

Consideremos el poset$(\mathcal{P}(A),\subseteq)$ que examinamos en el Ejemplo 13.1.3. No es demasiado sorprendente que cada par de conjuntos tuviera un mayor límite inferior y menor límite superior. Así, tenemos una celosía en este caso; y$A\lor B = A \cup B$ y Se anima$A\land B = A \cap B\text{.}$ al lector a escribir las mesas de operaciones$[\mathcal{P}(A); \cup, \cap]\text{.}$

Nuestra primera celosía de hormigón puede generalizarse al caso de cualquier conjunto que$A\text{,}$ produzca la celosía$[\mathcal{P}(A); \lor, \land]\text{,}$ donde la operación de unión es la operación de conjunto de unión y la operación de encuentro es la intersección de operación; es decir,$\lor =\cup$ y$\land =\cap\text{.}$

Se puede demostrar (ver los ejercicios) que las leyes conmutativas, las leyes asociativas, las leyes idempotentes y las leyes de absorción son todas ciertas para cualquier celosía. Un ejemplo concreto de ello es claramente$[\mathcal{P}(A); \cup, \cap ]\text{,}$ ya que estas leyes se mantienen en el álgebra de conjuntos. Esta celosía también tiene propiedad distributiva en que la unión es distributiva sobre la reunión y la reunión es distributiva sobre la unión. Sin embargo, este no es siempre el caso de las celosías en general.

Definición$\PageIndex{3}$: Distributive Lattice

Dejar$\mathcal{L}=[L; \lor, \land ]$ ser una celosía debajo$\preceq$. $\mathcal{L}$se llama celosía distributiva si y sólo si las leyes distributivas se mantienen; es decir, por todo$a, b, c \in L$ lo que tenemos

\ begin {ecuación*}\ begin {array} {c} a\ lor (b\ land c) = (a\ lor b)\ land (a\ lor c)\\ y\\ a\ land (b\ lor c) = (a\ land b)\ lor (a\ land c)\\ end {array}\ end {array}\ end {ecuación*}

Ejemplo $\PageIndex{2}$: A Nondistributive Lattice

Damos ahora un ejemplo de una celosía donde las leyes distributivas no se sostienen. Dejar$L = \{\pmb{0},a,b,c,\pmb{1}\}\text{.}$ Definimos el orden parcial$\preceq$ encendido$L$ por el conjunto

\ begin {ecuación*}\ {(\ pmb {0},\ pmb {0}), (\ pmb {0}, a), (\ pmb {0}, b), (\ pmb {0}, c), (\ pmb {0},\ pmb {1}), (a, a), (a,\ pmb {1}), (b, b), (b,\ pmb {1}), (c, c), (c,\ pmb {1}), (\ pmb {1},\ pmb {1})\}\ final {ecuación*}

Las mesas de operaciones para$\lor$ y$\land$ sobre$L$ son:

\ begin {ecuación*}\ begin {array} {cc}\ begin {array} {c|ccccc}\ lor &\ pmb {0} & a & b & c &\ pmb {1}\\ hline\ pmb {0} &\ pmb {0} & a & b & c &\ pmb {1}\ pmb {1}\\ a & a & a &\ pmb {1} &\ pmb {1} &\ pmb {1}\\ b & b &\ pmb {1} & b &\ pmb {1} &\ pmb {1}\\ c & c &\ pmb {1} &\ pmb {1} & c &\ pmb {1}\\ pmb {1} &\ pmb {1} &\ pmb {1} &\ pmb {1} &\ pmb {1} &\ pmb {1} &\ pmb {1}\\ end {array} &\ begin {array} {c|ccccc}\ tierra y\ pmb {0} & a & b & c &\ pmb {1}\\\ hline\ pmb {0} &\ pmb {0} &\ pmb {0} &\ pmb {0} &\ pmb { 0} &\ pmb {0}\\ a &\ pmb {0} & a &\ pmb {0} &\ pmb {0} &\ pmb {0} &\ pmb {0} &\ pmb {0} &\ pmb {0} & b\\ c &\ pmb {0} &\ pmb {0} &\ pmb {0} &\ pmb {0} & c & c\\\ pmb {1} &\ pmb {0} & a & b & c &\ pmb {1}\\\ end {array}\\ end {array}\ end {array}\ end {ecuación*}

Dado que cada par de elementos en$L$ tiene tanto una unión como una reunión,$[L; \lor , \land ]$ es una celosía (bajo divisiones). ¿Esta celosía es distributiva? Observamos que:$a \lor (c \land b) = a \lor \pmb{0} = a$ y$(a \lor c) \land (a \lor b) = \pmb{1} \land \pmb{1} = \pmb{1}\text{.}$ Por lo tanto,$a \lor (b \land c) \neq (a \lor b) \land (a \lor c)$ para algunos valores de$a, b, c \in L\text{.}$ Así, esta celosía no es distributiva.

Nuestra siguiente observación utiliza el término “sublattice”, que no hemos definido en este momento, pero esperaríamos que se pudiera anticipar una definición, y la dejaremos como ejercicios para hacerlo.

Se puede demostrar que una celosía es no distributiva si y sólo si contiene un sublattice isomórfico a una de las celosías de la Figura$\PageIndex{1}$. El diagrama de orden a la derecha de esta figura, produce la celosía de diamante, que es precisamente la que se define en Ejemplo$\PageIndex{2}$. La celosía basada en el poset de la izquierda se llama celosía del pentágono.

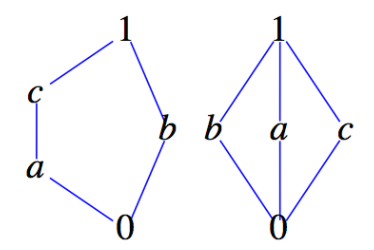$clipboard_ed6294eb14e1c07499d036e6ed2294341.png$ Figura$\PageIndex{1}$: Celosías no distributivas, las celosías de pentágono y diamante

13.2.1: Ejercicios

Ejercicio$\PageIndex{1}$

$L$Sea el conjunto de todas las proposiciones generadas por$p$ y$q\text{.}$ ¿Cuáles son las operaciones de encuentro y unión en esta celosía bajo implicación? ¿Cuáles son los elementos máximos y mínimos?

Ejercicio$\PageIndex{2}$

¿Cuáles de los posets en el Ejercicio 13.1.3 son celosías? ¿Cuáles de las celosías son distributivas?

Ejercicio$\PageIndex{3}$

Declarar las leyes conmutativas, las leyes asociativas, las leyes idempotentes y las leyes de absorción para celosías.
Demuestre las leyes que declaró.

Ejercicio$\PageIndex{4}$

Demostrar que la celosía del pentágono es no distributiva.

Ejercicio$\PageIndex{5}$

¿Cuál es una definición razonable del término sublattice?

Contestar: Una definición razonable sería esta: Dejar$[L; \lor, \land ]$ ser una celosía y dejar$K$ ser un subconjunto no vacío de$L\text{.}$ Entonces$K$ es un sublattice de$L$ si y solo si$K$ se cierra bajo ambos$\lor$ y$\land$

Ejercicio$\PageIndex{6}$

Dejar$[L; \lor , \land ]$ ser una celosía basada en un ordenamiento parcial$\preceq\text{.}$ Demostrar que si$a, b, c \in L\text{,}$

$a \preceq a \lor b \text{.}$
$a \land b \preceq a\text{.}$
$b \preceq a$y$c \preceq a \Rightarrow b \lor c \preceq a\text{.}$