13.1: Posets revisitados

Recordamos la definición de un orden parcial:

Definición\(\PageIndex{1}\): Partial Ordering

\(\preceq\)Sea una relación sobre un conjunto\(L\text{.}\) Decimos que\(\preceq\) es un ordenamiento parcial sobre\(L\) si es reflexivo, antisimétrico, y transitivo. Es decir:

1. \(\preceq\)es reflexivo:\(a \preceq a \quad \forall a \in L\)
2. \(\preceq\)es antisimétrico:\(a \preceq b \textrm{ and } a \neq b \Rightarrow b \npreceq a \quad \forall a,b \in L\)
3. \(\preceq\)es transitivo:\(a \preceq b \textrm{ and } b \preceq c \Rightarrow a \preceq c \quad \forall a,b,c \in L\)

El conjunto junto con la relación\((L, \preceq)\) se llama poset.

Ejemplo\(\PageIndex{1}\): Some Posets

Recordamos algunos ejemplos de posets:

1. \((\mathbb{R}, \leq)\)es un poset. Observe que nuestro símbolo genérico para el ordenamiento parcial,\(\preceq\text{,}\) se selecciona para recordarnos que un orden parcial es similar a “menor o igual a”.
2. Let\(A=\{a,b\}\text{.}\) Entonces\((\mathcal{P}(A) ,\subseteq)\) es un poset.
3. Let\(L = \{1, 2, 3, 6\}\text{.}\) Entonces\((L,\mid)\) es un poset.

Los posets en los que nos concentraremos en este capítulo serán aquellos que tengan límites superior e inferior en relación con cualquier par de elementos. A continuación, definimos este concepto con precisión.

Definición\(\PageIndex{2}\): Lower Bound, Upper Bound

Dejar\((L, \preceq)\) ser un poset, y\(a, b \in L\text{.}\) Entonces\(c \in L\) es un límite inferior de\(a\) y\(b\) si\(c \preceq a\) y\(c \preceq b\text{.}\) También,\(d \in L\) es un límite superior de\(a\) y\(b\) si\(a \preceq d\) y\(b \preceq d\text{.}\)

En la mayoría de los posets que nos interesarán, cada par de elementos tiene límites tanto superior como inferior, aunque hay posets para los que esto no es cierto.

Definición\(\PageIndex{3}\): Greatest Lower Bound

\((L, \preceq)\)Déjese ser un poset. Si\(a, b \in L\text{,}\) entonces\(\ell \in L\) es un mayor límite inferior de\(a\) y\(b\) si y solo si

• \(\displaystyle \ell \preceq a\)
• \(\displaystyle \ell \preceq b\)
• Si\(\ell' \in L\) tal que\(\ell' \preceq a\) y\(\ell' \preceq b\text{,}\) luego\(\ell' \preceq \ell\text{.}\)

La última condición en la definición de LímiteInferior Mayor dice que si también\(\ell'\) es un límite inferior, entonces\(\ell\) es “mayor” en relación a\(\preceq\) que\(\ell'\text{.}\) La definición de un límite inferior mínimo es una imagen especular de un límite inferior mayor:

Definición\(\PageIndex{4}\): Least Upper Bound

\((L, \preceq)\)Déjese ser un poset. Si\(a, b \in L\text{,}\) entonces\(u \in L\) es un límite superior mínimo de\(a\) y\(b\) si y solo si

• \(\displaystyle a \preceq u\)
• \(\displaystyle b \preceq u\)
• Si\(u' \in L\) tal que si\(a \preceq u'\) y\(b \preceq u'\text{,}\) entonces\(u \preceq u'\text{.}\)

Observe que las dos definiciones anteriores se refieren a “... un límite inferior mayor” y “un límite mínimo superior”. Cada vez que definas un objeto como estos necesitas tener una mente abierta en cuanto a si puede existir más de uno de esos objetos. De hecho, ahora podemos demostrar que no puede haber dos mayores límites inferiores o dos menos límites superiores.

Teorema \(\PageIndex{1}\): Uniqueness of Least Upper and Greatest Lower Bounds

Dejar\((L, \preceq)\) ser un poset, y\(a, b \in L\text{.}\) Si un mayor límite inferior de\(a\) y\(b\) existe, entonces es único. Lo mismo ocurre con un límite mínimo superior, si existe.

Prueba

Dejar\(\ell\) y\(\ell'\) ser mayores límites inferiores de\(a\) y\(b\text{.}\) Vamos a demostrar que\(\ell=\ell'\text{.}\)

1. \(\ell\)un límite inferior mayor de\(a\) y\(b\)\(\Rightarrow\)\(\ell\) es un límite inferior de\(a\) y\(b\text{.}\)
2. \(\ell'\)un límite inferior mayor de\(a\) y\(b\) y\(\ell\) un límite inferior de\(a\) y\(b\)\(\Rightarrow \ell \preceq \ell'\text{,}\) por la definición de mayor límite inferior.
3. \(\ell'\)un límite inferior mayor de\(a\) y\(b\)\(\Rightarrow \ell'\) es un límite inferior de\(a\) y\(b\text{.}\)
4. \(\ell\)un límite inferior mayor de\(a\) y\(b\) y\(\ell'\) un límite inferior de\(a\) y\(b\text{.}\)\(\Rightarrow \ell' \preceq \ell\) por la definición de mayor límite inferior.
5. \(\ell\preceq \ell'\)y\(\ell'\preceq \ell \Rightarrow \ell=\ell'\) por la propiedad antisimetría de un ordenamiento parcial.

La prueba de la segunda afirmación en el teorema es casi idéntica a la primera y se deja al lector.

Definición \(\PageIndex{5}\): Greatest Element, Least Element

\((L, \preceq)\)Déjese ser un poset. \(M \in L\)se llama el elemento mayor (máximo) de\(L\) si, para todos\(a \in L\text{,}\)\(a \preceq M\text{.}\) Además,\(m \in L\) se llama el elemento menor (mínimo) de\(L\) si para todos\(a \in L\text{,}\)\(m \preceq a\text{.}\) Los elementos mayores y menores, cuando existen, se denotan frecuentemente por\(\pmb{1}\) y \(\pmb{0}\)respectivamente.

Ejemplo\(\PageIndex{2}\): Bounds on the Divisors of 105

Considera el orden parcial “divide” en\(L = \{1, 3, 5, 7, 15, 21, 35, 105\}\text{.}\) Entonces\((L, \mid)\) es un poset. Para determinar el límite inferior superior de 3 y 7, buscamos todos\(u \in L\text{,}\) tales que\(3|u\) y\(7|u\text{.}\) Ciertamente, ambos\(u = 21\) y\(u = 105\) satisfacer estas condiciones y ningún otro elemento de\(L\) hace. A continuación, ya que\(21|105\text{,}\)\(21\) es el límite inferior superior de 3 y 7. De igual manera, el límite inferior superior de 3 y 5 es 15. El mayor elemento de\(L\) es 105 ya que\(a|105\) para todos\(a \in L\text{.}\) Para encontrar el mayor límite inferior de 15 y 35, primero consideramos todos los elementos\(g\) de\(L\) tal que\(g \mid 15\text{.}\) sean 1, 3, 5, y 15. Los elementos para los cuales\(g \mid 35\) son 1, 5, 7 y 35. A partir de estas dos listas, vemos eso\(\ell = 5\) y\(\ell = 1\) satisfacemos las condiciones requeridas. Pero como\(1|5\text{,}\) el mayor límite inferior es el 5. El elemento mínimo de\(L\) es 1 ya que\(1|a\) para todos\(a \in L\text{.}\)

Definición \(\PageIndex{6}\): The Set of Divisors of an Integer

Para cualquier entero positivo\(n\text{,}\) los divisores de\(n\) es el conjunto de enteros que se dividen uniformemente en\(n\text{.}\) Denotamos este conjunto\(D_n\text{.}\)

Por ejemplo, el conjunto\(L\) de Ejemplo\(\PageIndex{2}\) es\(D_{105}\text{.}\)

Ejemplo \(\PageIndex{3}\): The Power Set of a Three Element Set

Considera el poset\((\mathcal{P}(A),\subseteq)\text{,}\) donde\(A = \{1, 2, 3\}\text{.}\) El mayor límite inferior de\(\{1, 2\}\) y\(\{1,3\}\) es\(\ell = \{1\}\text{.}\) Para cualquier otro elemento\(\ell'\) que sea un subconjunto de\(\{a, b\}\) y\(\{a, c\}\) (solo hay uno; ¿qué es?) ,\(\ell' \subseteq \ell\text{.}\) El elemento menor de\(\mathcal{P}(A)\) es\(\emptyset\) y el elemento más grande es\(A=\{a, b, c\}\text{.}\) El diagrama de Hasse de este poset se muestra en la Figura\(\PageIndex{1}\).

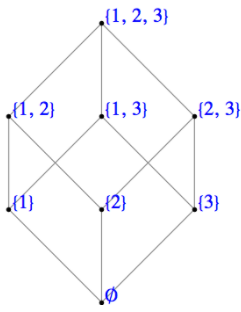Figura\(\PageIndex{1}\): Conjunto de potencia de\(\{1,\:2,\:3\}\)

Los ejemplos y definiciones anteriores indican que el límite menor superior y el mayor límite inferior se definen en términos del orden parcial del poset dado. Aún no está claro si todos los posets tienen la propiedad tal que cada par de elementos siempre tiene tanto un límite superior mínimo como un límite inferior mayor. En efecto, no es así (ver Ejercicio\(\PageIndex{1}\)).

Ejercicios

Ejercicio \(\PageIndex{1}\)

Considera el poset\((D_{30},\mid)\text{,}\) donde\(D_{30} = \{1,2, 3, 5, 6, 10, 15, 30\}\text{.}\)

1. Encuentra todos los límites inferiores de 10 y 15.
2. Encuentra el mayor límite inferior de 10 y 15.
3. Encuentra todos los límites superiores de 10 y 15.
4. Determinar el límite superior mínimo de 10 y 15.
5. Dibuja el diagrama de Hasse para\(D_{30}\) con respecto a\(\mid\text{.}\) Comparar este diagrama de Hasse con el de Ejemplo\(\PageIndex{3}\). Tenga en cuenta que los dos diagramas son estructuralmente iguales.

Contestar

1. 1, 5
2. 5
3. 30
4. 30
5. Vea la celda de Sage a continuación con la entrada predeterminada que muestra un diagrama de Hasse para\(D_{12}\text{.}\)

Ejercicio\(\PageIndex{2}\)

Enumere los elementos de los conjuntos\(D_8\text{,}\)\(D_{50}\text{,}\) y\(D_{1001}\text{.}\) Para cada conjunto, dibuje el diagrama de Hasse para “divide”.

Ejercicio \(\PageIndex{3}\)

La figura\(\PageIndex{2}\) contiene diagramas de Hasse de posets.

1. Determinar el mínimo límite superior y el límite inferior mayor de todos los pares de elementos cuando existan. Indicar aquellos pares que no tengan un límite superior mínimo (o un límite inferior mayor).
2. Encuentra los elementos menos y mayores cuando existen.

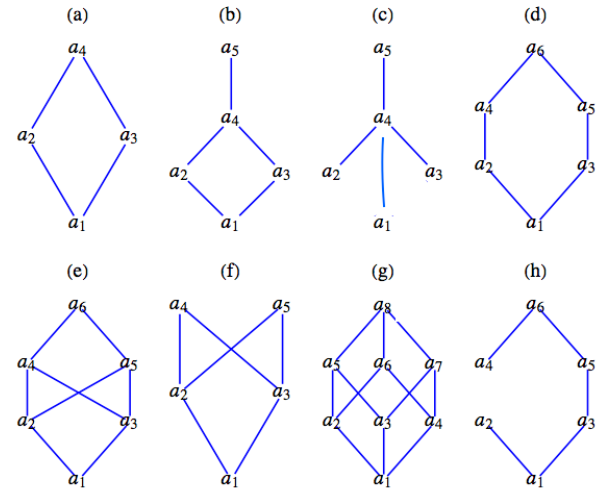Figura\(\PageIndex{2}\): Figura para el ejercicio\(\PageIndex{3}\)

Contestar

• Solución para el diagrama de Hasse (b):
  • \ begin {ecuación*}\ begin {array} {c|c}\ begin {array} {c|ccccc}\ lor &a_1 & a_2 & a_3 & a_4 & a_5\\ hline a_1 & a_1 &a_2 & a_3 & a_4 & a_5\\ a_2 & a_2 & a_2 & a_2 & a_4 & a_4 & a_5\ a_3 & a_3 & a_3 & a_4 y a_3 y a_4 y a_5\\ a_4 y a_4 y a _4 & a_4 & a_4 & a_5\\ a_5 & a_5 & a_5 & a_5 & a_5 & a_5 & a_5\\ end {array} &\ quad\ begin {array} {c|ccccc}\ land & a_1 & a_2 & a_3 & a_4 & a_5\\ hline a_1 & a_1 & a_1 & a_1 & a_1 & a_1\ a_2 & a_1 y a_2 y a_1 y a_2 y a_2 \\ a_3 & a_1 & a_1 & a_3 & a_3 & a_3\\ a_3\ a_4 & a_1 & a_2 & a_3 & a_4 & a_4\\ a_5 & a_1 & a_2 & a_3 & a_4 & a_5\\ end {array}\ end {array}\ end {equation*}
    \(a_1\) es el elemento menor y\(a_5\) es el elemento más grande.
• Solución parcial para el diagrama de Hasse (f):
  • \(\textrm{ lub}\left(a_2, a_3\right)\)y\(\textrm{ lub}\left( a_4,a_5\right)\) no existen.
  • No existe ningún elemento mayor, sino\(a_1\) que es el elemento menor.

Ejercicio\(\PageIndex{4}\)

Para el poset\((\mathbb{N},\leq )\text{,}\) ¿cuáles son el mayor límite inferior y el límite menor superior de dos elementos\(a\) y\(b\text{?}\) ¿hay elementos menores y/o mayores?

Ejercicio\(\PageIndex{5}\)

1. Demostrar la segunda parte del Teorema\(\PageIndex{1}\), el límite inferior superior de dos elementos en un poset es único, existe uno.
2. Demostrar que si un poset\(L\) tiene un elemento mínimo, entonces ese elemento es único.

Contestar

Si\(0\) y\(0'\) son menos elementos distintos, entonces

\ begin {ecuación*}\ left. \ begin {array} {cc} 0\ leq 0' &\ textrm {since} 0\ textrm {es un elemento mínimo}\\ 0'\ leq 0 &\ textrm {desde} 0'\ textrm {es un elemento mínimo}\\\ end {array}\ right\}\ Rightarrow 0=0'\ textrm {por antisimetría, una contradicción}\ fin {ecuación*}

Ejercicio\(\PageIndex{6}\)

Naturalmente ordenamos los números\(A_m = \{1, 2, . . . , m\}\) con “menor o igual a”, que es un orden parcial. Definimos un orden,\(\preceq\) sobre los elementos de\(A_m \times A_n\) por

\ begin {ecuación*} (a, b)\ preceq (a', b')\ Leftrightarrow a\ leq a'\ textrm {y} b\ leq b'\ end {ecuación*}

1. Demostrar que\(\preceq\) es un orden parcial en\(A_m \times A_n\text{.}\)
2. Dibuje los diagramas de orden para\(\preceq\) encendido\(A_2 \times A_2\text{,}\)\(A_2\times A_3\text{,}\) y\(A_3 \times A_3\text{.}\)
3. En general, ¿cómo se determina el mínimo límite superior y el límite inferior más grande de dos elementos de\(A_m \times A_n\text{,}\)\((a, b)\) y\((a',b')\text{?}\)
4. ¿Hay menos y/o mayores elementos en\(A_m \times A_n\text{?}\)

Ejercicio\(\PageIndex{7}\)

\(\mathcal{P}_0\)Sea el conjunto de todos los subconjuntos\(T\) de\(S = \{ 1, 2, \ldots, 9 \}\) tal manera que la suma de los elementos en\(T\) sea par. (Tenga en cuenta que el conjunto vacío se\(\emptyset\) incluirá como un elemento de\(\mathcal{P}_0\text{.}\)) Por ejemplo,\(\{ 2, 3, 6, 7 \}\) está en\(\mathcal{P}_0\) porque\(2+3+6+7\) es par, pero no\(\{1, 3, 5, 6\}\) está en\(\mathcal{P}_0\) porque\(1+3+5+6\) es impar. Considerar el poset\((\mathcal{P}_0, \subseteq)\text{.}\) Let\(A = \{ 1, 2, 3, 6 \}\) y\(B = \{ 2, 3, 6, 7 \}\) ser elementos de\(\mathcal{P}_0\text{.}\)

1. \(A \cap B \)Explique por qué no es elemento del poset.
2. Utilice las definiciones de los términos en cursiva y el orden parcial dado para completar las siguientes declaraciones:
   1. \(R \in \mathcal{P}_0\)es un límite superior de\(A\) y\(B\) si\ regla {3cm} {0.01cm}
   2. \(R \in \mathcal{P}_0\)es el elemento mínimo de\(\mathcal{P}_0\) if\ rule {3cm} {0.01cm}
3. Encuentra tres límites superiores diferentes de\(A\) y\(B\text{.}\)
4. Encuentra el límite inferior superior de\(A\) y\(B\text{.}\) Si no existe, explica por qué no.

Contestar

1. La suma de elementos en\(A∩B=\{2,\:3,\:6\}\) es impar y descalifica al conjunto de ser un elemento del poset.
2. Utilice las definiciones de los términos en cursiva y el orden parcial dado para completar las siguientes declaraciones:
   1. \(…A⊆R\)y\(B⊆R\)
   2. \(…\)para todos\(A∈\mathcal{P}_0\),\(R⊆A\)
3. Cualquier conjunto que contenga la unión de\(A∪B=\{1,\:2,\:3,\:6,\:7\}\) pero que también contenga 3 o 5, pero no ambos será un límite superior. Puedes crear varios incluyendo en no incluir 4 u 8.
4. El límite inferior superior no existe. Observe que la unión de\(A\) y\(B\) no está en\(\mathcal{P}_0\). Uno de los dos conjuntos\(\{1,\:2,\:3,\:5,\:6,\:7\}\) y\(\{1,\:2,\:3,\:6,\:7,\:9\}\) está contenido dentro de cada límite superior de A y B pero ninguno está contenido dentro del otro.