13.7: Una breve introducción a la teoría del cambio y el diseño lógico

Última actualización
Guardar como PDF

Page ID: 117181

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Renuncia

Sigo buscando una buena aplicación para dibujar puertas lógicas. Las cifras aquí son bastante ásperas.

Las primeras computadoras dependían de muchos conmutadores para realizar las operaciones lógicas necesarias para el cálculo. Esto fue cierto ya en la década de 1970 cuando empezaron a aparecer computadoras personales tempranas como la Altair (Figura$\PageIndex{1}$). Científicos pioneros en computación como Claude Shannon se dieron cuenta de que el funcionamiento de estas computadoras podría simplificarse haciendo uso de un isomorfismo entre los circuitos informáticos y el álgebra booleana. En ese momento se utilizó el término Teoría del Cambio. Las puertas lógicas realizadas a través de circuitos integrados cada vez más pequeños siguen desempeñando las mismas funciones que en las primeras computadoras, pero utilizando medios puramente electrónicos. En esta sección, damos ejemplos de algunos circuitos de conmutación. Poco después, haremos la transición a la forma más moderna de circuitos que se estudian en Logic Design, donde las puertas reemplazan a los interruptores. Nuestro principal objetivo es darle una visión general de cómo las funciones booleanas corresponden a cualquier circuito de este tipo. Introduciremos la notación del sistema común utilizada en el diseño lógico y mostraremos cómo se corresponde con la notación matemática de álgebras booleanas. Cualquier informático debe estar familiarizado con ambos sistemas.

$clipboard_e30b59b57a0fb157a6c841b67a781cdc7.png$ Figura$\PageIndex{1}$: La computadora Altair, una PC temprana, por Todd Dailey, Creative Commons

El dispositivo de conmutación más simple es el interruptor de encendido-apagado. Si el interruptor está cerrado/encendido, la corriente pasará a través de él; si está abierto/apagado, la corriente no pasará a través de él. Si designamos ON por 1, y OFF por 0, podemos describir circuitos eléctricos que contienen interruptores mediante expresiones booleanas con las variables que representan los estados variables de los conmutadores o los bits variables que pasan a través de puertas.

La electrónica involucrada en estos interruptores toma en cuenta si estamos negando un interruptor o no. Para los interruptores electromagnéticos, se utiliza un imán para controlar si el interruptor está abierto o cerrado. Los propios imanes pueden ser controlados por simples interruptores de encendido/apagado. Hay dos tipos de interruptores electromagnéticos. Uno normalmente está abierto (APAGADO) cuando el imán no está activado, pero al activar el imán se cerrará el circuito y el interruptor se ENCENDIDO. Un tipo separado de interruptor corresponde con un interruptor negado. Para ese tipo, el interruptor se cierra cuando el imán no está activado, y cuando el imán está activado, el interruptor se abre. No nos preocuparemos demasiado por los detalles de estos interruptores o la electrónica correspondiente a las puertas lógicas. Simplemente asumiremos que están disponibles para enchufar a un circuito. Para simplificar, utilizamos el símbolo de inversión en una variable que etiqueta un switch para indicar que es un conmutador del segundo tipo, como en la Figura$\PageIndex{3}$.

Nota$\PageIndex{1}$

Los generadores de energía de reserva que muchas personas tienen en sus hogares utilizan un interruptor de transferencia para conectar el generador al sistema de energía del hogar. Este interruptor está abierto (OFF) si hay alimentación proveniente de la fuente de alimentación municipal normal. Se mantiene APAGADO porque un imán lo mantiene abierto. Cuando se pierde la alimentación, el imán ya no se activa, y el interruptor se cierra y está ENCENDIDO. Entonces, el interruptor de transferencia es un interruptor normalmente ON.

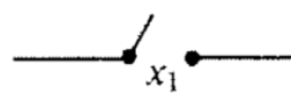$clipboard_e65a454c5e9c983a75104ce36292eaec6.png$ Figura$\PageIndex{2}$: Representación de un interruptor normalmente OFF controlado por variable$x_1$

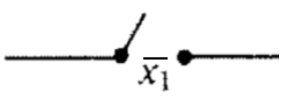$clipboard_e991600d5fa7fe52a0da0bfb78a8a5416.png$ Figura$\PageIndex{3}$: Representación de un conmutador normalmente ON controlado por variable$x_1$

La notación estándar utilizada para las operaciones de álgebra booleana en la teoría de conmutación y el diseño lógico es$+$ para unir, en lugar de$\lor \text{;}$ y$\cdot $ para meet, en lugar de$\land \text{.}$ Complementation es lo mismo en ambos sistemas notacionales, denotado con un overline.

La expresión$x_1 \cdot x_2$ representa la situación en la que una serie de dos interruptores aparece en secuencia como en la Figura$\PageIndex{4}$. Para que la corriente fluya a través del circuito, ambos interruptores deben estar ENCENDIDOS; es decir, ambos deben tener el valor 1. De igual manera, un par de conmutadores paralelos, como en la Figura$\PageIndex{5}$, se describe algebraicamente por$x_1 + x_2\text{.}$ Aquí, la corriente fluye a través de esta parte del circuito siempre que al menos el encendido de los interruptores esté ENCENDIDO.

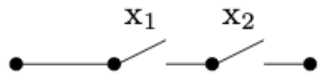$clipboard_eb8be893059beaaf9a8f9897e8c4d285e.png$ Figura$\PageIndex{4}$: Realización de dos conmutadores en configuración AND$x_1\cdot x_2$

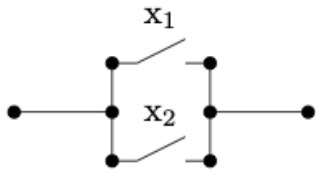$clipboard_e86811b5aa0993c2cb054031c99d7214b.png$ Figura$\PageIndex{5}$: Realización de dos conmutadores en configuración OR$x_1+x_2$

Todas las leyes y conceptos desarrollados previamente para álgebras booleanas se mantienen. El único cambio es puramente notacional. Realizamos el cambio en esta sección únicamente para introducir al lector a otro sistema de notación de uso frecuente.

Muchas de las leyes del álgebra booleana se pueden visualizar en teoría de cambio de pensamiento. Por ejemplo, la ley distributiva de meet over join se expresa como

\ begin {ecuación*} x_1\ cdot\ izquierda (x_2+ x_3\ derecha) = x_1\ cdot x_2+x_1\ cdot x_3. \ end {ecuación*}

El circuito de conmutación analógico de la afirmación anterior es que los circuitos en las dos imágenes a continuación son equivalentes. En el circuito (b), la presencia$x_1$ de dos podría representar dos interruptores electromagnéticos controlados por el mismo imán.

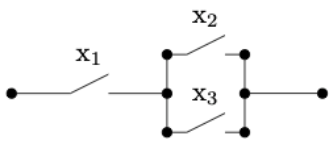$clipboard_eadd79a5f17cdac745924ea9e2046f6be.png$ Figura$\PageIndex{6}$: (a)

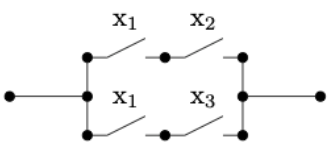$clipboard_ea7ced92f244cc3213f382c7cd3a4ebbe.png$ Figura$\PageIndex{7}$: (b)

Los circuitos en una computadora ahora están compuestos por grandes cantidades de puertas, que tienen el mismo propósito que los interruptores, pero pueden miniaturizarse en gran medida. Por ejemplo, la puerta OR, generalmente dibujada como en la Figura$\PageIndex{8}$ implementa la función lógica OR. Esto sucede electrónicamente, pero equivale a Figura$\PageIndex{5}$. La puerta AND, que equivale a dos interruptores secuenciales se muestra en la Figura$\PageIndex{8}$.

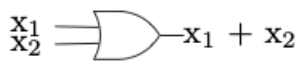$clipboard_e3947ae98932b81f8a208cc8baa458fce.png$ Figura$\PageIndex{8}$: Una puerta OR

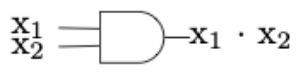$clipboard_e1146ffd91f55f939cd2a096c553124a2.png$ Figura$\PageIndex{9}$: Una puerta Y

El proceso de complementación se representa en un diagrama de puerta mediante un inversor, como se muestra en la Figura$\PageIndex{10}$.

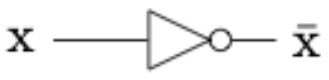$clipboard_ef4c413342130b23762e9309e104c4636.png$ Figura$\PageIndex{10}$: Inversor, o puerta NO

Al dibujar circuitos más complejos, a veces se representan múltiples AND u OR usando un dibujo de puerta más general. Por ejemplo, si queremos representar una puerta OR con tres entradas que esté ON siempre y cuando al menos una entrada esté ON, la dibujaríamos como en la Figura$\PageIndex{11}$, aunque esto realmente serían dos puertas binarias, como en la Figura$\PageIndex{12}$. Ambos diagramas están realizando la expresión booleana$x_1 + x_2 + x_3\text{.}$ Estrictamente hablando, las puertas en Figura$\PageIndex{12}$ representan$(x_1 + x_2 )+ x_3\text{,}$ pero la ley asociativa para unirse nos dice que la agrupación no importa.

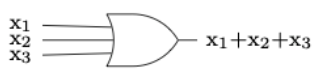$clipboard_e9f04af807d1162ac31cbc46572a78de5.png$ Figura$\PageIndex{11}$: Versión simple de una puerta OR ternaria

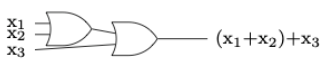$clipboard_e604c1850bb4b96dc046640a3fc4ffd30.png$ Figura$\PageIndex{12}$: Una puerta OR ternaria creada con puertas OR binarias

En la Figura$\PageIndex{13}$, mostramos algunas otras puertas de uso común, XOR, NAND y NOR, que corresponden a las exressiones booleanas$x_1 \oplus x_2\text{,}$$\overline{x_1 \cdot x_2}\text{,}$ y$\overline{x_1 + x_2}\text{,}$ respectivamente.

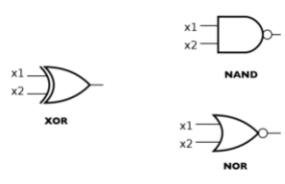$clipboard_e103a037e6a177dfb9a981178352021ff.png$ Figura$\PageIndex{13}$: Otras puertas comunes

Empecemos con un circuito lógico y veamos cómo las leyes del álgebra booleana pueden ayudarnos a simplificarlo.

Ejemplo$\PageIndex{1}$: Simplification of a Circuit

Considera el circuito en la Figura$\PageIndex{14}$. Como es habitual, suponemos que tres entradas entran por la izquierda y la salida sale por la derecha.

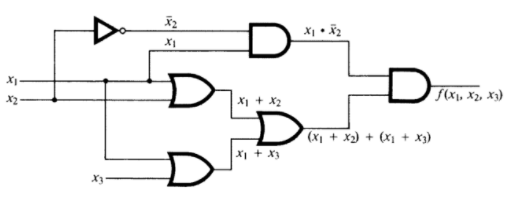$clipboard_ea34e928af5ef4528c6edb4f01d2e9e07.png$ Figura$\PageIndex{14}$: Diagrama de puerta inicial

Si trazamos las entradas a través de las puertas vemos que este circuito realiza la función booleana

\ begin {ecuación*} f\ izquierda (x_1, x_2, x_3\ derecha) =x_1\ cdot\ overline {x_2}\ cdot\ izquierda (\ izquierda (x_1 + x_2\ derecha) +\ izquierda (x_1 + x_3\ derecha)\ derecha). \ end {ecuación*}

Simplificamos la expresión booleana que define$f\text{,}$ simplificando el circuito al hacerlo. Debes ser capaz de identificar las leyes del álgebra booleana que se utilizan en cada uno de los pasos. Ver Ejercicio$\PageIndex{1}$.

\ begin {ecuación*}\ begin {split} x_1\ cdot\ overline {x_2}\ cdot\ izquierda (\ izquierda (x_1 + x_2\ derecha) +\ izquierda (x_1 + x_3\ derecha)\ derecha) & = x_1\ cdot\ overline {x_2}\ cdot\ izquierda (x_1+ x_2 + x_3\ derecha)\\ & = x_1\ cdot\ overline {x_2}\ cdot x_1 + x_1\ cdot\ overline {x_2}\ cdot x_2 + x_1\ cdot\ overline {x_2}\ cdot x_3\ & amp; = x_1\ cdot\ overline {x_2} + 0\ cdot x_1 + x_3\ cdot x_1\ cdot\ overline {x_2}\\ &=x_1\ cdot\ overline {x_2} + x_3\ cdot x_1\ cdot\ overline {x_2}\\ &= x_1\ cdot\ overline {x_2}\ cdot\ izquierda (1 + x_3\ derecha)\\ &= x_1\ cdot\ overline {x_2}\ end {split}\ end {equation*}

Por lo tanto,$f\left(x_1, x_2, x_3\right)=x_1 \cdot \overline{x_2}\text{,}$ que se puede realizar con el circuito mucho más simple de la Figura$\PageIndex{15}$, sin utilizar la entrada$x_3\text{.}$

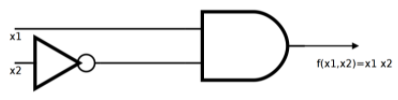$clipboard_e8bb2444f68a2f237bed476716f8e18be.png$ Figura$\PageIndex{15}$: Diagrama de puerta simplificado

A continuación, comenzamos con una tabla de salidas deseadas basada en tres bits de entrada y diseñamos un circuito eficiente para realizar esta salida.

Ejemplo$\PageIndex{2}$

Considere la siguiente tabla de salidas deseadas para los tres bits de entrada$x_1, x_2, x_3\text{.}$

Tabla$\PageIndex{1}$: Tabla de salida deseada

$x_1$	$x_2$	$x_3$	$f(x_1,\:x_2,\:x_3)$
\ (x_1\) ">$0$	\ (x_2\) ">$0$	\ (x_3\) ">$0$	\ (f (x_1,\ :x_2,\ :x_3)\) ">$0$
\ (x_1\) ">$0$	\ (x_2\) ">$0$	\ (x_3\) ">$1$	\ (f (x_1,\ :x_2,\ :x_3)\) ">$1$
\ (x_1\) ">$0$	\ (x_2\) ">$1$	\ (x_3\) ">$0$	\ (f (x_1,\ :x_2,\ :x_3)\) ">$0$
\ (x_1\) ">$0$	\ (x_2\) ">$1$	\ (x_3\) ">$1$	\ (f (x_1,\ :x_2,\ :x_3)\) ">$0$
\ (x_1\) ">$1$	\ (x_2\) ">$0$	\ (x_3\) ">$0$	\ (f (x_1,\ :x_2,\ :x_3)\) ">$1$
\ (x_1\) ">$1$	\ (x_2\) ">$0$	\ (x_3\) ">$1$	\ (f (x_1,\ :x_2,\ :x_3)\) ">$1$
\ (x_1\) ">$1$	\ (x_2\) ">$1$	\ (x_3\) ">$0$	\ (f (x_1,\ :x_2,\ :x_3)\) ">$0$
\ (x_1\) ">$1$	\ (x_2\) ">$1$	\ (x_3\) ">$1$	\ (f (x_1,\ :x_2,\ :x_3)\) ">$0$

El primer paso es escribir la Forma Normal Minterm, Definición 13.6.3, de$f\text{.}$ Dado que estamos trabajando con los dos valores álgebra booleana,$B_2\text{,}$ las constantes en cada minterm son 0 o 1, y simplemente enumeramos los minterms que tienen un 1. Estos corresponden con las filas de la tabla anterior que tienen una salida de 1. Entonces intentaremos simplificar la expresión tanto como sea posible.

\ begin {ecuation*}\ begin {split} f\ left (x_1, x_2, x_3\ right) &= (\ overline {x_1}\ cdot\ overline {x_2}\ cdot x_3) + (x_1\ cdot\ overline {x_2}\ cdot\ overline {x_3}) + (x_1\ cdot overline {x_3}) + (x_1\ cdot overline {x_3}) + (x_1\ cdot sobrelínea {x_2}\ cdot x_3)\\ &=\ overline {x_2}\ cdot ((\ overline {x_1}\ cdot x_3) + (x_1\ cdot\ overline {x_3}) + (x_1\ cdot x_3))\\ &= \ overline {x_2}\ cdot ((\ overline {x_1}\ cdot x_3) + x_1\ cdot (\ overline {x_3} + x_3))\\ &=\ overline {x_2}\ cdot ((\ overline {x_1}\ cdot x_3) + x_1)\\ end {split} end {ecuación*}

Por lo tanto podemos realizar nuestra tabla con la función booleana$f\left(x_1, x_2, x_3\right)=\overline{x_2} \cdot ((\overline{x_1} \cdot x_3) + x_1)\text{.}$ Un diagrama de circuito para esta función es Figura$\PageIndex{16}$. Pero, ¿es este el circuito más simple que realiza la mesa? Ver Ejercicio$\PageIndex{3}$.

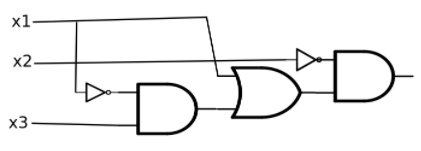$clipboard_e0956ec24a3d6e558840ea6f34ed66715.png$ Figura$\PageIndex{16}$: Una realización de la tabla de salidas deseadas.

13.7.1: Ejercicios

Ejercicio$\PageIndex{1}$

Enumere las leyes del álgebra booleana que justifican los pasos en la simplificación de la función booleana$f\left(x_1, x_2, x_3\right)$ en Ejemplo$\PageIndex{1}$. Algunos pasos utilizan más de una ley.

Contestar

Leyes asociativas, conmutativas e idempotentes.
Derecho distributivo.
Leyes idempotentes y de complemento.
Leyes nulas y de identidad
Derecho distributivo.
Leyes nulas y de identidad.

Ejercicio$\PageIndex{2}$

Escribe la siguiente expresión booleana en la notación de diseño lógico.

\ begin {ecuation*}\ left (x_1\ land\ overline {x_2}\ right)\ lor\ left (x_1\ land x_2\ right)\ lor\ left (\ overline {x_1}\ land x_2\ right). \ end {ecuación*}

Contestar: \ begin {ecuación*} (x_1\ cdot\ overline {x_2}) + (x_1\ cdot x_2) + (\ overline {x_1}\ cdot x_2). \ end {ecuación*}

Ejercicio$\PageIndex{3}$

Encuentre una simplificación adicional de la función booleana en Ejemplo$\PageIndex{2}$, y dibuje el diagrama de puerta correspondiente para el circuito que realiza.

Contestar: Una expresión booleana más simple para la función es$\overline{x_2} \cdot (x_1 + x_3)\text{.}$

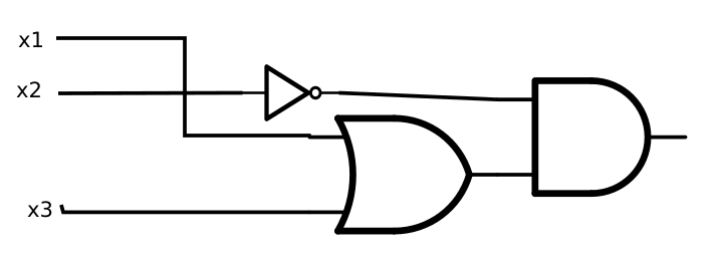$clipboard_ef0040540718705cba2eae273dc9e7dad.png$ Figura$\PageIndex{17}$: Un circuito aún más simple

Ejercicio$\PageIndex{4}$

Considere el circuito de conmutación en la Figura$\PageIndex{18}$.

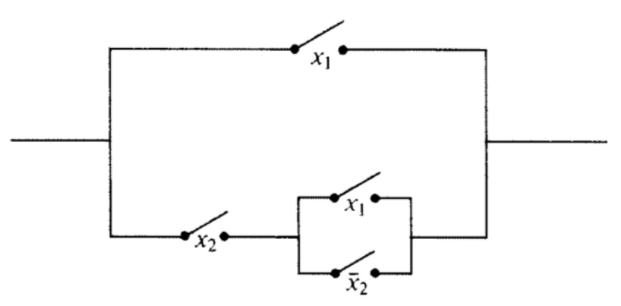$clipboard_e9a89840fad6e18dc5cbfea346987cea6.png$ Figura$\PageIndex{18}$: ¿Se puede simplificar este circuito?

Dibuja el diagrama de puerta correspondiente para este circuito.
Construir una tabla de salidas para cada una de las ocho entradas a este circuito.
Determinar la normal minterm de la función booleana basada en la tabla.
Simplifica el circuito tanto como sea posible.

Ejercicio$\PageIndex{5}$

Considera el circuito en la Figura$\PageIndex{19}$.

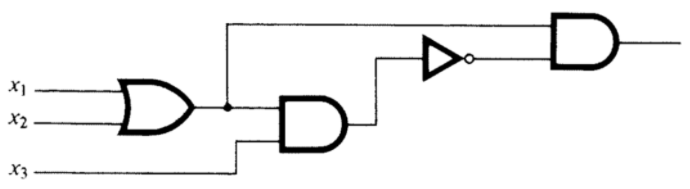$clipboard_e08381e8c7a21b5dbce7d0b8f37816fe9.png$ Figura$\PageIndex{19}$: ¿Se puede simplificar este circuito?

Rastree las entradas a través de este circuito y determine la función booleana que realiza.
Construir una tabla de salidas para cada una de las ocho entradas a este circuito.
Encuentra la forma normal minterm de$f\text{.}$
Dibuja el circuito basado en la forma normal minterm.
Simplifica el circuito algebraicamente y dibuja el circuito resultante.

Ejercicio$\PageIndex{6}$

Considere la función booleana$f\left(x_1, x_2, x_3, x_4\right)=x_1 + \left(x_2 \cdot \left(\overline{x_1} + x_4\right) + x_3 \cdot \left(\overline{x_2} + \overline{x_4}\right)\right).$

Simplificar$f$ algebraicamente.
Dibuje el diagrama de puerta basado en la versión simplificada de$f\text{.}$

Ejercicio$\PageIndex{7}$

Dibuja un circuito lógico usando solo puertas AND, OR y NOT que realice una puerta XOR.

Ejercicio$\PageIndex{8}$

Dibuja un circuito lógico usando solo puertas AND, OR y NOT que realice la función booleana en tres variables que devuelva 1 si la mayoría de las entradas son 1 y 0 de lo contrario.

\(x_1\)	\(x_2\)	\(x_3\)	\(f(x_1,\:x_2,\:x_3)\)
\ (x_1\) ">\(0\)	\ (x_2\) ">\(0\)	\ (x_3\) ">\(0\)	\ (f (x_1,\ :x_2,\ :x_3)\) ">\(0\)
\ (x_1\) ">\(0\)	\ (x_2\) ">\(0\)	\ (x_3\) ">\(1\)	\ (f (x_1,\ :x_2,\ :x_3)\) ">\(1\)
\ (x_1\) ">\(0\)	\ (x_2\) ">\(1\)	\ (x_3\) ">\(0\)	\ (f (x_1,\ :x_2,\ :x_3)\) ">\(0\)
\ (x_1\) ">\(0\)	\ (x_2\) ">\(1\)	\ (x_3\) ">\(1\)	\ (f (x_1,\ :x_2,\ :x_3)\) ">\(0\)
\ (x_1\) ">\(1\)	\ (x_2\) ">\(0\)	\ (x_3\) ">\(0\)	\ (f (x_1,\ :x_2,\ :x_3)\) ">\(1\)
\ (x_1\) ">\(1\)	\ (x_2\) ">\(0\)	\ (x_3\) ">\(1\)	\ (f (x_1,\ :x_2,\ :x_3)\) ">\(1\)
\ (x_1\) ">\(1\)	\ (x_2\) ">\(1\)	\ (x_3\) ">\(0\)	\ (f (x_1,\ :x_2,\ :x_3)\) ">\(0\)
\ (x_1\) ">\(1\)	\ (x_2\) ">\(1\)	\ (x_3\) ">\(1\)	\ (f (x_1,\ :x_2,\ :x_3)\) ">\(0\)