13.6: Expresiones booleanas

En esta sección, utilizaremos nuestros antecedentes de las secciones anteriores y la teoría de conjuntos para desarrollar un procedimiento para simplificar las expresiones booleanas. Este procedimiento tiene una aplicación considerable a la simplificación de circuitos en teoría de conmutación o diseño lógico.

Definición$\PageIndex{1}$: Boolean Expression

Dejar$[B; \lor , \land, - ]$ ser cualquier álgebra booleana, y dejar$x_1, x_2, \ldots , x_k$ ser variables en$B\text{;}$ esto es, variables que pueden asumir valores de$B\text{.}$ Una expresión booleana generada por$x_1, x_2, \ldots , x_k$ es cualquier combinación válida de los$x_i$ y los elementos de$B$ con las operaciones de meet, join, y complementación.

Esta definición es el análogo de la definición de una proposición generada por un conjunto de proposiciones, presentada en la Sección 3.2.

Cada expresión booleana generada por$k$ variables,$e\left(x_1, \ldots , x_k\right)\text{,}$ define una función$f: B^k \to B$ donde$f\left(a_1,\ldots , a_k\right)=e\left(a_1, \ldots , a_k\right)\text{.}$ Si$B$ es un álgebra booleana finita, entonces hay un número finito de funciones desde$B^k$ dentro$B\text{.}$ Esas funciones que se definen en términos de expresiones booleanas son llamadas funciones booleanas. Como veremos, hay un número infinito de expresiones booleanas que definen cada función booleana. Naturalmente, se preferirá la “más corta” de estas expresiones. Dado que los circuitos electrónicos pueden describirse como funciones booleanas con$B=B_2\text{,}$ esta economización es bastante útil.

En lo que sigue, hacemos uso del Ejercicio 7.1.5 de la Sección 7.1 para contar el número de funciones.

Ejemplo$\PageIndex{1}$: Two Variables Over $B_{2}$

Considera algún álgebra booleana de orden 2,$[B; \lor, \land, - ]\text{.}$ ¿Cuántas funciones$f:B^2\to B$ hay? Primero, todas las álgebras booleanas de orden 2 son isomórficas a$\left[B_2; \lor , \land, - \right]$ así que queremos determinar el número de funciones$f:B_2^2\to B_2\text{.}$ si consideramos una función booleana de dos variables,$x_1$ y$x_2\text{,}$ observamos que cada variable tiene dos valores posibles 0 y 1, por lo que hay$2^2$ formas de asignar estos dos valores a las$k=2$ variables. De ahí que la siguiente tabla tenga$2^2=4$ filas. Hasta el momento tenemos una mesa como ésta:

\ begin {ecuación*}\ begin {array} {cc|c} x_1 & x_2 & f\ left (x_1, x_2\ derecha)\\\ hline 0 & 0 &? \\ 0 & 1 &? \\ 1 & 0 &? \\ 1 & 1 &? \\\ end {array}\ end {ecuación*}

¿Cuántas posibles funciones diferentes puede haber? Para enumerar algunos:$f_1\left(x_1, x_2\right)=x_1\text{,}$$f_2\left(x_1, x_2\right)=x_2\text{,}$$f_3\left(x_1, x_2\right)=x_1\lor x_2\text{,}$$f_4\left(x_1, x_2\right)=\left(x_1\land \overline{x_2}\right)\lor x_2\text{,}$$f_5\left(x_1, x_2\right)= x_1\land x_2\lor \overline{x_2}\text{,}$ etc. Cada uno de estos rellenará los signos de interrogación en la tabla anterior. Las mesas para$f_1\textrm{ }$ y$f_3$ son

\ begin {ecuación*}\ begin {array} {lr}\ begin {array} {cc|c} x_1 & x_2 & f_1\ left (x_1, x_2\ derecha)\\\ hline 0 & 0 & 0\\ 0 & 1 & 0\\ 1 & 0 & 1\\ 1 & 1 & 1 & 1\\\ end {array} &\ begin {array} {cc|c} x_1 y x_2 y f_3\ izquierda (x_1, x_2\ derecha)\\ hline 0 & 0 & 0\\ 0 & 1 & amp; 1\\ 1 & 0 & 1\\ 1 & 1 & 1 & 1\\\ end {array}\\ end {array}\ end {equation*}

Dos funciones son diferentes si y solo si sus tablas son diferentes para al menos una fila. Por supuesto mediante el uso de las leyes básicas del álgebra booleana podemos ver que$f_3=f_4\text{.}$ ¿Por qué? Entonces, si simplemente enumeramos por fuerza bruta todas las “combinaciones” de$x_1 \textrm{ and } x_2$ obtendremos duplicaciones innecesarias. Sin embargo, observamos que para cualquier combinación de las variables$x_1\text{,}$ y solo$x_2$ hay dos valores posibles para$f\left(x_1, x_2\right)\text{,}$ saber 0 o 1. Así, podríamos escribir$2^4=16$ diferentes funciones en 2 variables.

Ahora, vamos a contar el número de diferentes funciones booleanas en un entorno más general. Consideraremos dos casos: primero, cuándo y segundo$B=B_2$, cuándo$B$ es cualquier álgebra booleana finita con$2^n$ elementos.

Let$B=B_2\text{.}$ Cada función$f:B^k\to B$ se define en términos de una tabla que tiene$2^k$ filas. Por lo tanto, dado que hay dos posibles imágenes para cada elemento de$B^k\text{,}$ hay 2 elevadas a las funciones$2^k\text{,}$ o$2^{2^k}$ diferentes. Mostraremos que cada una de estas funciones es una función booleana.

Ahora supongamos que$\lvert B\rvert =2^n>2\text{.}$ Una función de$B^k$ hacia$B$ adentro todavía se puede definir en términos de una tabla. Hay$\lvert B\rvert^k$ filas en cada tabla y$\lvert B\rvert$ posibles imágenes para cada fila. Por lo tanto, se$2^n$ elevan al poder$2^{nk}$ diferentes funciones. Mostraremos que si$n>1\text{,}$ no cada una de estas funciones es una función booleana.

Dado que todos los álgebras booleanos son isomórficos a un álgebra booleana de conjuntos, los análogos de declaraciones en conjuntos son útiles en álgebras booleanas.

Definición $\PageIndex{2}$: Minterm

Una expresión booleana generada por$x_1, x_2, \ldots , x_k$ que tiene la forma

\ begin {ecuación*}\ underset {i=1} {\ overset {k} {\ land}} y_i,\ end {ecuación*}

donde cada uno$y_i$ puede ser$x_i$ o$\overline{x_i}$ se llama un minterm generado por$x_1, x_2, \ldots , x_k\text{.}$ Utilizamos la notación$M_{\delta_1 \delta_2 \cdots \delta_k}$ para el minterm generado por$x_1, x_2, \ldots , x_k\text{,}$ donde$y_i=x_i$ si$\delta_i = 1$ y$y_i=\bar{x_i}$ si$\delta_i = 0$

Un ejemplo de la notación es que$M_{110} = x_1 \land x_2 \land \bar{x_3}\text{.}$

Por una aplicación directa de la Regla de Productos vemos que existen$2^k$ diferentes minterms generados por$x_1, \ldots , x_k\text{.}$

Definición $\PageIndex{3}$: Minterm Normal Form

Una expresión booleana generada por$x_1, \ldots , x_k$ está en forma normal minterm si es la unión de expresiones de la forma$a \land m\text{,}$ donde$a\in B$ y$m$ es un minterm generado por Es$x_1, \ldots , x_k\text{.}$ decir, es de la forma

$$\label{eq:1} \underset{j=1}{\overset{p}{\lor }}\left(a_j\land m_j\right)$$

donde$p=2^k\text{,}$ y$m_1,m_2, \ldots , m_p$ son los minterms generados por$x_1, \ldots, x_k\text{.}$

Nota$\PageIndex{1}$

• Parece que requerimos cada minterm generado por$x_1, \ldots, x_k\text{,}$ in$\eqref{eq:1}$, y realmente lo hacemos. Sin embargo, algunos de los valores de$a_j$ pueden ser los$\pmb{0}\text{,}$ que efectivamente hacen desaparecer al minterm correspondiente.
• Si$B=B_2\text{,}$ entonces cada uno$a_j$ en una forma normal minterm es 0 o 1. Por lo tanto,$a_j\land m_j$ es 0 o$m_j\text{.}$

Teorema$\PageIndex{1}$: Uniqueness of Minterm Normal Form

Let$e\left(x_1,\ldots , x_k\right)$ be a booleana expresión sobre B. Existe una forma normal minterm única$M\left(x_1, \ldots , x_k\right)$ que es equivalente a$e\left(x_1, \ldots , x_k\right)$ en el sentido de que e y M definen la misma función desde$B^k$ dentro$B\text{.}$

La singularidad en este teorema no incluye el posible ordenamiento de los minterms en$M$ (comúnmente conocido como “singularidad hasta el orden de minterms”). La prueba de este teorema sería bastante larga, y no muy instructiva, por lo que dejaremos que el lector interesado lo intente. Las implicaciones del teorema son muy interesantes, sin embargo.

Si$\lvert B\rvert =2^n\text{,}$ entonces se$2^n$ elevan a las$2^k$ diferentes formas normales minterm. Dado que cada forma normal minterm diferente define una función diferente, hay un número similar de funciones booleanas desde$B^k$ dentro$B\text{.}$ Si$B=B_2\text{,}$ hay tantas funciones booleanas (2 elevadas a la$2^k$) como funciones desde$B^k$ dentro$B\text{,}$ ya que hay $2$elevado a las$2^{n}$ funciones desde$B^k$ hacia$B\text{.}$ La importancia de este resultado es que cualquier función deseada puede realizarse utilizando circuitos electrónicos que tengan valores 0 o 1 (apagado o encendido, positivo o negativo).

Los circuitos multivalores más complejos correspondientes a álgebras booleanas con más de dos valores no tendrían esta flexibilidad debido al número de formas normales minterm, y de ahí el número de funciones booleanas, es estrictamente menor que el número de funciones.

Cerraremos esta sección examinando las formas normales minterm para expresiones terminadas$B_2$, ya que son un punto de partida para la economización de circuitos.

Ejemplo$\PageIndex{2}$

Considerar la expresión booleana$f\left(x_1, x_2\right) =x_1 \lor \overline{x_2} \text{.}$ Un método para determinar la forma normal minterm de$f$ es pensar en términos de conjuntos. Considera el diagrama con la traducción habitual de notación en la Figura$\PageIndex{1}$. Entonces

\ begin {equation*}\ begin {split} f\ left (x_1, x_2\ right) &=\ left (\ overline {x_1}\ land\ overline {x_2}\ right)\ lor\ left (x_1\ land\ overline {x_2}\ right)\ lor\ left (x_1\ land x_2\ right)\\ & = M_ {00}\ or M_ {10}\ or M_ {11}\ final {división}\ final {ecuación*}

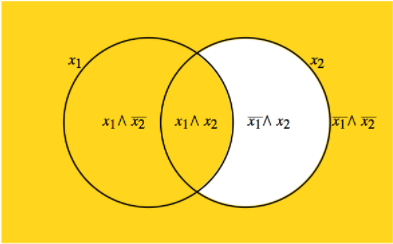Figura$\PageIndex{1}$: Visualización de minterms para$x_1\lor\bar{x_2}$

Tabla$\PageIndex{1}$: Definición de la función booleana$g$

$x_1$	$x_2$	$x_3$	$g(x_1,x_2,x_3)$
\ (x_1\) ">$0$	\ (x_2\) ">$0$	\ (x_3\) ">$0$	\ (g (x_1, x_2, x_3)\) ">$1$
\ (x_1\) ">$0$	\ (x_2\) ">$0$	\ (x_3\) ">$1$	\ (g (x_1, x_2, x_3)\) ">$0$
\ (x_1\) ">$0$	\ (x_2\) ">$1$	\ (x_3\) ">$0$	\ (g (x_1, x_2, x_3)\) ">$0$
\ (x_1\) ">$0$	\ (x_2\) ">$1$	\ (x_3\) ">$1$	\ (g (x_1, x_2, x_3)\) ">$1$
\ (x_1\) ">$1$	\ (x_2\) ">$0$	\ (x_3\) ">$0$	\ (g (x_1, x_2, x_3)\) ">$0$
\ (x_1\) ">$1$	\ (x_2\) ">$0$	\ (x_3\) ">$1$	\ (g (x_1, x_2, x_3)\) ">$0$
\ (x_1\) ">$1$	\ (x_2\) ">$1$	\ (x_3\) ">$0$	\ (g (x_1, x_2, x_3)\) ">$1$
\ (x_1\) ">$1$	\ (x_2\) ">$1$	\ (x_3\) ">$1$	\ (g (x_1, x_2, x_3)\) ">$0$

Ejemplo$\PageIndex{3}$

Considera la función$g:B_2^3 \to B_2$ definida por Table$\PageIndex{1}$.

La forma normal minterm para se$g$ puede obtener tomando la unión de minterms que corresponden a filas que tienen un valor de imagen de 1. Si$g\left(a_1, a_2, a_3\right)=1\text{,}$ entonces incluye el minterm$y_1\land y_2\land y_3$ donde

\ begin {ecuation*} y_j=\ begin {cases} x_j &\ textrm {if} a_j=1\\\ bar {x_j} &\ textrm {if} a_j=0\\\ end {casos}\ end {ecuación*}

O, para usar notación alternativa, incluir$M_{a_1a_2a_3}$ en la expresión if y solo si$g\left(a_1, a_2, a_3\right)=1$

Por lo tanto,

\ begin {ecuación*} g\ izquierda (x_1, x_2, x_3\ derecha) =\ izquierda (\ overline {x_1}\ tierra\ overline {x_2}\ tierra\ overline {x_3}\ derecha)\ lor\ izquierda (\ overline {x_1}\ tierra x_2\ tierra x_3\ derecha)\ lor\ izquierda (x_1\ tierra x_2\ tierra x_3\ derecha)\ lor\ izquierda (x_1\ tierra x_1} _2\ tierra\ overline {x_3}\ derecha). \ end {ecuación*}

La forma normal minterm es un primer paso para obtener una forma económica de expresar una función booleana dada. Para funciones de más de tres variables, el enfoque de teoría de conjuntos anterior tiende a ser incómodo. Se utilizan otros procedimientos para escribir la forma normal. El más conveniente es el mapa de Karnaugh, una discusión del cual se puede encontrar en cualquier texto lógico de teoría de diseño/cambio (ver, por ejemplo, [18]), en Wikipedia.

Ejercicios

Ejercicio$\PageIndex{1}$

1. Escribe las 16 posibles funciones de Ejemplo$\PageIndex{1}$.
2. Escribe las tablas de varias de las funciones booleanas anteriores para demostrar que efectivamente son diferentes.
3. Determinar las formas normales minterm de
   1. $\displaystyle g_1\left(x_1, x_2\right)=x_1\lor x_2,$
   2. $\displaystyle g_2\left(x_1, x_2\right)=\overline{x_1}\lor \overline{x_2}$
   3. $\displaystyle g_3\left(x_1, x_2\right)=\overline{x_1 \land x_2}$
   4. $\displaystyle g_4\left(x_1, x_2\right)=1$

Responder

1. $\displaystyle \begin{array}{l} f_1\left(x_1,x_2\right)=0 \\ f_2\left(x_1,x_2\right)=\left(\overline{x_1}\land \overline{x_2}\right) \\ f_3\left(x_1,x_2\right)=\left(\overline{x_1}\land x_2\right) \\ f_4\left(x_1,x_2\right)=\left(x_1\land \overline{x_2}\right) \\ f_5\left(x_1,x_2\right)=\left(x_1\land x_2\right) \\ f_6\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\right)=\overline{x_1} \\ f_7\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(x_1\land \overline{x_2}\right)\right)=\overline{x_2} \\ f_8\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=\left(\left(x_1\land x_2\right)\lor \left(\overline{x_1}\land \overline{x_2}\right)\right) \\ f_9\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land x_2\right)\lor \left(x_1\land \overline{x_2}\right)\right)=\left(\left(x_1\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\right) \\ f_{10}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land x_2\right)\lor \left(x_1\land x_2\right)\right)=x_2 \\ f_{11}\left(x_1,x_2\right)=\left(\left(x_1\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=x_1 \\ f_{12}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\lor \left(x_1\land \overline{x_2}\right)\right)=\left(\overline{x_1}\lor \overline{x_2}\right) \\ f_{13}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\lor \left(x_1\land x_2\right)\right)=\left(\overline{x_1}\lor x_2\right) \\ f_{14}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(x_1\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=\left(x_1\lor \overline{x_2}\right) \\ f_{15}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land x_2\right)\lor \left(x_1\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=\left(x_1\lor x_2\right) \\ f_{16}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\lor \left(x_1\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=1 \\ \end{array}$
2. La tabla de verdad para las funciones en la parte (a) son
   \ begin {ecuation*}\ begin {array} {llllllllll} x_1 & x_2 & f_1 & f_2 & f_3 & f_4 & f_5 & f_6 & f_7 & f_8\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1\\ 0 & 1 & 1\ 0 & 1\ 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1\\ end {array}\ end {equation*}
   \ begin {ecuación*}\ begin {array} {llllllllll} x_1 y x_2 & f_9 & f_ {10} & f_ {11} & f_ {12} & f_ {13} & f_ {14} & f_ {15} & f_ {16}\\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 1 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 1 & 1\\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 1 & 1 & 1 & 1 & 1\\ end {array}\ end {ecuación*}
3. 1. $\displaystyle g_1\left(x_1,x_2\right)=f_{15}\left(x_1,x_2\right)$
   2. $\displaystyle g_2\left(x_1,x_2\right)=f_{12}\left(x_1,x_2\right)$
   3. $\displaystyle g_3\left(x_1,x_2\right)=f_{12}\left(x_1,x_2\right)$
   4. $\displaystyle g_4\left(x_1,x_2\right)=f_{16}\left(x_1,x_2\right)$

Ejercicio$\PageIndex{2}$

Considere la expresión booleana$f\left(x_1, x_2, x_3\right)=\left(\overline{x_3}\land x_2\right)\lor\left(\overline{x_1}\land x_3\right)\lor \left(x_2\land x_3\right)$ en$\left[B_2^3; \lor, \land, - \right].$

1. Simplifica esta expresión usando leyes básicas de álgebra booleana.
2. Escribe esta expresión en forma normal minterm.
3. Escriba la tabla para la función dada definida por$f$ y compárela con las tablas de las funciones en las partes a y b.
4. ¿Cuántas posibles funciones diferentes en tres variables$\left[B_2; \lor, \land, - \right]$ hay?

Ejercicio$\PageIndex{3}$

Dejar$[B; \lor , \land, - ]$ ser un álgebra booleana de orden 4, y dejar$f$ ser una función booleana de dos variables en$B\text{.}$

1. ¿Cuántos elementos hay en el dominio de f?
2. ¿Cuántas funciones booleanas diferentes hay de dos, variables? ¿Tres variables?
3. Determinar la forma normal minterm de$f\left(x_1, x_2\right)=x_1\lor x_2\text{.}$
4. Si$B=\{0, a, b, 1\}\text{,}$ define una función desde$B^2$ dentro$B$ que no es una función booleana.

Responder

1. El número de elementos en el dominio de$f$ es$16=4^{2}=|B|^{2}$
2. Con dos variables, hay$4^{3}=256$ diferentes funciones booleanas. Con tres variables, existen$4^{8}=65536$ diferentes funciones booleanas.
3. $f(x_{1},\:x_{2})=(1∧\overline{x_1}∧\overline{x_2})∨(1∧\overline{x_1}∧\overline{x_2})∨(1∧x1∧\overline{x_2})∨(0∧x1∧x2)$
4. Considerar$f:B^{2}→B$, definido por$f(0,0)=0$$f(0,1)=1$,$f(1,0)=a$,$f(1,1)=a$,$f(0,a)=b$, y, con las imágenes de todos los demás pares$B^{2}$ definidos arbitrariamente. Esta función no es una función booleana. Si asumimos que es función booleana entonces se$f$ puede calcular con una expresión booleana$M(x_1,x_2)$. Esta expresión se puede poner en forma normal minterm:
   $$M(x_1,x_2)=(c_1∧\overline{x_1}∧\overline{x_2})∨(c_2∧\overline{x_1}∧x_2)∨(c_3∧x_1∧\overline{x_2})∨(c_4∧x_1∧x_2)\nonumber$$
   $$\begin{aligned}f(0,0)&=0⇒M(0,0)=0⇒c_1=0 \\ f(0,1)&=1⇒M(0,0)=1⇒c_2=1 \\ f(1,0)&=a⇒M(0,0)=a⇒c_3=a \\ f(1,1)&=a⇒M(0,0)=a⇒c_4=a\end{aligned}$$
   Por lo tanto,$M(x_1,x_2)=(\overline{x_1}∧x_2)∨(a∧x_1∧\overline{x_2})∨(a∧x_1∧x_2)$ y así, usando esta fórmula,$M(0,a)=(\overline{0}∧a)∨(a∧0∧\overline{a})∨(a∧0∧a)=a$ Esto contradice$f(0,a)=b$, y así no$f$ es una función booleana.