14.3: Autómatas, Máquinas de Estado Finito

Última actualización
Guardar como PDF

Page ID: 117134

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección, presentaremos el concepto de una máquina abstracta. Las máquinas que examinaremos serán (en teoría) capaces de realizar muchas de las tareas asociadas a las computadoras digitales. Una de esas tareas es resolver el problema de reconocimiento para un idioma. Nos concentraremos en una clase de máquinas, máquinas de estado finito (autómatas finitos). Y veremos que son precisamente las máquinas que son capaces de reconocer cuerdas en una gramática regular.

Dado un alfabeto$X\text{,}$ imaginaremos una cadena en$X^*$ para ser codificada en una cinta que llamaremos cinta de entrada. Cuando nos referimos a una cinta, podríamos imaginar una tira de material que se divide en segmentos, cada uno de los cuales puede contener ya sea una letra o un espacio en blanco.

La máquina abstracta típica incluye un dispositivo de entrada, el cabezal de lectura, que es capaz de leer el símbolo del segmento de la cinta de entrada que se encuentra actualmente en la cabeza de lectura. Algunas máquinas más avanzadas tienen un cabezal de lectura/escritura que también puede escribir símbolos en la cinta. El movimiento de la cinta de entrada después de leer un símbolo depende de la máquina. Con una máquina de estado finito, el siguiente segmento de la cinta de entrada siempre se mueve al cabezal de lectura después de que se haya leído un símbolo. La mayoría de las máquinas (incluidas las máquinas de estado finito) también tienen una cinta de salida separada que se escribe con un cabezal de escritura. Los símbolos de salida provienen de un alfabeto de salida,$Z\text{,}$ que puede o no ser igual al alfabeto de entrada. El componente más significativo de una máquina abstracta es su estructura de memoria. Esta estructura puede variar desde un número finito de bits de memoria (como en una máquina de estado finito) hasta una cantidad infinita de memoria que se puede almacenar en forma de una cinta que se puede leer y escribir en (como en una máquina Turing).

Definición $\PageIndex{1}$: Finite-State Machine

Una máquina de estado finito es definida por un quinteto$(S, X, Z, w, t)$ donde

$S=\{s_1, s_2,\ldots , s_r\}$es el conjunto de estados, un conjunto finito que corresponde al conjunto de configuraciones de memoria que la máquina puede tener en cualquier momento.
$X=\{x_1, x_2, \ldots ,x_m\}$es el alfabeto de entrada.
$Z=\{z_1,z_2, \ldots ,z_n\}$es el alfabeto de salida.
$w: X\times S \to Z$es la función de salida, que especifica qué símbolo de salida$w(x, s) \in Z$ se escribe en la cinta de salida cuando la máquina está en estado$s$ y$x$ se lee el símbolo de entrada.
$t:X\times S\to S$es la función de siguiente estado (o transición), que especifica qué estado debe ingresar$t(x, s) \in S$ la máquina cuando está en estado$s$ y lee el símbolo$x\text{.}$

Ejemplo$\PageIndex{1}$: Vending Machine as a Finite-State Machine

Muchos dispositivos mecánicos, como las máquinas expendedoras simples, pueden considerarse máquinas de estado finito. Para simplificar, suponga que una máquina expendedora dispensa paquetes de chicle, menta verde (S), menta (P) y burbuja (B), por$25$ centavos cada uno. Podemos definir el alfabeto de entrada para ser

\ begin {ecuación*}\ {\ textrm {depósito 25 centavos},\ textrm {presione S},\ textrm {presione P},\ textrm {presione B}\}\ final {ecuación*}

y el estado establecido para ser$\{\textrm{Locked}, \textrm{ Select}\}\text{,}$ donde el depósito de un cuarto desbloquea el mecanismo de liberación de la máquina y le permite seleccionar un sabor de chicle. Dejaremos al lector imaginar cuál sería el alfabeto de salida, la función de salida y la función de siguiente estado. También estás invitado a dejar volar tu imaginación e incluir características como una palanca de devolución de monedas y un creador de cambios.

Ejemplo$\PageIndex{2}$: A Parity Checking Machine

La siguiente máquina se llama verificador de paridad. Reconoce si una cadena$B^*$ contiene o no un número par de 1s. La estructura de memoria de esta máquina refleja el hecho de que para verificar la paridad de una cadena, solo necesitamos hacer un seguimiento de si se ha detectado un número impar o par de 1's.

El alfabeto de entrada es$B=\{0,1\}$ y el alfabeto de salida también es$B\text{.}$ El conjunto de estados es$\{even, odd\}\text{.}$ La siguiente tabla define las funciones de salida y siguiente estado.

\ begin {ecuation*}\ begin {array} {c|ccc} x & s & w (x, s) & t (x, s)\\ hline\ begin {array} {c} 0\\ 0\\ 1\\ 1\\ end {array} &\ begin {array} {c}\ textrm {par}\\ textrm {impar}\\ textrm m {par}\\\ textrm {impar}\\\ end {array} &\ begin {array} {c} 0\\ 1\\ 1\\ 0\\ final {array} &\ begin {array} { c}\ textrm {par}\\\ textrm {impar}\\ textrm {impar}\\\ textrm {par}\\\ final {matriz}\\ final {matriz}\ final {ecuación*}

Observe cómo el valor de la salida más reciente en cualquier momento es una indicación del estado actual de la máquina. Por lo tanto, si empezamos en el estado par y leemos cualquier cinta de entrada finita, la última salida corresponde al estado final del verificador de paridad y nos dice la paridad de la cadena en la cinta de entrada. Por ejemplo, si la cadena 11001010 se lee de izquierda a derecha, la cinta de salida, también de izquierda a derecha, será 10001100. Dado que el último carácter es un 0, sabemos que la cadena de entrada tiene paridad par.

Un método alternativo para definir una máquina de estado finito es con un diagrama de transición. Un diagrama de transición es un gráfico dirigido que contiene un nodo para cada estado y bordes que indican las funciones de transición y salida. Un borde$\left(s_i,s_j\right)$ que está etiquetado$x/z$ indica que en estado$s_i$ la entrada$x$ da como resultado una salida de$z$ y el siguiente estado es$s_j\text{.}$ Eso es,$w\left(x, s_i\right)=z$ y$t\left(x, s_i\right)=s_j\text{.}$ El diagrama de transición para el verificador de paridad aparece en la Figura$\PageIndex{1}$. En ejemplos posteriores, veremos que si hay diferentes entradas,$x_i$ y$x_j\text{,}$ mientras en el mismo estado dando como resultado las mismas transiciones y salidas, etiquetamos un solo borde$x_i, \left.x_j\right/z$ en lugar de dibujar dos aristas con etiquetas$\left.x_i\right/z$ y$\left.x_j\right/z\text{.}$

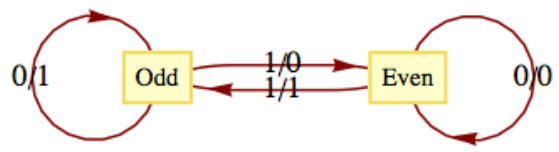$clipboard_e0991f49dc7347c56809b6367d973606b.png$ Figura$\PageIndex{1}$: Diagrama de transición para un verificador de paridad

Una de las características más significativas de una máquina de estado finito es que no conserva información sobre sus estados pasados a la que pueda acceder la propia máquina. Por ejemplo, después de introducir una cinta codificada con los símbolos 01101010 en el verificador de paridad, el estado actual será parejo, pero no tenemos indicación dentro de la máquina si siempre ha estado o no en estado par. Observe cómo la cinta de salida no se considera parte de la memoria de la máquina. En este caso, la cinta de salida sí contiene un “historial” de los estados pasados del verificador de paridad. Suponemos que la máquina de estado finito no tiene forma de recuperar la secuencia de salida para su uso posterior.

Ejemplo$\PageIndex{3}$: A Baseball Machine

Considera la siguiente versión simplificada del juego de beisbol. Para ser precisos, esta máquina describe una media entrada de un juego de béisbol simplificado. Supongamos que además del plato casero, solo hay una base en lugar de las tres bases habituales. Además, supongamos que solo hay dos outs por entrada en lugar de los tres habituales. Nuestro alfabeto de entrada consistirá en los tipos de hits que el bateador podría tener: out (O), double play (DP), single (S) y jonrón (HR). El DP de entrada está destinado a representar una bola bateada que resultaría en una jugada doble (dos outs), si es posible. El DP de entrada puede ocurrir entonces en cualquier momento. El alfabeto de salida son los números 0, 1 y 2 para el número de corridas que se pueden puntuar como resultado de cualquier entrada. El conjunto de estados contiene la situación actual en la entrada, el número de outs y si un corredor base se encuentra actualmente en la base. La lista de estados posibles es entonces 00 (para 0 outs y 0 corredores), 01, 10, 11, y end (cuando termina la media entrada). El diagrama de transición para esta máquina aparece en la Figura$\PageIndex{2}$

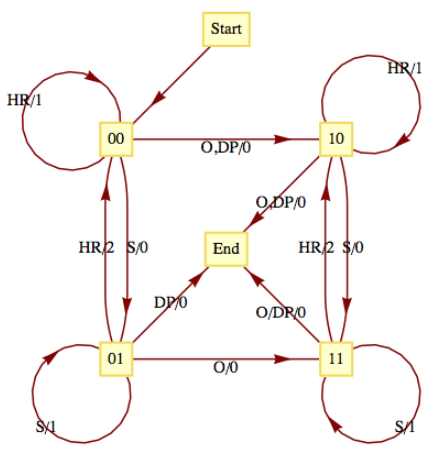$clipboard_eeb5b88cb75c15c28de9531229be2ecd3.png$ Figura$\PageIndex{2}$: Diagrama de transición para un juego simplificado de béisbol

Concentrémonos en un solo estado. Si el estado actual es 01, 0 outs y 1 corredor en base, cada entrada da como resultado una combinación diferente de salida y siguiente estado. Si el bateador golpea mal la pelota (una jugada doble) la salida es cero carreras y la entrada ha terminado (se ha hecho el límite de dos outs). Una salida simple también da como resultado una salida de 0 corridas y el siguiente estado es 11, una salida y un corredor en la base. Si el bateador golpea una sola, una carrera anota (salida = 1) mientras el estado permanece 01. Si se golpea un jonrón, se anotan dos carreras (salida = 2) y el siguiente estado es 00. Si hubiéramos permitido tres outs por entrada, esta gráfica sólo sería marginalmente más complicada. El juego habitual con tres bases sería un poco más complicado, sin embargo.

Ejemplo$\PageIndex{4}$: Recognition in Regular Languages

Como mencionamos al inicio de esta sección, las máquinas de estado finito pueden reconocer cadenas en un lenguaje regular. Considera el lenguaje$L$ sobre$\{a,b,c\}$ que contiene las cadenas de longitud positiva en las que cada una$a$ es seguida por$b$ y cada una$b$ es seguida por$c\text{.}$ Una de esas cadenas es$bccabcbc\text{.}$ Este lenguaje es regular. Una gramática para el lenguaje serían símbolos no terminales$\{A,B,C\}$ con símbolo inicial$C$ y reglas de producción$A\to bB\text{,}$$B\to cC\text{,}$$C\to aA\text{,}$$C\to bB\text{,}$$C \to cC\text{,}$$C \to c\text{.}$ Una máquina de estado finito (Figura$\PageIndex{3}$) que reconoce este lenguaje se puede construir con un estado para cada símbolo no terminal y un estado adicional (Rechazar) que se ingresa si tiene lugar alguna producción no válida. Al final de una cinta de entrada que codifica una cadena en$\{a,b,c\}^*\text{,}$ sabremos a cuándo pertenece la cadena en$L$ base a la salida final. Si la salida final es 1, la cadena pertenece a$L$ y si es 0, la cadena no pertenece a$L\text{.}$ Además, el reconocimiento se puede lograr examinando el estado final de la máquina. La cadena de entrada pertenece al idioma si y solo si el estado final es$C\text{.}$

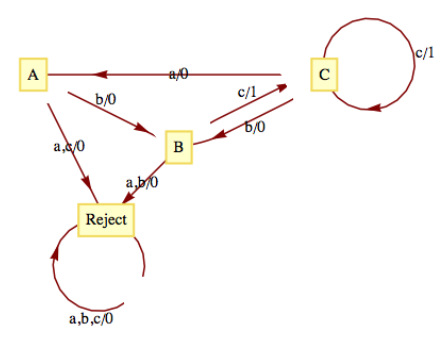$clipboard_ec7fa3b24da05ad62b647b5bc7db0e375.png$ Figura$\PageIndex{3}$

La construcción de esta máquina es bastante fácil: observe cómo cada regla de producción se traduce en un borde entre estados distintos de Rechazar. Por ejemplo,$C\to bB$ indica que en Estado$C\text{,}$ una entrada de$b$ coloca la máquina en Estado$B\text{.}$ No todos los conjuntos de reglas de producción pueden traducirse tan fácilmente a una máquina de estado finito. Otro conjunto de reglas de producción para$L$ is$A\to aB\text{,}$$B\to bC\text{,}$$C\to cA\text{,}$$C\to cB\text{,}$$C\to cC$ y$C\to c\text{.}$ Técnicas para construir máquinas de estado finito a partir de reglas de producción no es nuestro objetivo aquí. De ahí que solo esperemos que experimentes con las reglas de producción hasta que se encuentren las apropiadas.

Ejemplo $\PageIndex{5}$: A Binary Adder

Se puede diseñar una máquina de estado finito para agregar enteros positivos de cualquier tamaño. Dados dos enteros en forma binaria,$a=a_na_{n-1} \cdots a_1a_0$ y$b=b_n b_{n-1}\cdots b_1b_0\text{,}$ la máquina toma como secuencia de entrada los bits correspondientes de$a$ y$b$ leyendo de derecha a izquierda con un “bit de paridad” agregado

\ begin {ecuación*} a_0b_0\ izquierda (a_0+_2b_0\ derecha), a_1b_1\ izquierda (a_1+_2b_1\ derecha)\ ldots, a_nb_n\ izquierda (a_n+_2b_n\ derecha) ,111\ end {ecuación*}

Observe la entrada especial 111 al final. Todas las entradas posibles excepto la última deben igualar la paridad (contener un número par de unos). La secuencia de salida es la suma de$a$ y$b\text{,}$ comenzando con el dígito de las unidades, y proviene del conjunto$\{0,1,\lambda \}\text{.}$ El diagrama de transición para esta máquina aparece en la Figura$\PageIndex{4}$.

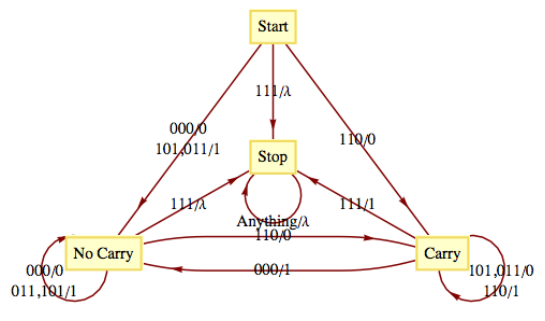$clipboard_e7363755635dcf9b6166d2a5f8c4372b1.png$ Figura$\PageIndex{4}$: Diagrama de transición para un sumador binario

14.3.1: Ejercicios

Ejercicio$\PageIndex{1}$

Dibuje un diagrama de transición para la máquina expendedora descrita en Ejemplo$\PageIndex{1}$.

Contestar: \ begin {equation*}\ begin {array} {cccc} x & s & Z (x, s) & t (x, s)\\ textrm {Depositar} 25\ not {c} &\ textrm {Bloqueado} &\ textrm {Nada} &\ textrm {Seleccionar}\\ textrm {Depositar} 25\ not {c} &\ textrm {Seleccionar} &\ textrm {Devolución} 25\ not {c} &\ textrm {Seleccionar}\\\ textrm {Presione} S &\ textrm {Bloqueado} &\ textrm {Nada} &\ textrm {Bloqueado}\\ textrm {Prensa} S &\ textrm {Seleccionar} &\ textrm {Dispensar} S &\ textrm {Bloqueado}\\ textrm {Presione} P &\ textrm {Bloqueado} &\ textrm {Nada} &\ textrm {Bloqueado}\\ textrm {Presione} P &\ textrm {Seleccionar} &\ textrm { Dispensar} P &\ textrm {Bloqueado}\\\ textrm {Prensa} B &\ textrm {Bloqueado} &\ textrm {Nada} &\ textrm {Bloqueado}\\ textrm {Prensa} B &\ textrm {Seleccionar} &\ textrm {Dispensar} B &\ textrm {Bloqueado}\\ textrm {Bloqueado}\\ textrm {Bloqueado}\\ textrm {Presione} B &\ textrm {Bloqueado}\\ textr*}

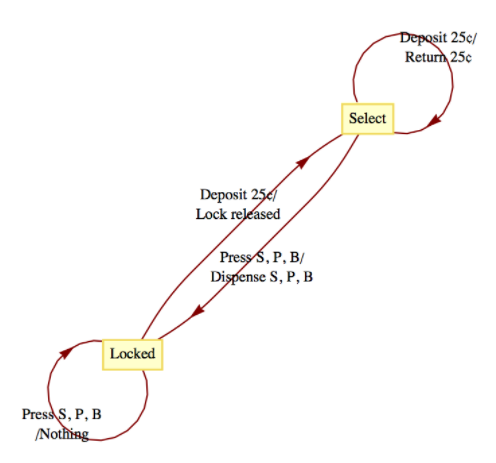$clipboard_e5de5b8ea7cb4dc914ded7eea61da8495.png$ Figura$\PageIndex{5}$: Transiciones de máquina expendedora

Ejercicio$\PageIndex{2}$

Construya máquinas de estado finito que reconozcan los idiomas regulares que identificó en la Sección 14.2.

Ejercicio$\PageIndex{3}$

¿Cuál es el conjunto de entrada para la máquina de adición binaria en Example$\PageIndex{5}$?

Contestar: $\{000, 011, 101, 110, 111\}$

Ejercicio$\PageIndex{4}$

¿Qué secuencia de entrada se utilizaría para calcular la suma de 1101 y 0111 (enteros binarios)? ¿Cuál sería la secuencia de salida?

Ejercicio$\PageIndex{5}$

El Decodificador de Código Gris. La máquina de estado finito definida por la siguiente figura tiene una interesante conexión con el Código Gris.

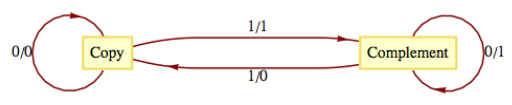$clipboard_eda31e092b76d26ebf41e3745d4153101.png$ Figura$\PageIndex{6}$: Decodificador de código gris

Dada una cadena$x=x_1x_2\cdots x_n\in B^n\text{,}$ podemos preguntar dónde$x$ aparece en el estado$G_n\text{.}$ Comenzando en Copiar, la cadena de entrada$x$ dará como resultado una cadena de salida$z\in B^n\text{,}$ que es la forma binaria de la posición de$x$ en$G_n\text{.}$ Recall que las posiciones están numeradas de 0 a$2^n-1\text{.}$

¿En qué posiciones$(0-31)$ aparecen 10110, 00100 y 11111 en$G_5\text{?}$
Demostrar que el Decodificador de Código Gris siempre funciona.

Contestar

- Entrada: 10110, Salida: 11011$\Rightarrow$ 10110 está en la posición 27
- Entrada: 00100, Salida: 00111$\Rightarrow$ 00100 está en la posición 7
- Entrada:11111, Salida: 10101$\Rightarrow$ 11111 está en la posición 21
Vamos$x=x_1x_2\ldots x_n$ y recordemos que para$n\geq 1\text{,}$$G_{n+1}=\left( \begin{array}{c} 0G_n \\ 1G_n^r \\ \end{array} \right)\text{,}$ donde$G_n^r$ esta el reverso de$G_n\text{.}$ Para probar que el Decodificador de Código Gris siempre funciona, deja$p(n)$ ser la proposición “Comenzando en estado Copy,$x$'s output es la posición de$x$ in$G_n\text{;}$ e iniciando en Complemento state,$x$'s output es la posición de$x$ in$G_n^r\text{.}$” Que p (1) sea verdadero es fácil de verificar para ambos valores posibles de$x\text{,}$ 0 y 1. Ahora supongamos que para algunos$n\geq 1\text{,}$$p(n)$ es verdadero y considera que$x_1=0\text{,}$$x$ la salida de$x=x_1x_2\ldots x_nx_{n+1}\text{.}$
If es un cero seguido de la salida para$\left(x_2\ldots x_nx_{n+1}\right)$ comenzar en estado Copy. Por la hipótesis de inducción, esto es cero seguido de la posición de$\left(x_2 \ldots x_n x_{n+1}\right)$ en la$G_n\text{,}$ que está la posición de$x$ in$G_{n+1}\text{,}$ por la definición de salida$x_1=1\text{,}$$x$ de$G\text{.}$
If es una seguida por la salida para$\left(x_2\ldots x_nx_{n+1}\right)$ comenzar en Estado del complemento. Por la hipótesis de inducción, esta es una seguida de la posición de$\left(x_2\ldots x_nx_{n+1}\right)$ en la$G_n^r\text{,}$ que está la posición de$x$ in$G_{n+1}\text{,}$ por la definición de$G\text{.}$$\square$