14.2: Monoides libres e idiomas

En esta sección, introduciremos el concepto de un lenguaje. Los idiomas son subconjuntos de cierto tipo de monoide, el monoide libre sobre un alfabeto. Después de definir un monoide libre, discutiremos los idiomas y algunos de los problemas básicos relacionados con ellos. También discutiremos las formas comunes en que se definen las lenguas.

$A$Sea un conjunto no vacío, al que llamaremos alfabeto. Nuestro interés primordial estará en el caso donde$A$ sea finito; sin embargo,$A$ podría ser infinito para la mayoría de las situaciones que vamos a describir. Los elementos de$A$ se llaman letras o símbolos. Entre los alfabetos que usaremos están$B=\{0,1\}\text{,}$ y el conjunto de caracteres ASCII (American Standard Code for Information Interchange), que simbolizamos como$ASCII\text{.}$

Definición $\PageIndex{1}$: Strings over an Alphabet

Una cadena de longitud$n\text{,}$$n \geqslant 1$ sobre el alfabeto$A$ es una secuencia de$n$ letras de$A\text{:}$$a_1a_2\ldots a_n\text{.}$ La cadena nula,$\lambda\text{,}$ se define como la cadena de longitud cero que no contiene letras. El conjunto de cadenas de longitud$n$ sobre$A$ se denota por$A^n\text{.}$ El conjunto de todas las cadenas sobre$A$ se denota$A^*\text{.}$

Nota$\PageIndex{1}$

1. Si la longitud de la cadena$s$ es$n\text{,}$ escribimos$\lvert s \rvert =n\text{.}$
2. La cadena nula no es lo mismo que el conjunto vacío, aunque son similares en muchos sentidos. $A^0 = \{\lambda\}\text{.}$
3. $A^*=A^0\cup A^1\cup A^2\cup A^3\cup \cdots \textrm{ and if } i\neq j,A^i\cap A^j=\emptyset\text{;}$es decir,$\{A^0,A^1,A^2,A^3,\ldots \}$ es una partición de$A^*\text{.}$
4. Un elemento de$A$ puede aparecer cualquier número de veces en una cadena.

Teorema$\PageIndex{1}$

Si$A$ es contable, entonces$A^*$ es contable.

Prueba

Caso 1. Dado el alfabeto$B=\{0,1\}\text{,}$ podemos definir una biyección de los enteros positivos a$B^*\text{.}$ Cada entero positivo tiene una expansión binaria$d_kd_{k-1}\cdots d_1d_0\text{,}$ donde cada uno$d_j$ es 0 o 1 y$d_k=1\text{.}$ Si$n$ tiene tal expansión binaria, entonces$2^k \leq n\leq 2^{k+1}\text{.}$ Definimos$f:\mathbb{P}\to B^*$ por$f(n)=f\left(d_kd_{k-1}\cdots d_1d_0\right)=d_{k-1}\cdots d_1d_0,$ donde $f(1)=\lambda\text{.}$Cada una de las$2^k$ cadenas de longitud$k$ son las imágenes de exactamente uno de los enteros entre$2^k\textrm{ and } 2^{k+1}-1.$ De su definición,$f$ es claramente una biyección; por lo tanto,$B^*$ es contable.

Caso 2:$A$ es finito. Describiremos cómo se maneja este caso con un ejemplo primero y luego daremos la prueba general. Si$A=\{a,b,c,d,e\}\text{,}$ entonces podemos codificar las letras$A$ en cadenas de$B^3\text{.}$ Uno de los esquemas de codificación (hay muchos) es$a\leftrightarrow 000, b\leftrightarrow 001, c\leftrightarrow 010, d\leftrightarrow 011, \textrm{ and } e\leftrightarrow 100\text{.}$ Ahora cada cadena en$A^*$ corresponde a una cadena diferente en por$B^*\text{;}$ ejemplo,$ace\text{.}$ correspondería con$000010100\text{.}$ La cardinalidad de $A^*$es igual a la cardinalidad del conjunto de cadenas que se pueden obtener de este sistema de codificación. Las posibles cadenas codificadas deben ser contables, ya que son un subconjunto de un conjunto contable,$B^*\text{.}$ Por lo tanto,$A^*$ es contable.

Si$\lvert A\rvert =m\text{,}$ entonces las letras en se$A$ pueden codificar usando un conjunto de cadenas de longitud fija de$B^*\text{.}$ Si$2^{k-1} < m \leq 2^k\text{,}$ entonces hay al menos tantas cadenas de longitud$k$ en$B^k$ como hay letras en$A\text{.}$ Ahora podemos asociar cada letra$A$ con con una diferente elemento de$B^k\text{.}$ Entonces cualquier cadena en$A^*\text{.}$ corresponde a una cadena en$B^*\text{.}$ Por el mismo razonamiento que en el ejemplo anterior,$A^*$ es contable.

Caso 3:$A$ es Contable Infinito. Dejaremos este caso como ejercicio.

Definición $\PageIndex{2}$: Concatenation

Let$a=a_1a_2\cdots a_m$ y$b=b_1b_2\cdots b_n$ ser cadenas de longitud$m$ y$n\text{,}$ respectivamente. La concatenación de$a$ con$b\text{,}$$a+b\text{,}$ es la cadena$a_1a_2\cdots a_mb_1b_2\cdots b_n$ de longitud$m+n\text{.}$

Existen varios símbolos que se utilizan para la concatenación. Elegimos usar el que también se usa en Python y SameMath.

view sourceprint?

1	'good'+'bye'

El conjunto de cadenas sobre cualquier alfabeto es un monoide bajo concatenación.

Nota$\PageIndex{2}$

1. La cadena nula es el elemento de identidad de$[A^*; +]\text{.}$ De ahora en adelante, denotaremos el monoide de cadenas sobre$A$ por$A^*\text{.}$
2. La concatenación no es conmutativa, siempre y cuando$\lvert A\rvert > 1\text{.}$
3. Si$\lvert A_1 \rvert = \lvert A_2 \rvert\text{,}$ entonces los monoides$A_1^*$ y$A_2^*$ son isomórficos. Un isomorfismo se puede definir usando cualquier bijección$f:A_1\to A_2\text{.}$ Si$a=a_1a_2\cdots a_n \in A_1^*\text{,}$$f^*(a)=(f(a_1)f(a_2)\cdots f(a_n))$ define una bijección desde$A_1^*$ dentro$A_2^*\text{.}$ Dejaremos que el lector lo demuestre para todos$a,b,\in A_1^*,f^*(a+b)=f^*(a)+f^*(b)\text{.}$

A los idiomas del mundo, el inglés, el alemán, el ruso, el chino, etc., se les llama lenguas naturales. Para poder comunicarte por escrito en cualquiera de ellos, primero debes conocer las letras del alfabeto y luego saber combinar las letras de manera significativa. Un lenguaje formal es una abstracción de esta situación.

Definición$\PageIndex{3}$: Formal Language

Si$A$ es un alfabeto, un lenguaje formal sobre$A$ es un subconjunto de$A^*\text{.}$

Ejemplo$\PageIndex{1}$: Some Formal Languages

1. El inglés se puede considerar como un idioma sobre letras$A,B,\cdots Z\text{,}$ tanto mayúsculas como minúsculas, y otros símbolos especiales, como los signos de puntuación y el espacio en blanco. Exactamente qué subconjunto de las cadenas sobre este alfabeto define el idioma inglés es difícil de precisar exactamente. Esta es una característica de las lenguas naturales que tratamos de evitar con las lenguas formales.
2. El conjunto de todos los archivos de flujo ASCII se puede definir en términos de un lenguaje sobre ASCII. Un archivo de flujo ASCII es una secuencia de cero o más líneas seguidas de un símbolo de fin de archivo. Una línea se define como una secuencia de caracteres ASCII que termina con el carácter a “nueva línea”. El símbolo de fin de archivo depende del sistema.
3. El conjunto de todas las expresiones sintácticamente correctas en cualquier lenguaje de computadora es un lenguaje sobre el conjunto de cadenas ASCII.
4. Algunos idiomas más$B$ son
   • $\displaystyle L_1=\{s\in B^* \mid s \textrm{ has exactly as many 1's as it has 0's}\}$
   • $\displaystyle L_2=\{1+s+0 \mid s\in B^*\}$
   • $L_3=\langle 0,01\rangle$= el submonoide de$B^*$ generado por$\{0,01\}\text{.}$

Investigación$\PageIndex{1}$: Two Fundamental Problems: Recognition and Generation

Los problemas de generación y reconocimiento son básicos para la programación informática. Dado un lenguaje,$L\text{,}$ el programador debe saber escribir (o generar) un programa sintácticamente correcto que resuelva un problema. Por otro lado, el compilador debe ser escrito para reconocer si un programa contiene algún error de sintaxis.

Problema$\PageIndex{1}$: The Recognition Problem

Dado un lenguaje formal sobre$A\text{,}$ el alfabeto, el Problema de Reconocimiento es diseñar un algoritmo que determine la verdad de$s\in L$ en un número finito de pasos para todos$s\in A^*\text{.}$ Cualquier algoritmo de este tipo se denomina algoritmo de reconocimiento.

Definición$\PageIndex{4}$: Recursive Language

Un lenguaje es recursivo si existe un algoritmo de reconocimiento para ello.

Ejemplo$\PageIndex{2}$: Some Recursive Languages

1. El lenguaje de proposiciones sintácticamente correctas sobre conjunto de expresiones de variables proposicionales es recursivo.
2. Los tres idiomas en 7 (d) son todos recursivos. Algoritmos de reconocimiento para$L_1$ y$L_2$ deberían ser fáciles de imaginar. La razón por la que un algoritmo de reconocimiento$L_3$ podría no ser obvia es que la definición de$L_3$ es más críptica. No nos dice a qué pertenece$L_3\text{,}$ justo lo que se puede usar para crear cadenas en$L_3\text{.}$ Esta es la cantidad de idiomas que se definen. Con una segunda descripción de$L_3\text{,}$ podemos diseñar fácilmente un algoritmo de reconocimiento. Puedes probar que
   \ begin {ecuation*} L_3=\ {s\ in B^*\ mid s=\ lambda\ textrm {o} s\ textrm {comienza con un 0 y no tiene 1's consecutivos}\}\ text {.} \ end {ecuación*}

Problema$\PageIndex{2}$: The Generation Problem

Diseñar un algoritmo que genere o produzca cualquier cadena en$L\text{.}$ Aquí presumimos que$A$ es finito o contablemente infinito; por lo tanto,$A^*$ es contable por Teorema$\PageIndex{1}$, y$L \subseteq A^*$ debe ser contable. Por lo tanto, la generación de$L$ cantidades para crear una lista de cadenas en$L\text{.}$ La lista puede ser finita o infinita, y debe poder mostrar que cada cadena en$L$ aparece en algún lugar de la lista.

Teorema$\PageIndex{2}$: Recursive Implies Generating

1. Si$A$ es contable, entonces existe un algoritmo de generación para$A^*\text{.}$
2. Si$L$ es un lenguaje recursivo sobre un alfabeto contable, entonces existe un algoritmo generador para$L\text{.}$

Prueba

La parte (a) se desprende del hecho de que$A^*$ es contable; por lo tanto, existe una lista completa de cadenas en$A^*\text{.}$

Para generar todas las cadenas de$L\text{,}$ inicio con una lista de todas las cadenas en$A^*$ y una lista vacía,$W\text{,}$ de cadenas en$L\text{.}$ Para cada cadena$s\text{,}$ usa un algoritmo de reconocimiento (existe uno ya que$L$ es recursivo) para determinar si$s\in L\text{.}$ si se$s \in L\text{,}$ agrega a$W\text{;}$ de lo contrario “tíralo”. Luego ve a la siguiente cadena en la lista de$A^*\text{.}$

Ejemplo$\PageIndex{3}$

Dado que todos los lenguajes en 7 (d) son recursivos, deben tener algoritmos generadores. El que se da en la prueba del Teorema no$\PageIndex{2}$ suele ser el más eficiente. Probablemente podrías diseñar algoritmos de generación más eficientes para$L_2$ y$L_3\text{;}$ sin embargo, un mejor algoritmo generador para no$L_1$ es tan obvio.

Los problemas de reconocimiento y generación pueden variar en dificultad dependiendo de cómo se defina un lenguaje y qué tipo de algoritmos nos permitimos utilizar. Esto no quiere decir que el medio por el que se define un lenguaje determine si es recursivo. Simplemente significa que la verdad de la afirmación “$L$es recursiva” puede ser más difícil de determinar con una definición que con otra. Cerraremos esta sección con una discusión de gramáticas, que son formas estándar de definición para un lenguaje. Cuando nos limitamos a solo ciertos tipos de algoritmos, podemos afectar nuestra capacidad para determinar si$s\in L$ es cierto. Al definir un lenguaje recursivo, no nos restringimos de ninguna manera en lo que respecta al tipo de algoritmo que se utilizará. En la siguiente sección, consideraremos máquinas llamadas autómatas finitas, que sólo pueden realizar algoritmos simples.

Una forma común de definir un idioma es por medio de una estructura de frases gramática (o gramática, para abreviar). El conjunto de cadenas que se pueden producir usando un conjunto de reglas gramaticales se llama lenguaje de estructura de frases.

Ejemplo$\PageIndex{4}$: Zeros Before Ones

Podemos definir el conjunto de todas las cadenas sobre$B$ las cuales todos los 0 preceden a todos los 1 de la siguiente manera. Define el símbolo de inicio$S$ y establezca reglas que$S$ puedan ser reemplazadas por cualquiera de las siguientes:$\lambda\text{,}$$0S\text{,}$ o$S1\text{.}$ Estas reglas de reemplazo generalmente se denominan reglas de producción. Por lo general se escriben en el formato$S\to \lambda\text{,}$$S\to 0S\text{,}$ y$S\to S1\text{.}$ ahora definen$L$ como el conjunto de todas las cadenas que se pueden producir comenzando con$S$ y aplicando las reglas de producción hasta que ya$S$ no aparezca. Las cuerdas en$L$ son exactamente las que se describen anteriormente.

Definición $\PageIndex{5}$: Phase Structure Grammar

Una gramática de estructura de frases consta de cuatro componentes:

1. Un conjunto finito no vacío de caracteres terminales,$T\text{.}$ Si la gramática está definiendo un idioma sobre$A\text{,}$$T$ es un subconjunto de$A^*\text{.}$
2. Un conjunto finito de caracteres no terminales,$N\text{.}$
3. Un símbolo de partida,$S\in N\text{.}$
4. Un conjunto finito de reglas de producción, cada una de la forma$X\to Y\text{,}$ donde$X$ y$Y$ son cadenas sobre$A\cup N$ tal que$X\neq Y$ y$X$ contiene al menos un símbolo no terminal.

Si$G$ es una gramática de estructura de frases,$L(G)$ es el conjunto de cadenas que se pueden producir comenzando con$S$ y aplicando las reglas de producción un número finito de veces hasta que no queden caracteres no terminales. Si un lenguaje puede ser definido por una gramática de estructura de frases, entonces se llama lenguaje de estructura de frases.

Ejemplo$\PageIndex{5}$: Alternating Bits Language

El lenguaje$B$ que consiste en cadenas alternas de 0 y 1 es un lenguaje de estructura de frases. Se puede definir por la siguiente gramática:

1. Caracteres terminales:$\lambda\text{,}$$0\text{,}$ y$1$
2. Caracteres no terminales:$S\text{,}$$T\text{,}$ y$U$
3. Símbolo inicial:$S$
4. Reglas de producción:
   \ begin {ecuation*}\ begin {array} {ccc} S\ a T & S\ a U & S\ a\ lambda\\ S\ a 0& & S\ a 1\\ S\ a 0T&& S\ a 1U\\ T\ a 10T&& T\ a 10\\ U\ a 01U& & U\ a 01\\ end {array} end\ {ecuación*}

Estas reglas se pueden visualizar con una gráfica:

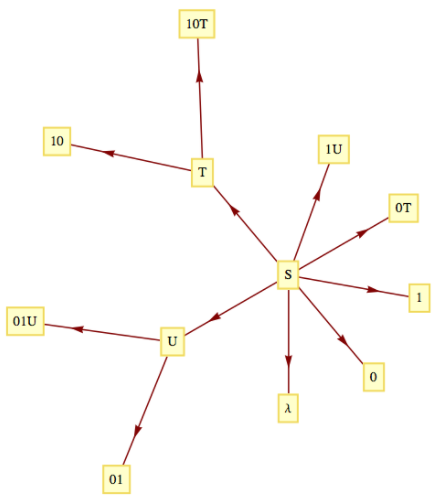Figura$\PageIndex{1}$: Reglas de producción para el lenguaje de alternar 0 y 1

Podemos verificar que una cadena como 10101 pertenece al idioma comenzando con$S$ y produciendo 10101 usando las reglas de producción un número finito de veces:$S\to 1U\to 101U\to 10101\text{.}$

Ejemplo$\PageIndex{6}$: Valid SageMath Variables

$G$Sea la gramática con componentes:

1. Símbolos terminales = todas las letras del alfabeto (tanto mayúsculas como minúsculas), dígitos del 0 al 9 y guión bajo
2. Símbolos no terminales:$\{I, X\}\text{,}$
3. Símbolo inicial:$I$
4. Reglas de producción:$I \to \alpha\text{,}$ donde$\alpha$ está cualquier letra,$I \to \alpha+X$ para cualquier letra$\alpha\text{,}$$X\to X+\beta$ para cualquier letra, dígito o guión bajo,$\beta\text{,}$ y$X \to \beta$ para cualquier letra, dígito o guión bajo,$\beta\text{.}$ Hay un total de reglas de$52+52+63+63=230$ producción para esta gramática. El idioma$L(G)$ consta de todos los nombres de variables SameMath válidos.

Ejemplo$\PageIndex{7}$: Backus-Naur Form

La forma Backus-Naur (BNF) es una forma alternativa popular de definir las reglas de producción en una gramática. Si las reglas de producción$A\to B_1, A\to B_2,\ldots A\to B_n$ son parte de una gramática, se escribirían en BNF como$A ::=B_1 \mid B_2\mid \cdots \mid B_n\text{.}$ El símbolo$\mid$ en BNF se lee como “o” mientras que el$::=$ se lee como “se define como”. Notaciones adicionales de BNF son que$\{x\}\text{,}$ representa cero o más repeticiones de$x$ y$[y]$ significa que$y$ es opcional.

Una versión BNF de las reglas de producción para una variable SameMath,$I\text{,}$ es

\ begin {ecuación*}\ begin {array} {l} letra: :=a\ mid b\ mid c\ mid\ cdots\ mid z\ mid A\ mid B\ mid B\ mid\ cdots\ mid Z\\ digit: :=0\ mid 1\ mid\ cdots\ mid 9\\ I: := letra\ {letra\ mid digit\ mid\ _\}\\ end {array}\ end {ecuación*}

Ejemplo$\PageIndex{8}$: The Language of Simple Arithmetic Expressions

Una expresión aritmética se puede definir en BNF. Por simplicidad, consideraremos solo expresiones obtenidas usando suma y multiplicación de enteros. Los símbolos terminales son (,), +, *, -, y los dígitos 0 a 9. Los símbolos no terminales son$E$ (para expresión),$T$ (término),$F$ (factor) y$N$ (número). El símbolo inicial es Las reglas$E\text{.}$ de producción son

\ begin {ecuation*}\ begin {array} {c} E\ text: :=E+T\ mid T\\ T: :=T * F\ mid F\\ F: := (E)\ mid N\\ N: := [-]\ textrm {dígito}\ {\ textrm {dígito}\\ textrm {dígito}\}\\\\ end {array}\ text {.} \ end {ecuación*}

Un tipo particularmente simple de gramática de estructura de frases es la gramática regular.

Definición$\PageIndex{6}$: Regular Grammar

Una gramática regular (forma derecha) es una gramática cuyas reglas de producción son todas de la forma$A\to t$ y$A\to tB\text{,}$ donde$A$ y$B$ son no terminales y$t$ es terminal. Una gramática de forma izquierda solo permite$A \to t$ y$A\to Bt\text{.}$ Un lenguaje que tiene una estructura de frase regular se llama lenguaje regular.

Ejemplo$\PageIndex{9}$

1. El conjunto de nombres de variables Sage es un lenguaje regular ya que la gramática por la que definimos el conjunto es una gramática regular.
2. El lenguaje de todas las cadenas para las que todos los 0 preceden a todos los 1 (Ejemplo$\PageIndex{4}$) es regular; sin embargo, la gramática por la que definimos este conjunto no es regular. ¿Puedes definir estas cadenas con una gramática regular?
3. El lenguaje de las expresiones aritméticas no es regular.

Ejercicios

Ejercicio$\PageIndex{1}$

1. Si se está diseñando una computadora para operar con un juego de caracteres de 350 símbolos, ¿cuántos bits deben reservarse para cada carácter? Supongamos que cada carácter utilizará el mismo número de bits.
2. Haz lo mismo para 3,500 símbolos.

Responder

1. Para un conjunto de caracteres de 350 símbolos, el número de bits necesarios para cada carácter es el más pequeño de$n$ tal manera que$2^n$ es mayor o igual a 350. Dado que se necesitan$2^9= 512 > 350 > 2^8\text{,}$ 9 bits,
2. $2^{12}=4096 >3500> 2^{11}\text{;}$por lo tanto, se necesitan 12 bits.

Ejercicio$\PageIndex{2}$

Se señaló en el texto que la cadena nula y el conjunto nulo son diferentes. El primero es una cadena y el segundo es un conjunto, dos tipos diferentes de objetos. Discutir cómo los dos son similares.

Ejercicio$\PageIndex{3}$

¿Qué conjuntos de cadenas están definidos por la siguiente gramática?

1. Símbolos terminales:$\lambda$, 0 y 1
2. Símbolos no terminales:$S$ y$E$
3. Símbolo inicial:$S$
4. Reglas de producción:$S\to 0S0, S \to 1S1, S\to E, E \to \lambda, E\to 0, E\to 1$

Responder

Esta gramática define el conjunto de todas las cadenas sobre$B$ las cuales cada cadena es un palíndromo (la misma cadena si se lee hacia adelante o hacia atrás).

Ejercicio$\PageIndex{4}$

¿Qué conjuntos de cadenas están definidos por la siguiente gramática?

1. Símbolos terminales:$\lambda\text{,}$$a\text{,}$$b\text{,}$ y$c$
2. Símbolos no terminales:$S, T, U \textrm{ and } E$
3. Símbolo inicial:$S$
4. Reglas de producción:

\ begin {ecuation*}\ begin {array} {ccc} S\ a As & S\ a T & T\ a bT\\ T\ a U & U\ a Cu & U\ a E\\ & E\ a\ lambda &\\ end {array}\ end {ecuación*}

Ejercicio$\PageIndex{5}$

Defina los siguientes lenguajes$B$ con gramáticas de estructura de frases. ¿Cuáles de estos idiomas son regulares?

1. Las cadenas con un número impar de caracteres.
2. Las cuerdas de longitud 4 o menos.
3. Los palíndromos, cuerdas que son iguales hacia atrás que hacia adelante.

Responder

1. Símbolos de terminal: La cadena nula, 0 y 1. Símbolos no terminales: Símbolo$S\text{,}$$E\text{.}$ inicial: Reglas de$S\text{.}$ producción:$S\to 00S\text{,}$$S\to 01S\text{,}$$S\to 10S\text{,}$$S\to 11S\text{,}$$S\to E\text{,}$$E\to 0\text{,}$$E\to 1$ Esta es una gramática regular.
2. Símbolos de terminal: La cadena nula, 0 y 1. Símbolos no terminales: Símbolo$S\text{,}$$A\text{,}$$B\text{,}$$C$ inicial: Reglas de$S$ producción:$S \to 0A\text{,}$$S \to 1A\text{,}$$S \to \lambda$,$A \to 0B\text{,}$$A \to 1B\text{,}$$A \to \lambda\text{,}$$B \to 0C\text{,}$$B \to 1C\text{,}$$B \to A\text{,}$$C \to 0\text{,}$$C \to 1\text{,}$$C \to \lambda$ Esta es una gramática regular.
3. Ver Ejercicio$\PageIndex{3}$. Este lenguaje no es regular.

Ejercicio$\PageIndex{6}$

Defina los siguientes lenguajes$B$ con gramáticas de estructura de frases. ¿Cuáles de estos idiomas son regulares?

1. Las cuerdas con más 0's que 1's.
2. Las cuerdas con un número par de 1's.
3. Las cadenas para las que todos los 0 preceden a todos los 1.

Ejercicio$\PageIndex{7}$

Demostrar que si un lenguaje over$A$ es recursivo, entonces su complemento también es recursivo.

Responder

Si$s$ está en$A^*$ y$L$ es recursivo, podemos responder a la pregunta “Is s in$L^c\text{?}$” negando la respuesta a “Is$s$ in$L\text{?}$”

Ejercicio$\PageIndex{8}$

Usa BNF para definir las gramáticas en Ejercicios$\PageIndex{3}$ y$\PageIndex{4}$.

Ejercicio$\PageIndex{9}$

1. Demostrar que si$X_1, X_2, \ldots$ es una secuencia contable de conjuntos contables, la unión de estos conjuntos,$\underset{i=1}{\overset{\infty }{\cup}}X_i$ es contable.
2. Utilizando el hecho de que la unión contable de conjuntos contables es contable, demuestre que si$A$ es contable, entonces$A^*$ es contable.

Responder

1. Enumere los elementos de cada conjunto$X_i$ en una secuencia$x_{i1},\: x_{i2},\: x_{i3}\cdots$. Luego dibuja flechas como se muestra a continuación y enumere los elementos de la unión en orden establecido por este patrón:$x_{11}$,$x_{21}$,$x_{12}$,$x_{13}$,$x_{22}$,$x_{31}$,$x_{41}$,$x_{32}$,,$x_{23}$,$x_{14}$,$x_{15}\cdots$,
2. Cada uno de los conjuntos$A^{1}$$A^2$,,$A^{3},\cdots ,$ son contables y$A^∗$ es la unión de estos conjuntos; de ahí$A^∗$ es contable.

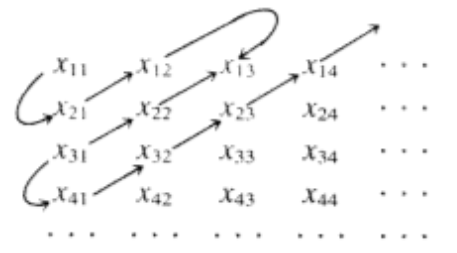Figura$\PageIndex{2}$: Ejercicio$\PageIndex{9}$