14.5: La máquina de un monoide

Última actualización
Guardar como PDF

Page ID: 117138

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Cualquier monoide finito se$[M;*]$ puede representar en forma de una máquina de estado finito con conjuntos de entrada y estado iguales a$M\text{.}$ La salida de la máquina se ignorará aquí, ya que haría eco del estado actual de la máquina. Las máquinas de este tipo se denominan máquinas estatales. Se puede demostrar que cualquier cosa que se pueda hacer con una máquina de estado finito se puede hacer con una máquina de estados; sin embargo, hay una compensación. Por lo general, las máquinas de estado que realizan una función específica son más complejas que las máquinas generales de estado finito.

Definición $\PageIndex{1}$: Machine of a Monoid

Si$[M;*]$ es un monoide finito, entonces la máquina de$M\text{,}$ denotado$m(M)\text{,}$ es la máquina de estado con conjunto de$M\text{,}$ entrada de estado establecido$M\text{,}$ y función de siguiente estado$t : M\times M \to M$ definida por$t(s, x) = s * x\text{.}$

Ejemplo$\PageIndex{1}$

Construiremos la máquina del monoide$\left[\mathbb{Z}_2;+_2\right]\text{.}$ Como se mencionó anteriormente, el conjunto de estados y el conjunto de entrada son ambos$\mathbb{Z}_2\text{.}$ La siguiente función de estado se define por$t(s, x) = s +_2 x\text{.}$ El diagrama de transición para$m\left(\mathbb{Z}_2\right)$ aparece en la Figura$\PageIndex{1}$. Observe cómo es idéntico al diagrama de transición del verificador de paridad, que tiene un monoide asociado que era isomórfico a$\left[\mathbb{Z}_2;+_2\right].$

$clipboard_eb6f73f09a57dc4e31cc62aa414f8f062.png$ Figura$\PageIndex{1}$: La máquina de$[\mathbb{Z}_2;+_{2}]$

Ejemplo$\PageIndex{2}$

El diagrama de transición de los monoides$\left[\mathbb{Z}_2;\times _2\right]$ y$\left[\mathbb{Z}_3;\times _3\right]$ aparecen en la Figura$\PageIndex{2}$.

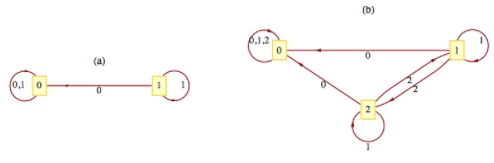$clipboard_ec12ddd668fd136247ffd94b51ad2f18b.png$ Figura$\PageIndex{2}$: Las máquinas de$[\mathbb{Z}_2;\times_{2}]$ y$\mathbb{Z}_{3};\times_{3}]$

Ejemplo$\PageIndex{3}$

Dejar$U$ ser el monoide que obtuvimos de la máquina de retardo de tiempo unitario (Ejemplo 14.4.2). Hemos visto que la máquina del monoide del verificador de paridad es esencialmente el verificador de paridad. Obtendremos una máquina de retardo de tiempo unitario cuando construimos la máquina de No$U\text{?}$ podemos esperar obtener exactamente la misma máquina porque la máquina de retardo de tiempo unitario no es una máquina de estados y la máquina de un monoide es una máquina de estados. No obstante, veremos que nuestra nueva máquina es capaz de decirnos qué entrada se recibió en el periodo de tiempo anterior. La tabla de operaciones para el monoide sirve como tabla para definir la función de transición para la máquina. Los encabezados de fila son los valores de estado, mientras que los encabezados de columna son las entradas. Si tuviéramos que dibujar un diagrama de transición con todas las entradas posibles, el diagrama sería demasiado difícil de leer. Ya que$U$ es generado por los dos elementos,$T_0$ y$T_1\text{,}$ vamos a incluir sólo esas entradas. Supongamos que queríamos leer la función de transición para la entrada$T_{01}\text{.}$ Desde$T_{01}=T_0T_1\text{,}$ en cualquier estado$s, t\left(s, T_{01}\right) = t\left(t\left(s, T_0\right), T_1\right).$ El diagrama de transición aparece en la Figura$\PageIndex{3}$.

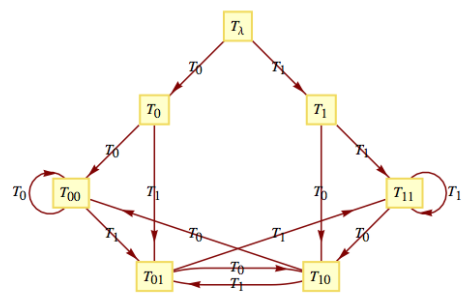$clipboard_e16231856685687ab526113b5e78ce41e.png$ Figura $\PageIndex{3}$: Copiar y Pegar Subtítulo aquí. (Copyright; autor vía fuente)

Si empezamos a leer una cadena de 0's y 1's mientras estamos en estado$T_{\lambda }$ y estamos en estado en cualquier$T_{ab}$ momento, la entrada del periodo de tiempo anterior (no la entrada que nos envió a$T_{ab}\text{,}$ la anterior) es$a\text{.}$ En estados$T_{\lambda }, T_0$ y$T_1\text{,}$ no existe ninguna entrada previa.

14.5.1: Ejercicios

Ejercicio$\PageIndex{1}$

Dibuje los diagramas de transición para las máquinas de los siguientes monoides:

$\displaystyle \left[\mathbb{Z}_4;+_4\right]$
El producto directo de$\left[\mathbb{Z}_2;\times _2\right]$ consigo mismo.

Contestar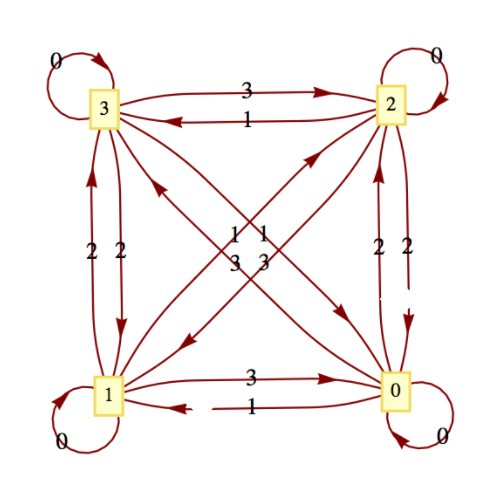: $clipboard_efac3272bb2625461e4f5a90e1b503441.png$ Figura$\PageIndex{4}$: (a)

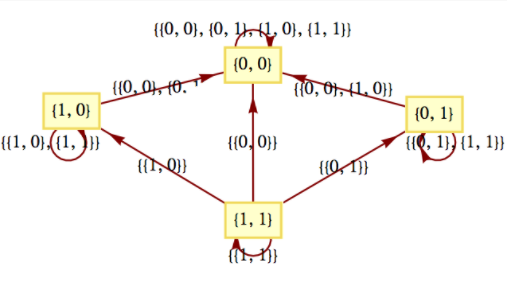$clipboard_e6777df5d4d0f344d5553f8f8a674111c.png$ Figura$\PageIndex{5}$: (b)

Ejercicio$\PageIndex{2}$

Aunque un monoide puede ser infinito, podemos visualizarlo como una máquina de estado infinito siempre que sea generado por un número finito de elementos. Por ejemplo, el monoide$B^*$ es generado por 0 y 1. Se puede obtener una sección de su diagrama de transición permitiendo la entrada solo desde el conjunto generador. El monoide de enteros en adición es generado por el conjunto$\{-1, 1\}\text{.}$ El diagrama de transición para este monoide se puede visualizar dibujando una pequeña porción del mismo, como en la Figura$\PageIndex{6}$. Lo mismo es cierto para el monoide aditivo de números enteros, como se ve en la Figura$\PageIndex{7}$.

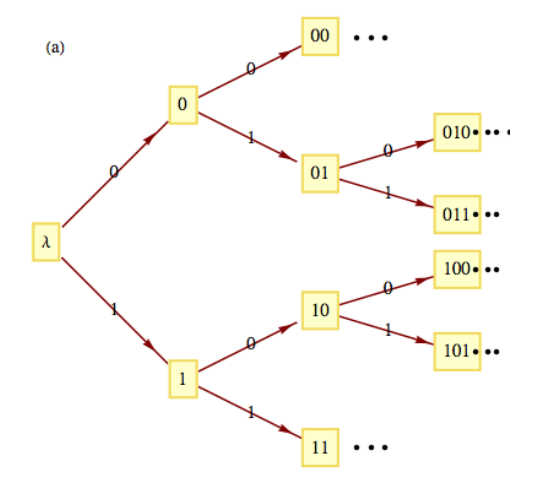$clipboard_e5e73a9006a935f62c7d27f55bfb9dd49.png$ Figura$\PageIndex{6}$: Una máquina infinita$B^*$

$clipboard_e4229df79efe29293f745684b410ab873.png$ Figura$\PageIndex{7}$: Una máquina infinita$[\mathbb{Z};+]$

Dibujar un diagrama de transición para$\{a, b, c\}$
Dibujar un diagrama de transición para$[\mathbb{Z}\times \mathbb{Z};\textrm{componentwise addition}]\text{.}$
Dibujar un diagrama de transición para$[\mathbb{Z};+]$ con conjunto generador$\{5,-2\}\text{.}$