1.13: Los enteros gaussianos
- Page ID
- 117461
En esta sección estudiamos un subconjunto especial de los números complejos conocidos como los enteros gaussianos.
Un entero gaussiano es un número complejo de la forma\(a+bi\) donde ambos\(a\) y\(b\) son números enteros. A menudo denotamos el conjunto de enteros gaussianos por\(\mathbb{Z}[i]\).
Para simplificar la notación (y no confundir enteros gaussianos con enteros ordinarios), a veces usaremos letras griegas\(\alpha, \beta\), etc. para representar enteros gaussianos.
Los enteros gaussianos tienen muchas propiedades especiales que son similares a las de los enteros. En este capítulo, una vez que tengamos algunos conceptos fundamentales, veremos cómo los enteros gaussianos satisfacen un algoritmo de división y una versión de factorización única. También veremos los enteros gaussianos aparecer algunas veces en capítulos posteriores.
Comenzamos con una representación gráfica. Así como los enteros forman puntos a lo largo de la línea real estándar,

podemos visualizar los enteros gaussianos como puntos espaciados regularmente, aunque en un nuevo contexto.
Los números complejos pueden ser representados por un dibujo bidimensional llamado plano Argand. Al igual que un plano cartesiano normal, un plano Argand contiene un eje horizontal y un eje vertical para las mediciones. Sin embargo, en lugar de representar un par ordenado de números reales, cada punto en el plano Argand representa un solo número complejo, el punto ubicado en lo que tradicionalmente se etiquetaría\((x,y)\) en coordenadas cartesianas representa el número complejo\(x+yi\), donde \(i\)es una raíz cuadrada de\(-1\), como de costumbre. Aquí se muestra una imagen del avión Argand:
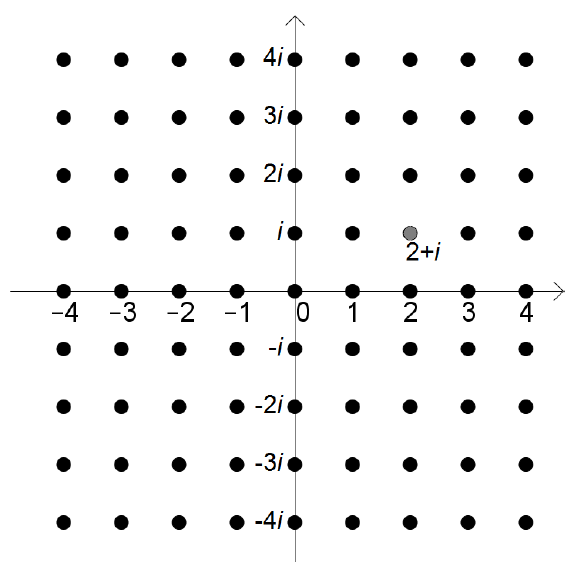
Los puntos sólidos marcan las ubicaciones de los enteros gaussianos. Tenga en cuenta que el eje horizontal mide la parte real de cada número complejo, y el eje vertical mide la parte imaginaria. De ahí que el punto\(2+i\) se ubica 2 unidades horizontalmente a la derecha del centro y una unidad verticalmente hacia arriba.
Dado que los enteros (reales) se encuentran en una sola línea, es fácil entender si un entero es “más grande” que otro. Para los enteros gaussianos, sin embargo, no está claro de inmediato si\(2+i\) es mayor o menor que 3. Porque poder comparar enteros gaussianos será importante para nosotros en breve, definiremos una manera de hacerlo.
La norma de un entero gaussiano\(\alpha = a+bi\), denotado\(N(\alpha)\) o\(N(a+bi)\), es un número real definido por\[N(\alpha) = N(a+bi)=a^2+b^2.\nonumber \]
Dado que la norma de un entero gaussiano es un número real, podemos usar normas para comparar “tamaños” de enteros gaussianos. Por ejemplo,\(N(2+i) = 5\) y\(N(3) = 9\) (desde\(3 = 3+0i\)), tan intuitivamente podemos pensar en\(2+i\) como menores que 3. En efecto, podrías notar que\(N(a+bi)\) es el cuadrado de la distancia habitual en línea recta de\(0\) a\(a+bi\) si pensamos en ellos como los puntos cartesianos\((0,0)\) y\((a,b)\). Por ejemplo\(1\),\(-1\),\(i\), y\(-i\) están cada una unidad de distancia de\(0\), y\(N(1)=N(-1)=N(i)=N(-i) = 1= 1^2\).
Una idea que quizás recuerdes de una exposición anterior a números complejos es la de un conjugado complejo.
Dado un número complejo\(\alpha=a+bi\), el conjugado (complejo) es el número complejo\(a-bi\), es decir, el número complejo obtenido cambiando el signo en la parte imaginaria. Denotamos el conjugado de\(\alpha\) con una barra horizontal por encima del número, entonces\(\overline{\alpha}=\overline{a+bi} = a-bi\).
Tenga en cuenta que\(\overline{a-bi} = a+bi\), también, por lo que el conjugado de un conjugado vuelve a ser el número complejo original. Obsérvese también que el conjugado de un número real es en sí mismo.
Algunas observaciones útiles conectan normas y conjugados. En lo siguiente, recuerde cómo se multiplican los números complejos:\[\begin{aligned} (a+bi)(c+di) &= ac + adi + bci + bdi^2\\ &= (ac-bd)+(ad+bc)i,\end{aligned}\] ya que\(i^2=-1\).
Para cualquiera\(\alpha \in \mathbb{Z}[i]\) tenemos lo siguiente:
- \(N(\alpha) = \alpha\cdot \overline{\alpha}\);
- \(N\left(\overline{\alpha}\right) = N(\alpha)\).
Prueba
Quizás la propiedad más importante sobre las normas es la siguiente.
[lem: normas multiplicativas] Para cualquier\(\alpha,\beta \in \mathbb{Z}[i]\),\[N\left(\alpha\beta\right) = N(\alpha)N(\beta).\nonumber \]
Prueba
Divisibilidad y división
Podemos hacer muchas de las mismas definiciones para enteros gaussianos que hemos hecho en capítulos anteriores para enteros.
Dados los enteros gaussianos\(\alpha\) y\(\beta\), diremos que\(\alpha\) divide\(\beta\) si existe otro entero gaussiano\(\gamma\) tal que\(\alpha \gamma = \beta\). En este caso llamamos\(\alpha\) un divisor de\(\beta\), y\(\beta\) un múltiplo de\(\alpha\).
Si\(p\) y\(q\) son enteros (reales), entonces se puede demostrar que\(p\) divide\(q\) bajo esta nueva definición de “divide” si y sólo si\(p|q\) como enteros.
Puede parecer un poco difícil al principio decidir si un entero gaussiano divide a otro. Por ejemplo, ¿cómo sabría si\(1-i\) divide 4, o si\(2+i\) divide 6? Como corolario de Lemma\(\PageIndex{2}\), podemos encontrar una manera rápida de descartar ciertas posibilidades.
Si\(N(\alpha)\) no divide\(N(\beta)\), entonces no\(\alpha\) es un divisor de\(\beta\).
Ya que\(N(2+i) = 5\)\(N(6)=36\) y y no\(5\) es un divisor de 36, sabemos que\(2+i\) no divide 6.
No obstante, ¿es\(1-i\) un divisor de 4? Comparando sus normas
\[\begin{gathered} N(1-i) = 1^2+(-1)^2 = 2,\\ N(4) = 4^2+0^2 = 16,\end{gathered}\]
sí vemos que\(2\) divide\(16\). Ni Corolario\(\PageIndex{1}\) ni Lema\(\PageIndex{2}\) garantizan eso\(1-i\) divide\(4\); todavía podría no hacerlo. Si lo hiciera, ¿cómo podríamos encontrar un número\(1-i\) por el que multiplicar para producir 4?
En este punto, aunque hemos tratado de evitar mucho uso de fracciones en este texto, nos resultará conveniente utilizarlas. El número que buscamos es\[\frac{4}{1-i},\nonumber \] pero este número complejo no está escrito en nuestra forma habitual de\(a+bi\); ¿cómo podemos ponerlo en esta forma?
Quizás recuerdes la respuesta de la experiencia pasada con números complejos: para poner una fracción compleja con un denominador no real en la forma\(a+bi\), multiplicamos tanto el numerador como el denominador por el conjugado del denominador.
En este caso, encontramos\[\frac{4}{1-i} = \frac{4}{1-i}\cdot \frac{1+i}{1+i} = \frac{4+4i}{1^2-i^2} = \frac{4}{2} + \frac{4i}{2} = 2 + 2i.\nonumber \]
Ya que\(2+2i\) es un entero gaussiano y\((1-i)(2+2i) = 4\), concluimos que sí,\(1-i\) es un divisor de\(4\). (Si el cociente hubiera resultado ser un número complejo distinto de un entero gaussiano, entonces habríamos llegado a la conclusión de que no\(1-i\) era un divisor).
Ahora que tenemos divisores definidos, necesitamos algunas definiciones más que no eran importantes a la hora de trabajar con enteros pero que serán útiles ahora.
Una unidad en\(\mathbb{Z}[i]\) es un elemento\(\omega\) para el cual\(N(\omega)=1\). Dos enteros gaussianos\(\alpha\) y\(\beta\) son asociados si existe una unidad\(\omega\) tal que\(\alpha \omega = \beta\).
Tenga en cuenta que si\(v+wi\) es una unidad en\(\mathbb{Z}[i]\), entonces\(v\) y\(w\) son enteros, y\(v^2+w^2 = 1\). La única forma en que esto puede suceder es si uno de\(v\) o\(w\) es\(\pm 1\) y el otro es 0. Así las únicas unidades en\(\mathbb{Z}[i]\) son\(1\),\(-1\),\(i\), y\(-i\). En consecuencia, cada unidad gaussiana tiene un total de cuatro asociados (contándose a sí misma).
El entero gaussiano\(2+3i\) tiene cuatro asociados: sí mismo, y\[\begin{aligned} (2+3i)(-1) &= -2-3i,\\ (2+3i)i &= -3 + 2i, \text{ and}\\ (2+3i)(-i) &= 3 - 2i.\end{aligned}\]
Los asociados juegan un papel importante en las declaraciones sobre la divisibilidad, por el siguiente lema.
Dejar\(\alpha\),\(\beta\), y\(\gamma\) ser enteros gaussianos.
- Si\(\alpha\) y\(\beta\) son asociados, entonces\(\gamma\) divide uno de\(\alpha,\beta\) si y sólo si divide al otro.
- Si\(\alpha\) y\(\beta\) son asociados, entonces\(\alpha\) divide\(\gamma\) si y sólo si\(\beta\) divide\(\gamma\).
Ahora, ¿qué podemos decir de los enteros gaussianos como\(2+i\) y\(6\) donde ninguno divide al otro? Como hicimos para los enteros, introducimos un teorema de tipo algoritmo de división para los enteros gaussianos.
Dados los enteros gaussianos\(\alpha\) y\(\beta\)\(\beta \neq 0\), donde, existen enteros gaussianos\(\kappa\) y\(\rho\) tales que\[\alpha = \beta\kappa+\rho \qquad \text{ and } \qquad 0 \leq N(\rho) < N(\beta).\nonumber \]
En aras de la brevedad, y debido a que los detalles son en algunos aspectos análogos a los de la prueba del Algoritmo de División, saltaremos la prueba del Teorema\(\PageIndex{1}\). No obstante, ilustraremos algunas de sus ideas en el siguiente ejemplo.
Vamos a encontrar\(\kappa\) y\(\rho\) dar\(\alpha = 6\) y\(\beta = 2+i\). Empezamos\(\kappa\) por computar el número complejo\[\frac{\alpha}{\beta}=\frac{6}{2+i} = \frac{6}{2+i}\cdot \frac{2-i}{2-i} = \frac{12-6i}{2^2 - (-1)^2} = \frac{12}{5} - \frac{6}{5}i.\nonumber \] La respuesta no es un entero gaussiano, como\(\kappa\) debería ser, por lo que redondearemos tanto la parte real como la imaginaria al entero más cercano y\(\kappa\) estableceremos igual al resultado, obteniendo aquí \(\kappa = 2 - i\).
Ahora nos encontramos con\(\rho = \alpha - \beta\kappa\):\[\rho = 6 - (2+i)(2-i) = 6 - 5 = 1.\nonumber \] Comprobamos que las normas funcionen como deberían, y vemos que efectivamente,\[0 \leq N(\rho) = N(1) = 1 < 5 = N(2+i) = N(\beta).\nonumber \]
En general, encontrar un cociente y un resto cuando un entero gaussiano se divide por otro se puede lograr tal como en el ejemplo anterior: tratamos los enteros gaussianos como números complejos y los dividimos como normales, produciendo un número complejo con coeficientes posiblemente no enteros para partes reales e imaginarias. Redondear estos números al entero más cercano proporcionará un cociente, que luego se puede usar para calcular el resto. Tenga en cuenta que a diferencia del Algoritmo de División, aquí no requerimos un resto no negativo, y no afirmamos que el cociente y el resto sean únicos. El siguiente ejemplo ilustra por qué.
Si intentamos encontrar un cociente y resto para los enteros gaussianos\(1+i\) y\(3i\) usando el mismo proceso que en el último ejemplo, encontramos\[\begin{gathered} 3i = (1+i)(2+2i) - i,\\ 0 \leq N(-i) < N(1+i); \end{gathered}\] o\[\begin{gathered} 3i = (1+i)(1+i) + i,\\ 0 \leq N(i) < N(1+i); \end{gathered}\] o tal vez\[\begin{gathered} 3i = (1+i)(1+2i) + 1,\\ 0 \leq N(1) < N(1+i);\\ \end{gathered}\] o\[\begin{gathered} 3i = (1+i)(2+i) - 1,\\ 0 \leq N(-1) < N(1+i); \end{gathered}\] desde en el primer paso cuando dividimos\(3i\) por \(1+i\)la fracción\(3i/(1+i)\) es igual a\(3/2 + (3/2)i\), y\(3/2\) es igualmente cercana a 1 y a 2.
Los mejores divisores comunes
Ahora que tenemos una versión entera gaussiana del Algoritmo de División, ¿podemos adaptar algunos de nuestros algoritmos anteriores, como el Algoritmo Euclidiana? ¿Qué nos diría el resultado? Vamos a intentarlo.
Si comenzamos el Algoritmo Euclideano con\(2-3i\) y\(3+5i\), podemos obtener\[\begin{aligned} 3+5i &= (2-3i)(-1+i) + 2;\\ 2-3i &= 2(1-2i) + i;\\ 2 &= i(-2i) + 0. \end{aligned}\] El último resto distinto de cero es\(i\).
Si los números involucrados en el Algoritmo Euclideano fueran enteros, interpretaríamos que el último resto distinto de cero es el mayor divisor común. ¿Podemos hacer lo mismo con los enteros gaussianos?
Sí, si tomamos el significado correcto para la palabra “mayor”. Como en la prueba del Algoritmo Euclidiana, un entero gaussiano es un divisor común de\(3+5i\) y\(2-3i\) si y solo si es un divisor común de\(2-3i\) y\(2\), lo que sucede si y solo si es un divisor común de\(2\) y\(i\), lo que ocurre si y sólo si es un divisor común de\(i\) y\(0\). Así todos los divisores comunes dividen\(i\), así\(i\) es el “mayor” divisor común en el sentido de que todo divisor común lo divide.
Por Lema\(\PageIndex{3}\), un entero gaussiano divide\(i\) si y solo si divide\(1\),\(-1\), o\(-i\), entonces estos cuatro asociados son todos los mayores divisores comunes de\(3+5i\) y \(2-3i\).
En general, llevar a cabo el Algoritmo Euclideano con enteros gaussianos siempre producirá un mayor divisor común, y podemos encontrar otros considerando asociados.
Factorización única
Estudiar los divisores de los enteros nos llevó a pensar en los números primos, aquellos enteros que no podían dividirse de manera uniforme por ningún número entero positivo menor que no sea 1. Luego vimos que cada entero positivo mayor que 1 podría escribirse de manera única como producto de estos primos, si ordenamos los primos de menor a mayor. Podemos estudiar preguntas similares para los enteros gaussianos, aunque las respuestas serán diferentes a veces.
Un elemento en\(\mathbb{Z}[i]\) se llama primo gaussiano si no puede escribirse como el producto de dos o más números gaussianos donde ninguno de los números del producto es una unidad.
Los números\(11-10i\) y no\(27\) son primos gaussianos, ya que\(11-10i=(2-3i)(4+i)\) y\(27 = 3\cdot 9=(3+0i)(9+0i)\).
En contraste,\(2+i\) es un primo gaussiano. Para ver por qué, supongamos al contrario eso\(2+i= \alpha\beta\), dónde\(\alpha,\beta \in \mathbb{Z}[i]\) y tampoco es una unidad. Por Lema\(\PageIndex{2}\),\[N(\alpha) N(\beta) = N(2+i) = 5.\nonumber \] Ya que\(N(\alpha)\) y\(N(\beta)\) son ambos enteros no negativos, uno debe ser igual a 5 y el otro debe ser igual a 1. No obstante, si cualquiera\(\alpha\) o\(\beta\) tiene una norma de 1 entonces es una unidad, contrario a nuestra suposición. Así\(2+i\) es un primo gaussiano.
Por el mismo razonamiento que en el ejemplo anterior, podemos decir lo siguiente.
Por cada\(\alpha \in \mathbb{Z}[i]\), si\(N(\alpha)\) es un número primo, entonces\(\alpha\) es un primo gaussiano.
Tenga en cuenta que lo contrario de Proposición\(\PageIndex{1}\) no es cierto; por ejemplo, la norma de\(3\) is\(9\), es compuesta, pero\(3\) sigue siendo un primo gaussiano (ver Ejercicio\(\PageIndex{6}\)).
El número 41 es un número primo; ¿también es un número primo gaussiano?
Si no, entonces existen enteros gassianos\(\alpha\) y\(\beta\) cuyo producto es 41, tal que ninguno es una unidad. Por Lema\(\PageIndex{2}\),\[N(\alpha) N(\beta) = N(41) = 41^2.\nonumber \] Esto obliga\(N(\alpha) = 41\) y\(N(\beta)=41\). ¿Podemos encontrar dos enteros gaussianos con norma 41 cuyo producto es 41?
¡Podemos! Observe eso\(4+5i\) y\(4-5i\) ambos tienen norma 41, y\((4+5i)(4-5i)=41\). De ahí que 41, aunque sea un número primo, no es un primo gaussiano.
Muchos otros números primos no son primos gaussianos (ver Ejercicio\(\PageIndex{6}\)), aunque algunos, como 3, son primos tanto en los enteros como en los enteros gaussianos. Podremos decir más sobre primos y primos gaussianos en los ejercicios de la Sección 1.28.
Ahora que tenemos la noción de primos gaussianos, ¿podemos factorizar los enteros gaussianos de manera única en primos gaussianos? A primera vista, la respuesta podría parecer no.
En el ejemplo anterior vimos que\[41 = (4+5i)(4-5i).\nonumber \] Desde\(N(4+5i)\) y\(N(4-5i)\) son números primos, sabemos por Proposición\(\PageIndex{1}\) que\(4+5i\) y\(4-5i\) son primos gaussianos.
Sin embargo, también podemos escribir\[41 = (5+4i)(5-4i),\nonumber \] y\(5+4i\) y también\(5-4i\) somos primos gaussianos. Esto significa que\(41\) no se puede escribir únicamente como un producto de primos gaussianos no unitarios.
Aún así, los números\(4\pm 5i\) y\(5\pm 4i\) están relacionados. Tenga en cuenta que\((4+5i)(-i) = 5-4i\)\((4-5i)i = 5+4i\), y, así\(4+5i\) y\(5-4i\) son asociados, como son\(4-5i\) y\(5+4i\). También podemos derivar una factorización de la otra:\[\begin{aligned} 41 &= (4+5i)(4-5i) \cdot 1\\ &= (4+5i)(4-5i) \cdot (-i)i\\ &= [(4+5i)(-i)][(4-5i)i]\\ &= (5-4i)(5+4i). \end{aligned}\] Porque\(-i\) y\(i\) multiplicar a 1, o porque\(4\pm 5i\) y\(5\mp 4i\) son asociados, ¿no podríamos decir que las dos factorizaciones son prácticamente las mismas?
De hecho, se puede demostrar que si\(\alpha\) es un primo gaussiano, entonces\(\omega\alpha\) es un primo gaussiano para cualquier unidad\(\omega\), así que al usar unidades cuyo producto es 1 como en el ejemplo anterior, podemos encontrar muchas factorizaciones de aspecto diferente de un entero gaussiano en Primos gaussianos.
Aún así, ¿y si relajamos nuestra noción de “similitud” en las factorizaciones para ignorar las diferencias en los asociados? Entonces los enteros gaussianos se pueden factorizar de manera única en primos gaussianos.
Cualquier entero gaussiano\(\alpha\) con una norma mayor que 1 se puede factorizar en primos gaussianos, y la factorización es única en el siguiente sentido: si\[\alpha = \beta_1\beta_2\cdots \beta_k= \gamma_1\gamma_2\cdots \gamma_\ell,\nonumber \] donde cada uno\(\beta_i\) y cada uno\(\gamma_i\) es un primo gaussiano, entonces\(k=\ell\) (es decir, el números de primos involucrados son los mismos) y los primos pueden ser reordenados y renumerados para que\(\beta_i\) sea un asociado de\(\gamma_i\) para todos\(i\).
No vamos a probar aquí este teorema, aunque se le anima a intentarlo. Demostrar la existencia de una factorización prime se puede hacer por inducción de la misma manera que usa Lemma 1.12.4; tratar de adaptar Lemma 1.12.5 para el resto.
Hemos visto cuántos de los resultados clave que hemos encontrado hasta ahora tienen análogos en el sistema numérico de los enteros gaussianos. Aunque a medida que avanza el texto, mencionaremos los enteros gaussianos solo unas cuantas veces más, se le invita a pensar en cómo se vería cada nuevo resultado si los enteros involucrados fueran reemplazados por enteros gaussianos. Hacerlo te llevará a preguntas de investigación; también puede darte una nueva perspectiva sobre cosas que ya conoces desde hace mucho tiempo.
Ejercicios
Demostrar ambas declaraciones en Lemma\(\PageIndex{1}\).
Demostrar ambas declaraciones en Lemma\(\PageIndex{3}\).
(Pista: Recordemos que las únicas unidades en\(\mathbb{Z}[i]\) son\(\pm 1\) y\(\pm i\).)
Escribir\(i\) como una combinación lineal de\(2-3i\) y\(3+5i\).
(Sugerencia: aplicar un método de la Sección 1.10 y quizás referirse a Ejemplo\(\PageIndex{5}\). Recuerde que los coeficientes sobre\(2-3i\) y\(3+5i\) deben ser enteros gaussianos; no pueden involucrar fracciones.)
Utilice el Algoritmo Euclidiana para encontrar un mayor divisor común de 5 y\(1-i\). Entonces escribe este mayor divisor común como una combinación lineal de\(5\) y\(1-i\).
(Sugerencia: Ver sugerencias del ejercicio anterior.)
- Demostrar que ninguno de\(2\)\(5\),\(13\),, o\(-3+4i\) es un primo gaussiano escribiendo cada uno como un producto de enteros gaussianos no unitarios.
(Pista:\(-3+4i\) es un cuadrado perfecto.) - Demostrar que\(3\) es un prime gaussiano.
(Sugerencia: supongamos que\(a+bi\) y\(c+di\) son enteros gaussianos no unitarios cuyo producto es 3, y concluimos que cada uno debe tener la norma 3; luego mostrar que ningún entero gaussiano tiene la norma 3.)
- Demostrar que\(1+i\) es un prime gaussiano.
- Demostrar que\(N(\alpha)\) es incluso si y solo si\(\alpha\) es un múltiplo de\(1+i\).
- Encuentra una factorización prima gaussiana de\(7+9i\). (Pista: hazte una idea de Ejercicio\(\PageIndex{7}\)).
- Encuentra al menos dos factorizaciones más de\(7+9i\) en primos gaussianos, para que no se repita ningún factor primo gaussiano entre las factorizaciones en la parte (a) y aquí.
El conjunto\(\mathbb{Z}[i]\) de enteros gaussianos es un sistema numérico que, al igual que\(\mathbb{Z}\), tiene factorizaciones únicas (hasta asociados). En este ejercicio consideraremos un sistema numérico ligeramente diferente.
Definir\[\mathbb{Z}[\sqrt{-5}] = \{a+b\sqrt{-5}\,\mid\, a,b \in \mathbb{Z}\}.\nonumber \] Resulta que si definimos una nueva norma por\(N(a+b\sqrt{-5}) = a^2+5b^2\), entonces\(N(\alpha\beta)=N(\alpha)N(\beta)\) por cada par de elementos\(\alpha,\beta \in \mathbb{Z}[\sqrt{-5}]\).
- Demostrar eso\(2\)\(23\),, y\(1+3\sqrt{-5}\) son todos “primos” en\(\mathbb{Z}[\sqrt{-5}]\), es decir, que no pueden escribirse como productos de factores que todos tienen normas menores.
(Pista: Utilizar la propiedad multiplicativa de la norma y una prueba por contradicción como en Ejemplo\(\PageIndex{6}\). Como parte de tu respuesta, demuestra que\(a^2+5b^2\) nunca es igual\(2\) o\(23\) cuando\(a\) y\(b\) son enteros.) - Demostrar que\(1+3\sqrt{-5}\) se divide\(46\) en\(\mathbb{Z}[\sqrt{-5}]\).
- Demostrar que\(\mathbb{Z}[\sqrt{-5}]\) no tiene una propiedad de factorización única.
(Pista: Mostrar que\(46\) no tiene una factorización única en los primos en\(\mathbb{Z}[\sqrt{-5}]\).)


